MATEMÁTICAS

GRADO 9 - PERIODO 2

DBA 2. Propone y desarrolla expresiones algebraicas en el conjunto de los números reales y utiliza las propiedades de la igualdad y de orden para determinar el conjunto solución de relaciones entre tales expresiones 

ESTANDAR BÁSICO DE COMPETENCIA: 

• Identifico relaciones entre propiedades de las gráficas y propiedades de las ecuaciones algebraicas.

• Construyo expresiones algebraicas equivalentes a una expresión algebraica dada.

TEMAS: 1. Factorización (Factor común, factor común por agrupación de términos, trinomio cuadrado perfecto (TCP), diferencia de cuadrados, trinomio cuadrado perfecto por adición y sustracción, trinomio de la forma x^2+bx+c, trinomio de la forma ax^2+bx+c, cubo perfecto de binomios, suma o diferencia de cubos perfectos, suma o diferencia de dos potencias iguales, 

Conocimientos previos: Números primos y compuestos

En matemáticas, un número primo es un número natural mayor que 1 que tiene únicamente dos divisores positivos distintos: él mismo y el 1 (la unidad).​ Por el contrario, los números compuestos son los números naturales que tienen algún divisor natural aparte de sí mismos y del 1, y, por lo tanto, pueden factorizarse. 

Para entender mejor este concepto, te invito a observar el siguiente video:

1. FACTORIZACIÓN

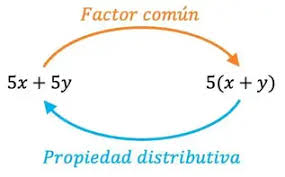
Factorizar una expresión algebraica consiste en escribirla como un producto (multiplicación). Luego entonces, hallar el producto y descomponerlo en factores primos son dos procesos inversos. 

Cuando factorizamos, debemos entender que la descomposición que se efectúa debe ser la más completa posible, es decir, hasta que todos sus factores sean primos entre sí. 

PRUEBA GENERAL DE LOS FACTORES: En todos los casos de factorización que verás, la prueba general de los factores, consiste en multiplicar los factores primos que se obtienen, y ese producto tiene que ser igual ala expresión factorizada. Esta prueba funciona como comprobación de la factorización.

1. FACTOR COMÚN MONOMIO

Existe factor común cuando una misma cantidad (número y/o letra) está presente en todos los términos de la expresión a factorizar. Para obtener el factor común monomio debemos seguir los siguientes pasos: 

1. Extraer el factor común numérico (MCD: máximo común divisor de los coeficientes) 

2. Extraer el factor común literal (MCD: variable que está en todos los términos del polinomio con el menor exponente entre ellos).

De 1 y 2 se obtiene el factor común monomio.

3. Ahora procedemos a dividir cada término del polinomio a factorizar entre el factor común calculado, y se escribe como el producto de dos factores. El primero, será el factor común obtenido y el segundo serán los cocientes obtenidos, separados por los signos del polinomio.

Ejemplo 1:

Descomponer en factores primos: ax - bx

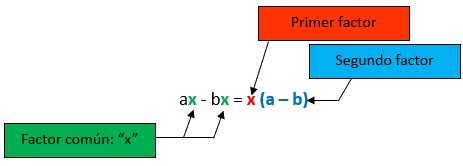
Ejemplo 2:

Si no te quedó claro el tema te invito a observar el siguiente video:

o este otro:

https://pruebat.org/Aprende/Materiales/verRecurso/44341/b42b3d9caa4b4d0bc1d44c99d8feca89/406110/1-2   

Te invito a practicar jugando en el siguiente link:

https://wordwall.net/es/resource/20650978/factorizaci%C3%B3n-factor-com%C3%BAn-identifica-el-factor-com%C3%BAn 

o haciendo clic en la imagen:

ACTIVIDAD 1: 

1. Ahora inténtalo tú en el cuaderno completando la factorización:

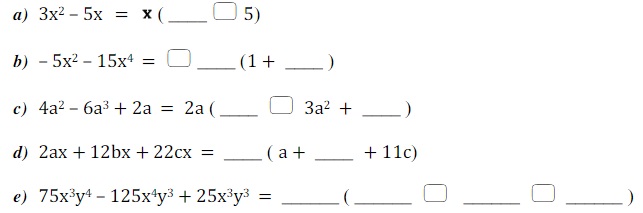
2. Realizar las 7 preguntas del link de Khan Academy y le enseñas el resultado al docente de aula:

https://es.khanacademy.org/math/algebra2/x2ec2f6f830c9fb89:poly-factor/x2ec2f6f830c9fb89:mono-factor/a/factoring-monomials 

2. FACTOR COMÚN POLINOMIO

Para factorizar un polinomio en que el factor común es otro polinomio, el procedimiento es similar al aplicado para el factor común monomio, excepto que en este caso el factor común será un polinomio. En algunos casos será necesario ordenar y/o agrupar términos 

Ejercicio 2: Ahora Intenta completar la siguiente expresión en tu cuaderno:

Afianza tu conocimiento sobre el tema observando el siguiente video:

ACTIVIDAD 2

EJERCICIOS FINALES DE MONOMIOS Y POLINOMIOS PARA REALIZAR EN EL CUADERNO (AFIANZAMIENTO)

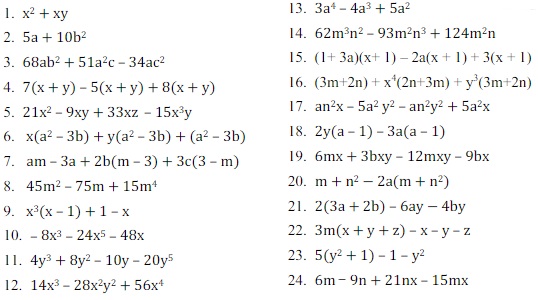
3. FACTOR COMÚN POR AGRUPACIÓN DE TÉRMINOS

Cuando no todos los términos de una expresión algebraica tienen un mismo factor común podemos utilizar la agrupación de términos; lo cual consiste en agrupar igual cantidad de términos en paréntesis, separados por el signo de más, de tal forma que cada paréntesis contenga un factor común. Luego aplicamos la factorización por factor común en cada uno de los paréntesis, y posteriormente, si es posible, aplicamos el factor común polinomio. 

Ejemplos: Descomponer utilizando el factor común por agrupación de términos: 

En ocasiones es posible efectuar otro tipo de asociación de términos y de igual manera se llega a la respuesta. Resolvamos el ejercicio anterior efectuando otro tipo de agrupación 

Te invito a observar los siguiente videos:

ACTIVIDAD 3.

1. Ahora intenta completar en tu cuaderno la factorización de estos polinomios:  

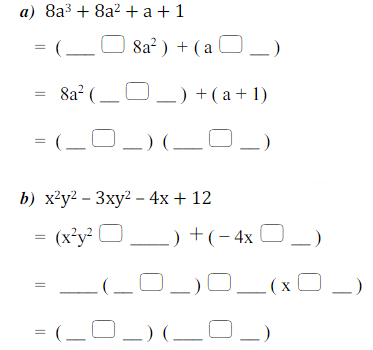
2. En el siguiente listado de expresiones algebraicas, clasifique las mismas en Factor Común Monomio, Factor Común Polinomio o Factor Común por Agrupación. Coloque A, B o C como sea el caso 

3. Realiza ejercicios a través del juego en el siguiente enlace:

https://www.cerebriti.com/juegos-de-matematicas/identifica-el-caso-de-factorizacion 

4. TRINOMIO CUADRADO PERFECTO

Se identifica por tener tres términos, de los cuales dos tienen raíces exactas, y el restante equivale al doble producto de las raíces. Un trinomio cuadrado perfecto es el desarrollo de un un binomio al cuadrado. Para solucionar un Trinomio cuadrado perfecto debemos: 

1. organizar los términos dejando de primero y de tercero los términos que tengan raíz cuadrada. 

2. extraemos la raíz cuadrada del primer y tercer término y los escribimos en un paréntesis, separándolos por el signo que acompaña al segundo término. 

3. el paréntesis elevamos todo el binomio al cuadrado. 

EJEMPLO1:

EJEMPLO2:

Te invito a observar el siguiente video para afianzar el tema:

Practica jugando:

https://wordwall.net/es/resource/11150846/trinomio-cuadrado-perfecto 

ACTIVIDAD 4.

1. Gamificación: Visita el siguiente link y desarrolla los ejercicios que allí aparecen:

https://wordwall.net/es/resource/11010922/trinomio-cuadrado-perfecto 

Luego envíale el pantallazo de tus resultados al docente

2. Práctica: Realiza los siguientes ejercicios en el cuaderno:

5. DIFERENCIA DE CUADRADOS

Se identifica por tener dos términos elevados al cuadrado y unidos por el signo menos. Se resuelve por medio de dos paréntesis (parecido a los productos de la forma uno positivo y otro negativo). En los paréntesis deben colocarse las raíces. 

EJEMPLOS:

Observa el siguiente video para reforzar el tema:

Ahora practica jugando:

https://wordwall.net/es/resource/4190703/diferencia-de-cuadrados 

ACTIVIDAD 5

1. Gamificación: Visita el siguiente link y desarrolla los ejercicios que allí aparecen:

https://wordwall.net/es/resource/11010922/trinomio-cuadrado-perfecto 

Luego envíale el pantallazo de tus resultados al docente

2. Práctica: Descarga o imprime el siguiente archivo y realiza sus ejercicios :

3. Resuelve: 

6. TRINOMIO CUADRADO PERFECTO POR ADICIÓN Y SUSTRACCIÓN

Existen algunos trinomios, en los cuales su primer y tercer términos son cuadrados perfectos (tienen raíz cuadrada exacta), pero su segundo términos no es el doble producto de sus raíces cuadradas.

x^2 + 2x + 9, no es un trinomio cuadrado perfecto. 

Para que un trinomio de estos se convierta en un trinomio cuadrado perfecto, se debe sumar y restar un mismo número (semejante al segundo término) para que el segundo término sea el doble producto de las raíces cuadradas del primer y último término. A este proceso se le denomina completar cuadrados. 

Ejemplo1:

Ejemplo2:

Te invito a reforzar el tema observando los siguientes videos:

Actividad 6: 

TRINOMIO DE LA FORMA X^2 + bX + c 

Los trinomios de esta forma tienen las siguientes características: 

1. El coeficiente del primer término es 1. 

2. La variable del segundo término es la misma que la del primer término pero con exponente a la mitad. 

3. El tercer término es independiente de la letra que aparece en el primer y segundo términos del trinomio.

Esto quiere decir, que la suma o resta de estos dos números sea igual al coeficiente del segundo término y su producto sea el tercer término; los signos de los factores son: en el primer factor se escribe el signo del segundo término del trinomio y para el segundo factor se multiplican el signo del segundo término con el signo del tercer término. 

Ejemplos:

Actividad 7: 

Cubo perfecto de binomios

Su forma desarrollada es un cuatrinomio (polinomio de cuatro términos) que obedece a la estructura: 

Una expresión algebraica ordenada con respecto a una letra es un cubo perfecto, si cumple las siguientes condiciones: 

1. Tener cuatro términos 

2. El primer y último término sean cubos perfectos (tienen raíz cúbica exacta). 

3. El segundo término es tres veces el producto del cuadrado de la raíz cúbica del primer término por la raíz cúbica del último término. 

4. El tercer término sea tres veces, el producto de la raíz del primer término por el cuadrado de la raíz del último término. 

5. El primer y tercer términos son positivos, el segundo y el cuarto términos tienen el mismo signo (positivo o negativo). Si todos los términos son positivos, el polinomio dado es el cubo de la suma de las raíces cúbicas del primer y último término. Y si los términos son alternadamente positivos y negativos el polinomio dado es el cubo de la diferencia de las raíces 

RECUERDA: La raíz cúbica de un monomio se obtiene extrayendo la raíz cúbica de su coeficiente y dividiendo el exponente de cada letra entre 3. 

Ejemplo2:

Ejemplo3:

Ejemplo4:

Ejemplo5:

Ejemplo6:

Te invito a observar el siguiente video sobre el tema:

Te invito a que practiques jugando:

https://wordwall.net/es/resource/32740579/cubo-de-un-binomio 

Actividad 9:

Realiza en tu cuaderno los siguientes ejercicios:

SUMA Y DIFERENCIA DE CUBOS PERFECTOS

La suma y la diferencia de cubos perfectos son casos especiales de factorización que permiten simplificar expresiones algebraicas y resolver ecuaciones de forma más rápida. Un cubo perfecto es un número o expresión que puede escribirse como algo elevado a la tercera potencia, por ejemplo: a³, 8 = 2³, 27x³ = (3x)³. Reconocer estos patrones es clave para aplicar correctamente las fórmulas y evitar errores de signo.

Fórmulas básicas

• Suma de cubos: a³ + b³ = (a + b)(a² − ab + b²)
• Diferencia de cubos: a³ − b³ = (a − b)(a² + ab + b²)

Observa que en ambos casos el primer paréntesis conserva las raíces cúbicas (a ± b) y el segundo paréntesis siempre tiene tres términos con cuadrados y producto, pero con signos diferentes según sea suma o diferencia.

Cómo identificar cubos perfectos

Para aplicar estas fórmulas, primero debes reconocer si cada término es un cubo perfecto:

• Revisa si el número tiene raíz cúbica exacta: 1, 8, 27, 64, 125, 216, 343, 512, 729…
• Verifica si las variables tienen exponente múltiplo de 3: x³, y⁶, a⁹, etc.
• Escribe cada término como potencia de exponente 3: por ejemplo, 8x³ = (2x)³, 27y³ = (3y)³.

Una vez que expresas cada término como a³ y b³, puedes identificar si se trata de una suma (a³ + b³) o una diferencia (a³ − b³) y aplicar la fórmula correspondiente.

Ejemplos resueltos: suma de cubos

Ejemplo 1: Factoriza 8x³ + 27

1. Identificamos cubos perfectos:
8x³ = (2x)³ y 27 = 3³, por lo tanto a = 2x y b = 3.

2. Aplicamos la fórmula a³ + b³ = (a + b)(a² − ab + b²):

8x³ + 27 = (2x)³ + 3³ = (2x + 3)( (2x)² − (2x)(3) + 3² )

= (2x + 3)(4x² − 6x + 9)

Ejemplo 2: Factoriza x³ + 64

x³ + 64 = x³ + 4³, entonces a = x y b = 4:

x³ + 64 = (x + 4)(x² − 4x + 16)

Ejemplos resueltos: diferencia de cubos

Ejemplo 3: Factoriza 27y³ − 8

1. Identificamos cubos perfectos:
27y³ = (3y)³ y 8 = 2³, por lo tanto a = 3y y b = 2.

2. Aplicamos la fórmula a³ − b³ = (a − b)(a² + ab + b²):

27y³ − 8 = (3y)³ − 2³ = (3y − 2)( (3y)² + (3y)(2) + 2² )

= (3y − 2)(9y² + 6y + 4)

Ejemplo 4: Factoriza x³ − 125

x³ − 125 = x³ − 5³, entonces a = x y b = 5:

x³ − 125 = (x − 5)(x² + 5x + 25)

Aplicaciones y representación visual

La suma y diferencia de cubos aparecen en problemas de geometría (volúmenes de cubos y prismas), en ecuaciones polinómicas y en simplificación de expresiones algebraicas complejas. Visualmente, un cubo perfecto representa el volumen de un cubo de lado a, es decir, a³. La suma de cubos puede interpretarse como la combinación de dos volúmenes cúbicos, mientras que la diferencia de cubos representa el volumen que queda al retirar un cubo más pequeño de uno mayor.

En videos educativos suele mostrarse cómo se descompone un cubo en partes más pequeñas para ilustrar por qué las fórmulas tienen esos términos y signos. Estos recursos visuales ayudan a entender que no son reglas arbitrarias, sino que tienen una base geométrica.

Ideas de videos para reforzar el tema

Aunque aquí no se insertan videos directamente, puedes buscar y trabajar con los siguientes tipos de recursos audiovisuales:

Explicación paso a paso de las fórmulas de suma y diferencia de cubos con animaciones geométricas.

Ejercicios resueltos de factorizar expresiones como 8x³ + 27, x³ − 64, 125a³ + 1, etc.

Aplicaciones en problemas de volumen y en resolución de ecuaciones cúbicas sencillas.

Actividad 10:

A continuación, se proponen actividades para reforzar el aprendizaje de la suma y diferencia de cubos perfectos. Puedes resolverlas en tu cuaderno o utilizarlas como guía para una ficha de trabajo.

1. Identificación de cubos perfectos

• Indica cuáles de las siguientes expresiones son cubos perfectos y escribe su raíz cúbica: 8x³, 16y³, 27a³, 64, 125m³, 9z³.

2. Factorización directa

• Factoriza usando suma de cubos: 
• a) x³ + 1
• b) 8y³ + 27
• c) 125a³ + 8.
• Factoriza usando diferencia de cubos: 
• a) x³ − 8
• b) 27m³ − 1
• c) 64p³ − 125.

Más actividades y retos

3. Ecuaciones con suma y diferencia de cubos

• Resuelve las ecuaciones factorizando primero:
  a) x³ − 8 = 0
  b) 8x³ + 27 = 0
  c) 27y³ − 1 = 0

4. Problemas de aplicación

• Un cubo de lado 3 cm se coloca junto a otro de lado 2 cm. Expresa la suma de sus volúmenes como suma de cubos y factorízala.
• De un cubo de lado 5 cm se extrae un cubo de lado 3 cm. Expresa el volumen restante como diferencia de cubos y factorízala.

5. Crea tus propios ejemplos

• Diseña 3 expresiones que sean suma de cubos y 3 que sean diferencia de cubos. Intercámbialas con un compañero para que las factorice.

Al finalizar, revisa tus resultados comparándolos con las fórmulas y corrige cualquier error de signo o de cálculo.