Grado 9

ESTADÍSTICA - PERIODO2

Logro:  Reconozco tendencias que se presentan en conjuntos de variables relacionadas

Estándar Básico de competencia: Interpreto nociones básicas relacionadas con el manejo de información como población, muestra, variable aleatoria, distribución de frecuencias, parámetros y estadígrafos).

1. VARIABLES CUANTITATIVAS Y VARIABLES CUALITATIVAS

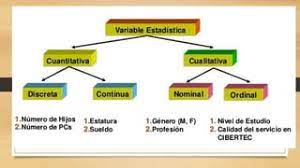
Una variable es una característica que al medirse en diferentes individuos puede tomar diferentes valores.

Por ejemplo, cuando preguntamos a los estudiantes de primaria cuál deporte es su preferido entre futbol y saltar la cuerda, la respuesta puede ser muy variada, ya que a los niños de menor edad les gustará más saltar la cuerda y a los niños de mayor edad les gustará más el futbol.

También podemos tener en cuenta que a las niñas les gustará más saltar la cuerda y a los niños el futbol.

Entonces podemos decir que para realizar esta encuesta debemos tener en cuenta dos variables:

VARIABLE 1: LA EDAD DE LOS ESTUDIANTES

VARIABLE 2: EL GÉNERO O SEXO DE LOS ESTUDIANTES.

TIPOS DE VARIABLE:

1. VARIABLES CUALITATIVAS: son aquellas que expresan características o cualidades.

Por ejemplo:

• El deporte favorito
• El lugar de nacimiento
• El color del cabello
• La comida favorita

2. VARIABLES CUANTITATIVAS: Son aquellas que se expresan mediante números, es decir, se pueden contar.

Por ejemplo:

• La edad de los estudiantes de un curso.
• La hora de acostarse de los estudiantes de quinto.
• La cantidad de juguetes que tiene un niño.
• El tiempo que tarda una pastilla efervescente en disolverse.

ACTIVIDAD 1

Los estudiantes del grado quinto se reunieron en tres grupos y realizaron encuestas con las preguntas de las tablas y obtuvieron estos resultados:

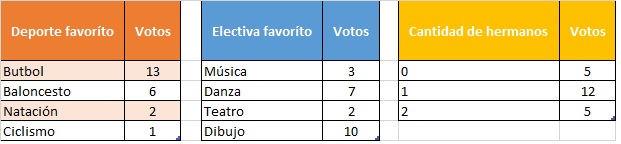
Responde en tu cuaderno:

a. ¿cuál o cuáles grupos realizaron la encuesta con una variable cuantitativa? ____________________

b. ¿cuál o cuáles grupos realizaron la encuesta con una variable cualitativa? ______________________

c. ¿A cuántos estudiantes se les aplicó la encuesta en el grupo 1? ______________________________

d. ¿A cuántos estudiantes se les aplicó la encuesta en el grupo 2? ______________________________

e. ¿A cuántos estudiantes se les aplicó la encuesta en el grupo 3? ______________________________

f. Realiza la gráfica de barras con los resultados del grupo 2:

2. FRECUENCIAS

Cuando se han recopilado datos de una muestra, éstos normalmente se encuentran desordenados, para proceder a analizarlos estadísticamente es necesario agruparlos en orden creciente o decreciente, si se trata de variables cuantitativas.

Es importante considerar algunos conceptos:

RANGO: Es la diferencia entre el dato mayor y el dato menor.

FRECUENCIA ABSOLUTA (fi): El número de veces que se presenta un dato. Ej: cantidad de estudiantes que sacaron notas de 1 a 10 del periodo 2 de matemáticas

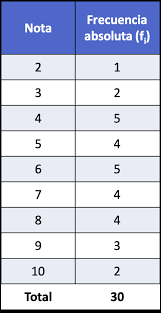
FRECUENCIA ABSOLUTA ACUMULADA (F): Es el número de observaciones menor o igual al

valor considerado. Se obtiene sumando sucesivamente las frecuencias absolutas.

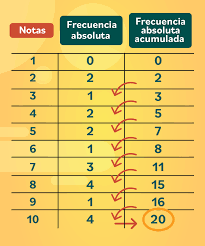
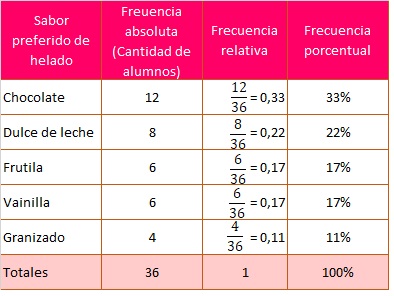
FRECUENCIA RELATIVA (hi): Es el cociente entre la frecuencia absoluta y la cantidad

total de datos (frecuencia total). Al multiplicar por 100 cada frecuencia relativa se obtiene la frecuencia porcentual.

FRECUENCIA PORCENTUAL (%)

Se puede calcular rápidamente multiplicando la frecuencia relativa por 100%

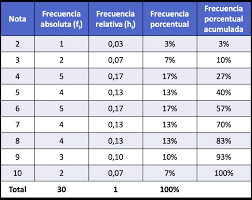
FRECUENCIA PORCENTUAL ACUMULADA

Se obtiene sumando sucesivamente la frecuencia porcentual acumulada

EJEMPLO:

A un grupo de jóvenes se les consulta por el número de hermanos que tiene cada uno, las respuestas están registradas en la siguiente tabla:

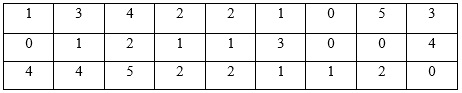
Con los datos, se construye la tabla de frecuencia: 

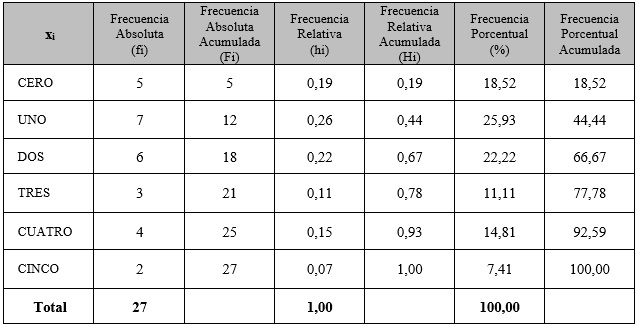
Sino entendiste muy bien el tema te invito a reforzarlo viendo este video:

ACTIVIDAD 2

En un colegio, se toma la estatura de 80 alumnos al azar dando los siguientes resultados: 

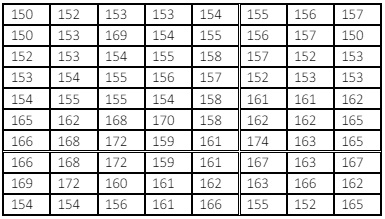
Realizar la tabla de frecuencia para estos datos de acuerdo al ejemplo anterior. Debe ser enviado via wp o correo al docente.

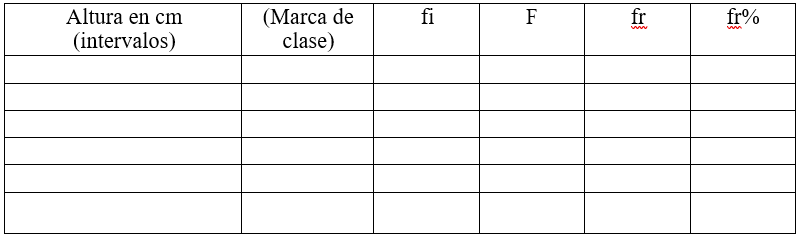
Amplitud de la clase:

La amplitud de la clase es la diferencia entre el límite superior e inferior de la clase.

Marca de clase:

La marca de clase es el punto medio de cada intervalo y es el valor que representa a todo el intervalo para el cálculo de algunos parámetros (xi)

Para determinar los intervalos de una distribución de frecuencias, es necesario seguir los siguientes pasos.

1. Determinar el RANGO; se refiere a la diferencia entre el mayor y el menor de la variable.
2. Determinar el número de intervalos. Se refiere a la cantidad de intervalos de clases en los cuales se agruparán los datos. La cantidad es arbitraria, aunque generalmente se usan 10 ó un número cercano a 10. Al elegir muchos intervalos (más de 25), es poco lo que se gana con la agrupación y al elegir pocos intervalos (menos de 5) se pierde parte de la información o se distorsiona.
3. Determinar el Tamaño de los Intervalos, se refiere al cociente entre el Rango y el Número de Intervalos que se quiera obtener.
4. Fijar el Límite Inferior y Superior de cada intervalo. Con esto se obtienen intervalos "cerrados – abiertos", es decir, un dato igual al Límite superior de un intervalo corresponderá al intervalo siguiente. 
5. Para obtener los intervalos se comienza por el mínimo valor de la variable u otro que estimemos pertinente, que será el extremo inferior del primer intervalo, se suma a este valor la amplitud para obtener el extremo superior y así sucesivamente. Se forman los intervalos teniendo presente que el límite inferior de una clase pertenece al intervalo, pero el límite superior no pertenece al intervalo y se cuenta en el siguiente intervalo.
6. Determinar la Marca de Clase y Completar la Tabla de Frecuencias Relativas y Acumuladas, con sus Porcentajes.

Nota: Si el tamaño del intervalo no resulta ser un número entero (en algunos casos), si la variable es cuantitativa discreta, conviene aproximarlo al entero que corresponda.

EJEMPLO:

Construye la tabla de frecuencias para las notas de una prueba de las 44 alumnas de un curso, agrupándolos en seis intervalos.

El resultado será el siguiente:

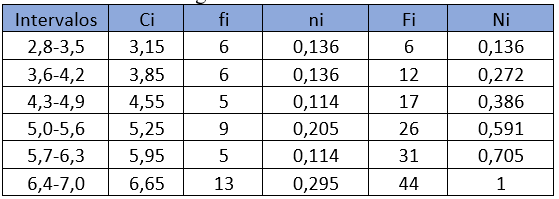
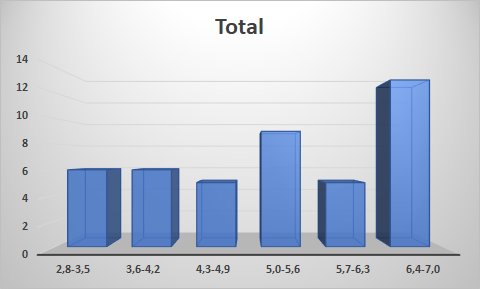
EJERCICIOS:

1. En la siguiente tabla se presentan los gustos musicales de los alumnos de primer año medio.

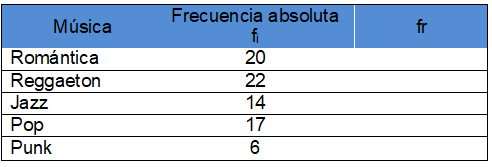
Calcule la frecuencia relativa de cada tipo de música.

2. Para la elección de presidente de curso se presentan Ana, José, Ema y Juan. Las votaciones son las siguientes:

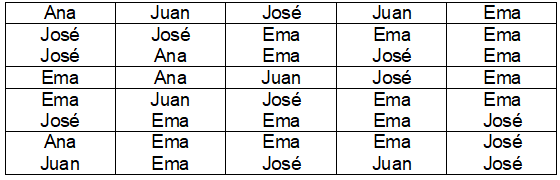
a. Construya una tabla de frecuencias absolutas y relativas.

b. En la votación de presidente de curso, ¿qué porcentaje obtuvo cada candidato?

3. Se encuestó a 54 familias de un determinado grupo socioeconómico, sobre su gasto mensual en calefacción. Las respuestas obtenidas, en miles de pesos, son las siguientes.

12 – 26 – 31 – 11 – 45 – 11 – 16 – 35 – 23 – 46 – 28 – 50 – 13 – 38 – 32 – 28 – 34 – 19

21 – 35 – 41 – 13 – 16 – 24 – 28 – 32 – 42 – 14 – 17 – 22 – 37 – 18 – 15 – 23 – 27 – 31

10 – 23 – 35 – 12 – 14 – 29 – 33 – 27 – 32 – 19 – 31 – 28 – 17 – 36 – 41 – 38 – 20 – 28

a) Organizar los datos entregados en una tabla de frecuencia para datos agrupados, distribuyéndolos en intervalos de amplitud 5.

b) La tabla de frecuencias solicitada debe contener las mismas columnas del ejercicio anterior.

4. En un centro comercial, se consultó la edad a todas las personas que entraban entre las 12:00 h y 12:30 horas. Los resultados obtenidos fueron los siguientes:

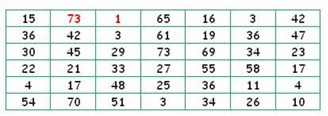
Construir una tabla de frecuencias cuyos datos estén agrupados en ocho intervalos.

5. En la clase de Educación Física se ha medido la altura de los alumnos con el fin de determinar si el peso está de acuerdo con la estatura de cada uno. Los datos en metros son los siguientes:

En este caso, por tratarse de una variable cuantitativa continua, se ha decidido agrupar los datos en intervalos.

a) Complete la tabla: