Grado 8 - Periodo 3
Matemáticas
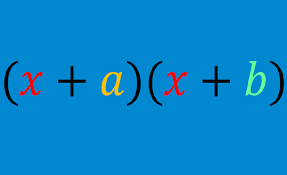
TEMA: ProporcionalidadFactorización
1- factorización (expresiones algebraicas), 2-Factorización (factor común monomio, agrupación de términos, 3-Factorización de binomios (diferencia de cuadrados, cubo perfecto de binomio), 4-trinomio cuadrado perfecto, diferencia de cuadrado perfecto. 5-Factorización de polinomios, 6-Aplicaciones de factorización, 7-Fracciones algebraicas
DBA9. Propone, compara y usa procedimientos inductivos y lenguaje algebraico
para formular y poner a prueba conjeturas en diversas situaciones o contextos.
ESTANDAR BÁSICO DE COMPETENCIA:
Construyo expresiones algebraicas equivalentes a una expresión algebraica dada.
Modelo situaciones de variación con funciones polinómicas.
CONOCIMIENTOS PREVIOS:
1. MCD (Máximo Común Divisor)
Para recordar el tema te invito a observar el siguiente video:
2. Leyes de los exponentes:
FACTORIZACIÓN
1. EXPRESIONES ALGEBRAICAS

Es una combinación de cantidades numéricas y literales, relacionadas por las operaciones de suma, resta, multiplicación, división, potenciación y radicación. Las letras reciben el nombre de variables .
Ejemplo:
Las siguientes expresiones son algebraicas:
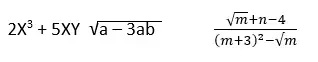
1.1. Tipos de expresiones algebraicas:
a. Expresiones algebraicas enteras: En ellas intervienen las operaciones básicas y los exponentes de las variables son números enteros positivos.
b. Expresiones algebraicas fraccionarias: Tienen algunas variables en el denominador.
Ejemplo:

C. Expresiones algebraicas irracionales: Contienen expresiones radicales en sus términos o variables con exponente racional no entero
Ejemplo:
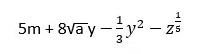
1.2. Valor numérico de una expresión algebraica
Es el resultado que se obtiene de sustituir la parte literal de la expresión algebraica por números determinados y aplicar las operaciones indicadas en la expresión.
Ejemplo:

Sino te quedó claro el tema observa el siguiente video:
Actividad 1
1. Escriba las expresiones algebraicas correspondientes a cada uno de los anunciados:

2. Determinar el valor numérico de las siguientes expresiones algebraicas sabiendo que:
x = -2, y = 3, z = 4
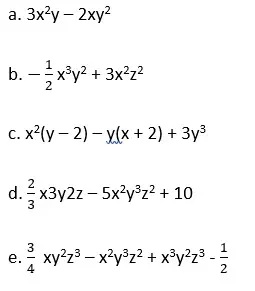
3. La energía potencial está dada por la expresión Ep = mgh, donde m es la masa, g es la gravedad (g=9,8 m/s2) y h la altura
Según esta información completa la tabla

4. Ve al siguiente link y realizar el juego en linea y al terminar envía el pantallazo al docente:
https://www.cerebriti.com/juegos-de-matematicas/o-expresiones-algebraicas
2. MONOMINO
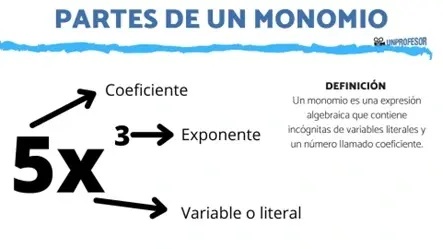
Es una expresión algebraica que consta de un solo término, formado por el producto de números reales y las potencias de exponente entero positivo de una o más variables.
2.1. Elementos de un monomio
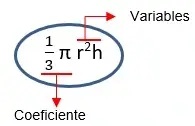
Un monomio está formado por:
- Un coeficiente, que es la parte numérica
- Una parte literal o variable, constituida por las variables y sus exponentes naturales.

El grado absoluto de un monomio corresponde a la suma de todos los exponentes de las variables.

Si dos o más monomios tienen el mismo grado absoluto, son homogéneos. De lo contrario, son heterogéneos.

2.2. Monomios Semejantes
Si los monomios tienen la misma parte literal (Variables), se dice que son monomios semejantes. Por lo tanto, dos monomios semejantes solo se diferencian en los coeficientes.

Para afianzar el tema observa el siguiente video:
https://www.youtube.com/watch?v=iPZRUuyUp8o
Actividad2:
Realizar los ejercicios en el siguiente link sobre monomio. Al terminar envía el pantallazo con la calificación al docente por el WP.
https://www.superprof.es/apuntes/escolar/matematicas/algebra/polinomios/ejercicios-de-monomios.html
2.3. Factor común monomio
Un factor común monomio, es el factor que está presente en cada término del polinomio. En el caso de los coeficientes numéricos el factor común es el mayor divisor posible entre ellos
Ejemplo: Factorizar 8
Respuesta 8 = (4)(2)
y el factor común literal está conformado por el o los elementos de la parte literal (letra) presentes en todos los términos con el menor exponente.
Ejemplo:
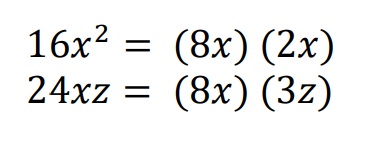
Factorizar un número es dar como respuesta dos factores, tales que al multiplicarlos nos den el número dado.

Pasos para factorizar expresiones algebraicas:
1. Hallar el Máximo Común Divisor de los Coeficientes.
2. Hallar la(s) variable(s) común con su menor exponente.
3. Dividir la expresión dada entre el factor común encontrado.
4. Agrupamos términos
No te olvides que al dividir los exponentes SE RESTAN
Ejemplo:
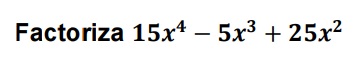
Paso 1: Halla el máximo común divisor 𝑀𝐶𝐷 (15, 5, 25) = 5
Paso 2: Halla el máximo común divisor de la parte literal
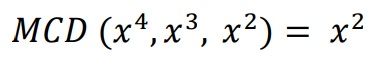
Paso 3: Escribir cada término utilizando el factor común obtenido
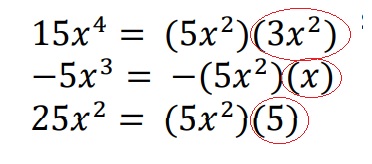
Paso 4: Agrupamos términos
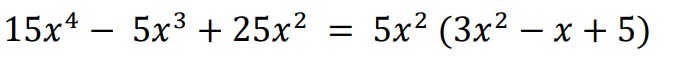
Y LISTO...
Otros ejemplos:
Ejemplo1:
Para factorizar por completo 10𝑥3 , podemos escribir la factorización en primos de 10 como 2𝑥5 y escribir 𝑥3 , como 𝑥 . 𝑥 . 𝑥. Por lo tanto, esta es la factorización completa de 10𝑥 a la 3

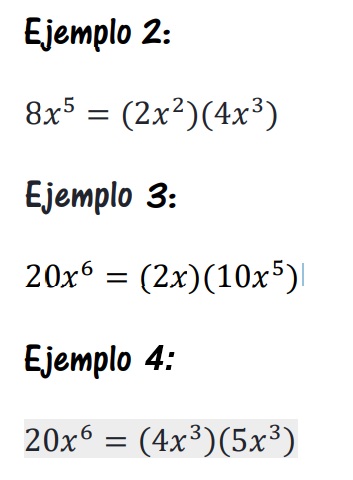
Actividad 3:
1. Factorizar utilizando los 4 pasos:
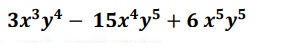
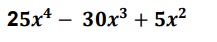
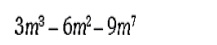
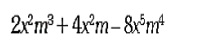
2. Relaciona con una flecha la expresión algebraica con su respectiva factorización
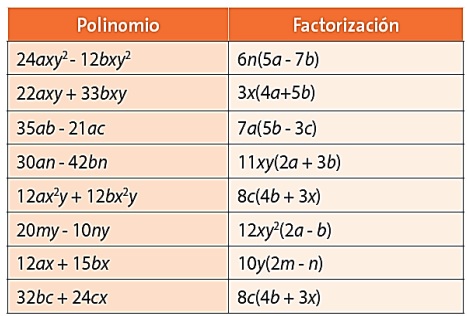
3. FACTORIZACIÓN DE BINOMIOS
Estándar:
En este tema se analizarán los procedimientos, que se pueden usar con un binomio para ser factorizado, tales como la diferencia de cuadrados, suma o diferencia de potencias iguales y suma o diferencia de cubos.
3.1. Diferencia de cuadrados
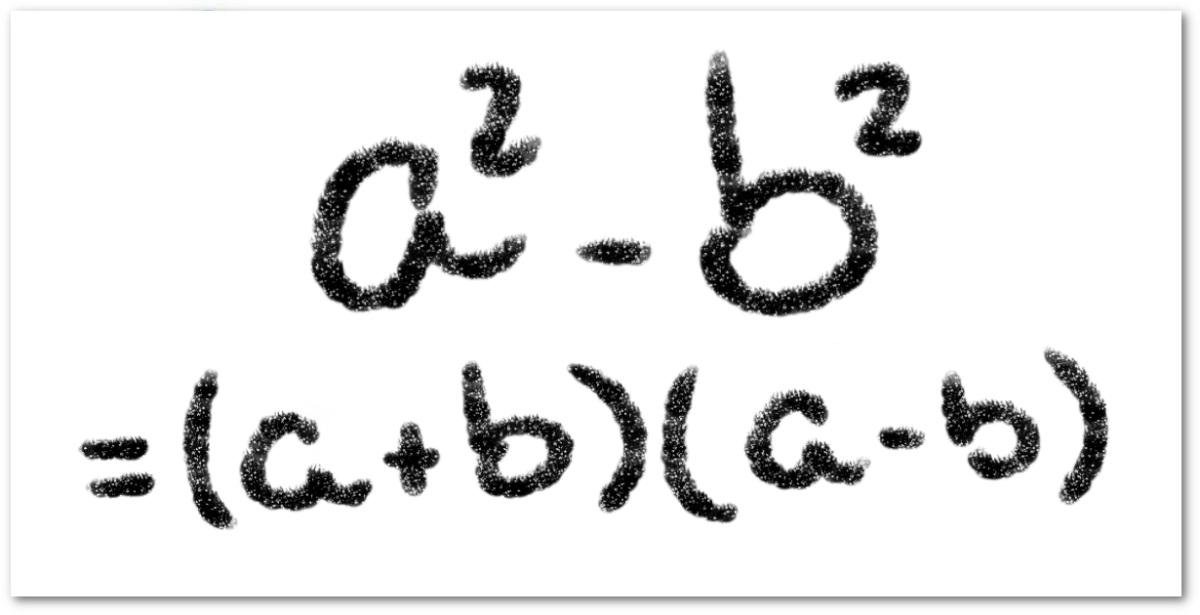
La diferencia de dos cuadrados es un teorema que nos dice si es que una ecuación cuadrática puede ser escrita como un producto de dos binomios, en donde uno muestra la diferencia de las raíces cuadradas y el otro muestra la suma de las raíces cuadradas.
Fórmula:
La fórmula de la diferencia de cuadrados es una forma algebraica que es usada para expresar la diferencia entre dos valores elevados al cuadrado. Una diferencia de cuadrados es expresada en la forma:






Ejemplo 5:
Factorizar:
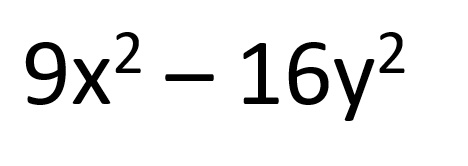
Se calcula la raíz cuadrada de cada uno de los términos, obteniendo:
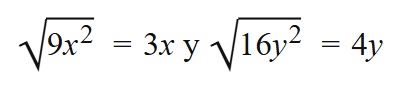
Luego la factorización será:
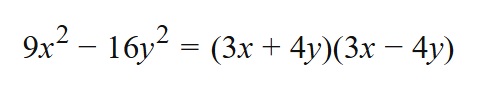

Para reforzar el tema te invito a observar los siguientes videos:
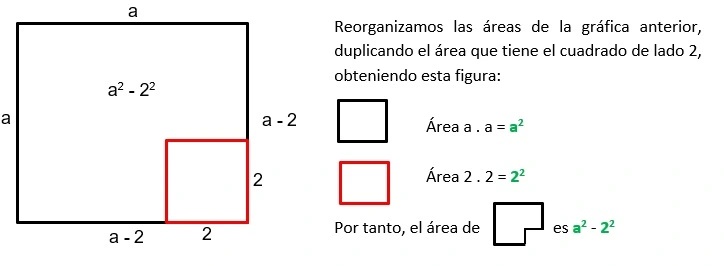
Representación gráfica:
Lo representaremos gráficamente para ver el proceso que se realiza desde el trabajo con áreas, es decir, representamos un cuadrado de lado a, en el cual dividimos un cuadrado de lado 2.
Taller 4:
1. Factoriza los siguientes ejercicios, con la ayuda de un compañero:
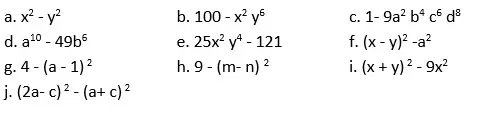
2. Realizar los siguientes ejercicios en el cuaderno utilizando el método de factorización de binomios para diferencia de cuadrados:
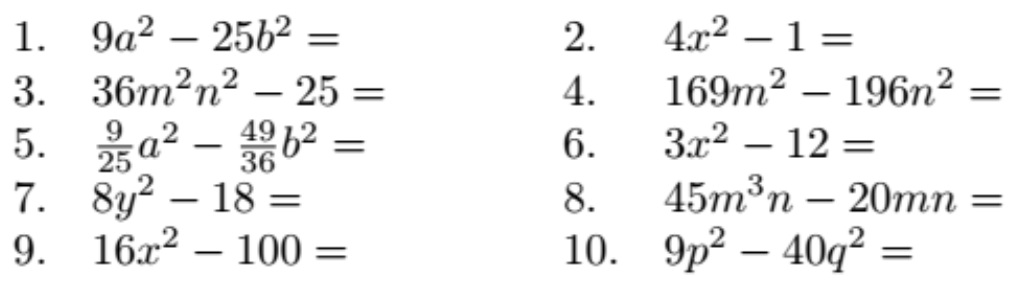
4. Escoje una de las cuatro respuestas
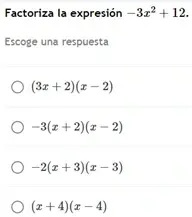
5. Ingresa al siguiente link y juega sobre el tema (No se te olvide enviar el pantallazo al wp del grupo):
https://www.cerebriti.com/juegos-de-matematicas/factorizacion-diferencia-de-cuadrados
3.2. Cubo perfecto de Binomio
También llamado Un binomio al cubo o cubo de un binomio (suma) es igual al cubo del primero, más el triple del cuadrado del primero por el segundo, más el triple del primero por el cuadrado del segundo, más el cubo del segundo. Para la resta semintercalan los signos comenzando por el menos.

EJEMPLO:
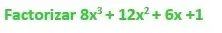
Paso1: Verificar si esta expresión cumple con las condiciones para ser considerada como cubo de un binomio:
a. Tiene cuatro términos
b. Dos términos (el primero y el último) son cubos perfectos, es decir existe su raíz cubica dentro del conjunto de los Enteros.
c. El segundo término es tres veces el producto de la primera raíz elevada al cuadrado por la segunda raíz elevada a la potencia uno.
d. El tercer término es tres veces el producto de la primera raíz elevada a la potencia de uno por la segunda raíz elevada al cuadrado.
DESARROLLO DEL EJERCICIO
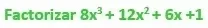

Paso2: Se hallan las raíces cubicas de los términos, primero y último, se verifica si los términos son positivos se establece una adición entre los mismos, en caso de presentarse los signos positivos y negativos de forma intercalada, entonces se establece una sustracción.







