Grado 8 - Matemáticas
Periodo 4 - Funciones
DBA 10. Proponer relaciones o modelos funcionales entre variables e identificar y analizar propiedades de covariación entre variables, en contextos numéricos, geométricos y cotidianos y las representa mediante gráficas (cartesianas, de puntos, continuas, formadas por segmentos, etc.) :
Estandar básico: Identifico y utilizo diferentes maneras de definir y medir la pendiente de una curva que representa en el plano cartesiano situaciones de variación
TEMAS: 1-Función lineal. 2-Función afín. 3-Pendiente de la recta. 4-Ecuación de la recta. 5-Rectas paralelas y perpendiculares
Conocimientos previos:
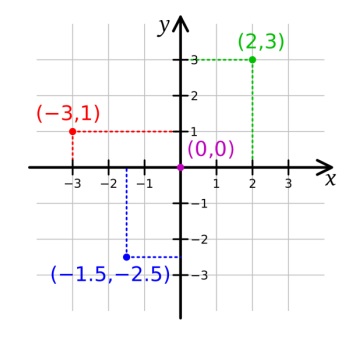
Plano cartesiano: En el plano cartesiano se ubica una pareja ordenada (a,b), primero se ubica a en el eje x y luego b en el eje y, se trazan líneas punteadas desde a hasta encontrar b, éste punto de encuentro es el que corresponde a la coordenada (a,b).
Ejemplo: Ubicar los puntos (2,3) - (-3,1) - (0,0) - (-1.5,-2.5)
Te invito a observar el siguiente video:
1. FUNCIÓN LINEAL
Una función lineal es una función polinómica de grado 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Son funciones rectas de la forma:
y = mx
Dónde
𝑦: 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑎 𝑙𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
𝑥: 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑎 𝑙𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑖𝑛𝑑𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
𝑚: 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑎 𝑙𝑎 𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡e
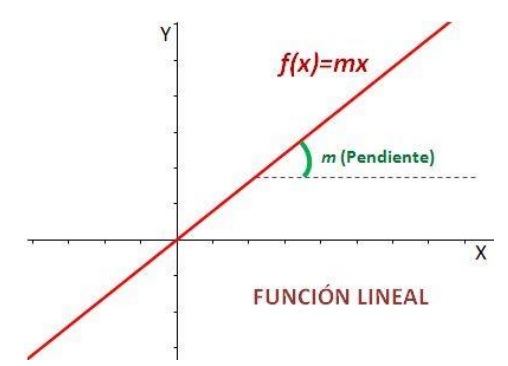
La pendiente es la inclinación con respecto al eje X (eje de abscisas). Si m es positiva (m > 0), entonces la función es creciente. En cambio, si la m es negativa (m < 0), entonces la función es decreciente.
La pendiente m significa que si aumentamos la x en una unidad, la y aumenta en m unidades. Si la m es positiva, según aumente la x la y también irá aumentando (función creciente).
En cambio, si m es negativa, cuando aumenta la x la y disminuirá (función decreciente).
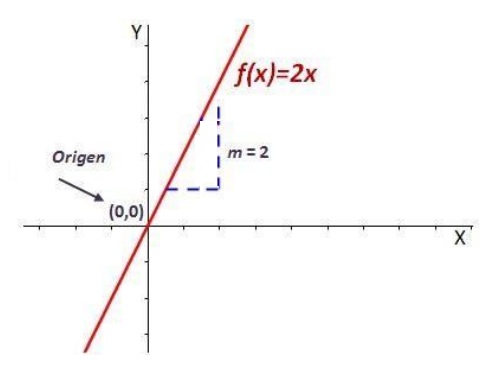
Por ejemplo: Sea una función 𝒇(𝒙) = 𝟐𝒙. El escalar m es 2 el coeficiente que multiplica al eje X (eje de abscisas). m es positiva (m > 0), la función es creciente.
2. FUNCIÓN AFÍN
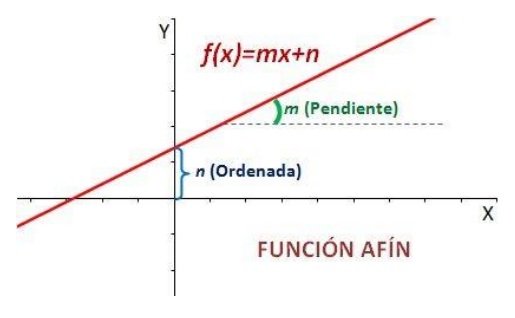
Una función afín es una función polinómica de primer grado que no pasa por el origen de coordenadas, o sea, por el punto (0,0). Las funciones afines son rectas definidas por la siguiente fórmula:
y = mx + b
Dónde
𝑦: 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑎 𝑙𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
𝑥: 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑎 𝑙𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑖𝑛𝑑𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
𝑚: 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑎 𝑙𝑎 𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡e
𝑏: 𝑟𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑎 𝑒𝑙 𝑝𝑢𝑛𝑡𝑜 𝑑𝑒 𝑐𝑜𝑟𝑡𝑒 𝑐𝑜𝑛 𝑒𝑙 𝑒𝑗𝑒 y
Ojo: Los valores de m y b son diferentes de 0.
La 𝒎 es la pendiente de la recta. La pendiente es la inclinación con respecto al eje de abscisas (eje X). Si m es positiva (𝑚 > 0), entonces la función es creciente. En cambio, si la m es negativa (𝑚 < 0), entonces la función es decreciente.
La pendiente 𝒎 significa que si aumentamos la x en una unidad, la y aumenta en 𝑚 unidades.
Si la m es positiva, conforme aumentemos la x la y también irá aumentando (función creciente).
En cambio, si m es negativa, conforme se aumenta la x la y disminuirá (función decreciente).
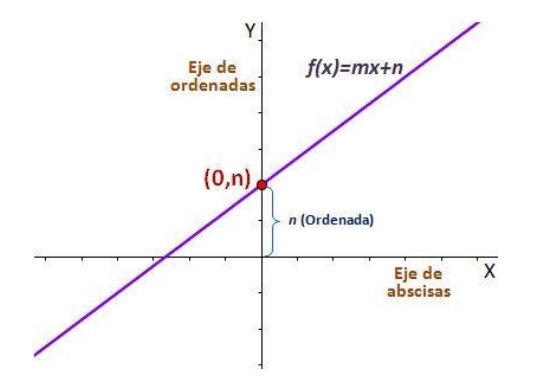
La ordenada (Y) en el origen es la b, es decir, el punto donde la recta corta el eje de ordenadas. Las coordenadas de este punto son (0,b)
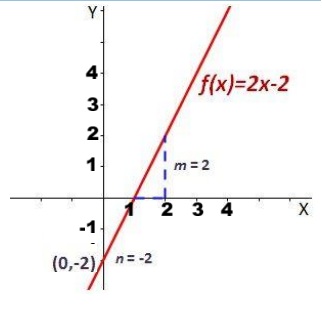
Por ejemplo: Sea una función 𝑓(𝑥) = 2𝑥 − 2. En este caso, m que es el coeficiente que multiplica a la x es
𝑚 = 2 y la ordenada es 𝑏 = −2. La función es afín porque tanto m como n son diferentes de 0 (𝑚 ≠ 0 𝑦 𝑏 ≠ 0).
CÓMO GRAFICAR UNA FUNCIÓN AFÍN
Para graficar una función afín es importante seguir los siguientes pasos.
Paso 1. Identificar en la función los valores de 𝑚 y 𝑏.
Paso 2. Establecer una tabla de valores para conocer los puntos que se ingresarán en la gráfica.
Paso 3. Tabular los valores de la tabla en la función.
Paso 4. Representar los puntos en el plano cartesiano.
Ejemplo:
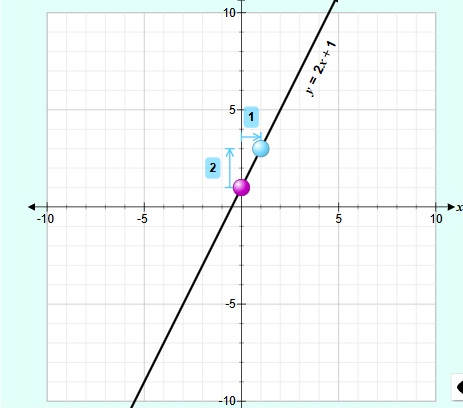
𝑦 = 2𝑥 + 1
Paso 1: Identificar valores de m y b. 𝑚 = 2 𝑦 𝑏 = 1
Paso 2: Tabla con valores

Paso 3: Tabulamos (reemplazamos) los valores de x en la función 𝑦 = 2𝑥 + 1

Paso 4: Colocamos los puntos en el plano cartesiano
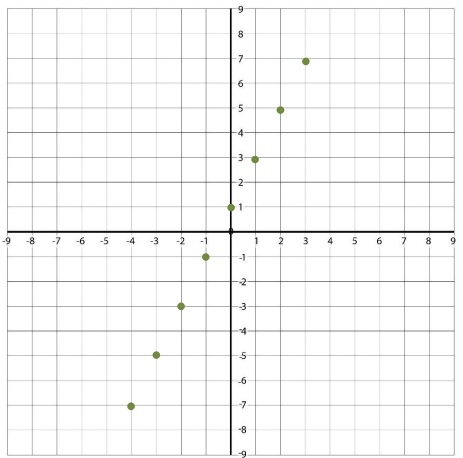
Paso 5: Unimos los puntos con una recta
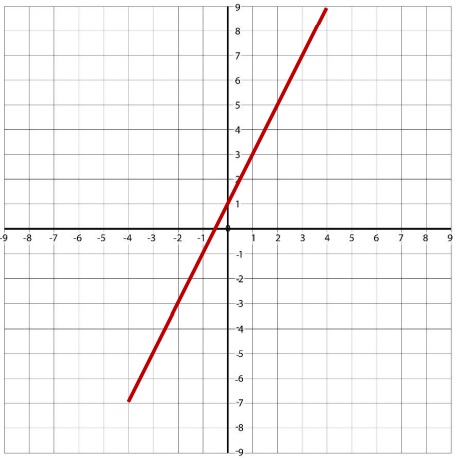
Si se te dificultó el tema te invito a observar el siguiente video:
ACTIVIDAD 1:
1. Entrar al siguiente enlace: https://phet.colorado.edu/sims/html/graphing-slope-intercept/latest/graphing-slope-intercept_all.html, es una actividad interactiva tipo juego, deberás dibujar el ejercicio anterior 𝑦 = 2𝑥 + 1.
2. Construir una tabla de valores −4 < 𝑥 < 4 para cada una de las siguientes funciones, realizar su gráfica y dibujarlo con la aplicación del punto 1 y comparalo con tu resultado:
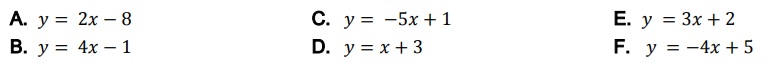
3. PENDIENTE DE UNA RECTA
Antes de entrar en el tema veremos el concepto de linea recta y distancia:
En geometría euclidiana, la recta o la línea recta es una línea que se extiende en una misma dirección; por lo tanto, tiene una sola dimensión y contiene un número infinito de puntos. Dicha recta también se puede describir como una sucesión continua de puntos extendidos en una sola dirección.
Distancia entre dos puntos. Dados dos puntos cualesquiera A(x1,y1), B(x2,y2), definimos la distancia entre ellos, d(A,B), como la longitud del segmento que los separa.
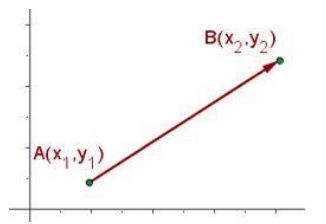
Para hallar la pendiente entre dos puntos utilizamos la siguiente fórmula:
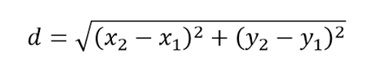
EJEMPLO : Hallar la distancia entre los puntos A(-3,5) y B(-7,1). A estaría definido por (x1,y1), B (x2,y2)
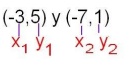
Reemplazamos los valores:
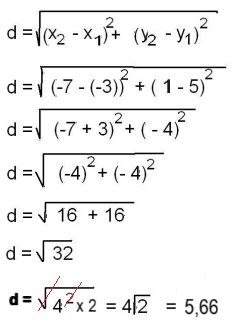
La gráfica quedaría de la siguiente forma:
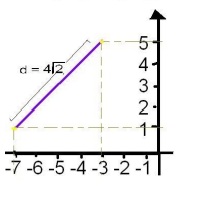
Como ya vimos en el tema de función lineal y función afín la pendiente de la recta es la distancia que se forma con la línea hacia el eje X. En la gráfica la podemos observar que la pendiente es -4, ya que decrece y la hallamos restando x2 - x1, en este caso (-7 -(-3)) es decir (-7+3) = -4, es decir su pendiente decrece.
Muchas veces no tenemos la gráfica para observar, en este caso hallaremos la pendiente con la fórmula que veremos en el siguiente tema:
Pendiente de una recta. Dados P1 (x1; y1) y P2 (x2; y2), como dos puntos de una recta no paralela al eje Y; su pendiente m está dada por la fórmula:
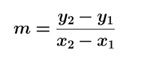
Ejemplo: Tenemos los siguientes puntos A(-3,5) y B(-7,1), Recuerda que el punto A estaría definido por (x1, y1) y el punto B por (x2, y2). Hallar la pendiente utilizando la fórmula antes vista
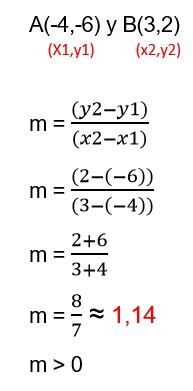
Sino te quedó claro el tema, te invito a observar el siguiente video:
ACTIVIDAD 2:
Responde en el cuaderno:
1. Los puntos (1, 1) y (3, 5) son parte de una recta. ¿Cuál es la pendiente de la recta?
2. ¿Cuál es la pendiente de una recta que tiene los puntos (2, 1) y (4, 5)?
3. Una recta contiene a los puntos (2, 3) y (6, 5). ¿Cuál es su pendiente?
4. Tenemos los puntos (3, 2) y (6, 3) que son parte de una recta. ¿Cuál es la pendiente?
5. Determina la pendiente de una recta que contienen a los puntos (-1, 3) y (6, -4).