GEOMETRÍA
Grado 7 - Periodo 1
Geometría de Líneas y Ángulos
Triángulos y Congruencia

LOGROS.
- Identifica relaciones de congruencia y semejanza entre las formas geométricas que configuran el diseño de un objeto (cuadriláteros, paralelogramos, trapecios, entre otros).
- Representa en el plano cartesiano la variación de magnitudes (áreas y perímetro) y con base en la variación explica el comportamiento de situaciones y fenómenos de la vida diaria.
ESTÁNDAR BÁSICO.
- Identifico características de localización de objetos en sistemas de representación cartesiana y geográfica.
- Identifico y describo fi guras y cuerpos generados por cortes rectos y transversales de objetos tridimensionales.
Conocimientos previos:

Recordemos: Para considerar los ángulos generados entre dos paralelas cortados por una secante, es necesario recordar el significado de rectas paralelas y recta secante.
Al trazar dos rectas en un mismo plano, estas rectas pueden ser:

Tipos de rectas: (Visto en grado 6, primer periodo) te invitamos a recordar el tema con el siguiente video:
1. RELACIÓN ENTRE ÁNGULOS FORMADOS POR DOS RECTAS Y UNA TRANSVERSAL
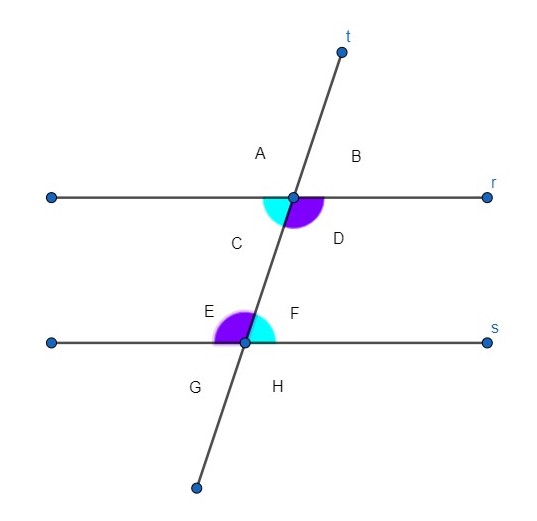
Las rectas r y s son paralelas y la recta t es secante.
Dos rectas paralelas cortadas por una recta secante forman ocho ángulos, los cuales en la imagen están señalados por letras minúsculas: a, b, c, d, e, f, g, h
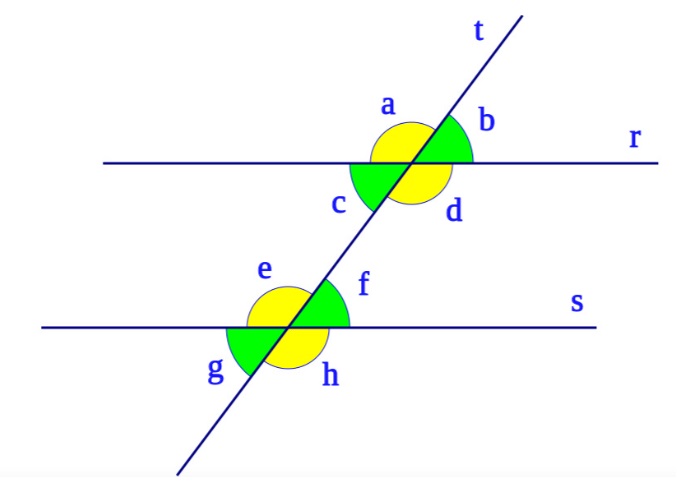
Estos, forman diferentes clases de ángulos, que se clasifican de acuerdo a las características que cumplan, de acuerdo a la posición que ocupen respecto a las rectas paralelas y a la recta secante. Estas son:
- Colaterales: Son los que se encuentran a un mismo lado de la secante, ambos externos o ambos internos
Externos: (a,g)(b,h)
Internos: (c,e)(d,f)
- Alternos internos: son los que se encuentran a distinto lado de la secante.
- Ángulos externos: son los que se encuentran al mismo lado de la secante.
(a,b,g,h)
- Alternos internos: son los que se encuentran en la zona interior de las rectas paralelas.
(c,f)(e,d)
- Alternos externos: Son los que se encuentran en la zona externa de las rectas paralelas.
(a,h)(b,g)
- Correspondientes: Son los que se encuentran a un mismo lado de la secante, uno es externo y el otro interno.
(a,e)(b,f)(c,g)(d,h)
- Opuestos por el vértice: son aquellos que se forman cuando dos líneas rectas se cruzan. Estos ángulos comparten el mismo vértice
(a,d)(c,b)(e,h)(f,g)
Observa el siguiente gráfico resumido por colores:
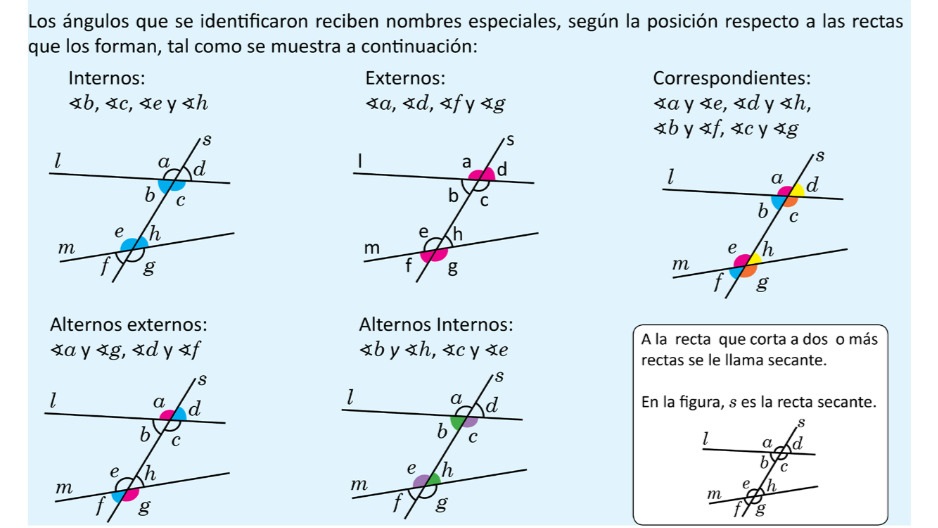
Te invito a observar el siguiente video sobre el tema:
Actividad 1:
Lo puedes desarrollar directamente en el siguiente link: https://rea.ceibal.edu.uy/elp/paralelas-y-transversales/ejercicios_i.html
1. Observa en la imagen los ángulos formados por dos rectas paralelas y una transversal a ellas:
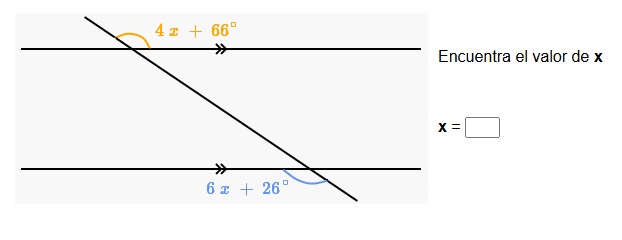
2. Observa en la imagen los ángulos formados por dos rectas paralelas y una transversal a ellas:
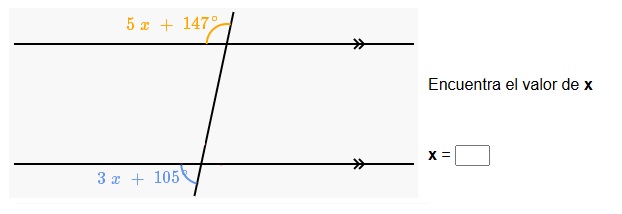
3. Observa en la imagen los ángulos formados por dos rectas paralelas y una transversal a ellas:
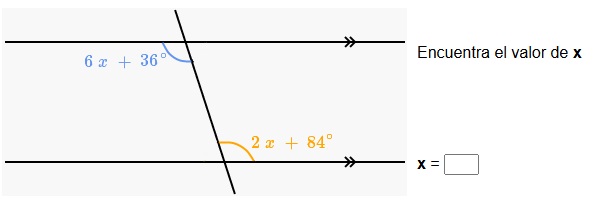
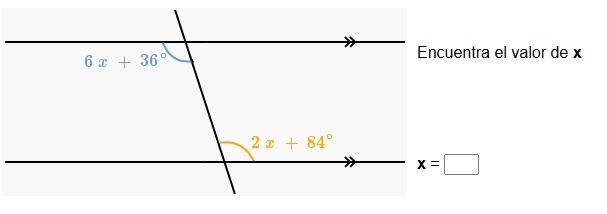
4. Observa en la imagen los ángulos formados por dos rectas paralelas y una transversal a ellas:
2. PROPIEDADES DE 2 LÍNEAS PARALELAS Y TANGENTES
Propiedades:
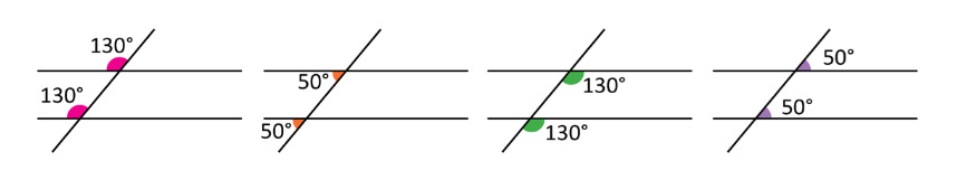
1. Si dos rectas paralelas son cortadas por una recta secante, los ángulos correspondientes son iguales, esta afirmación también se cumple con los ángulos alternos internos y alternos externos.
ÁNGULOS CORRESPONDIENTES
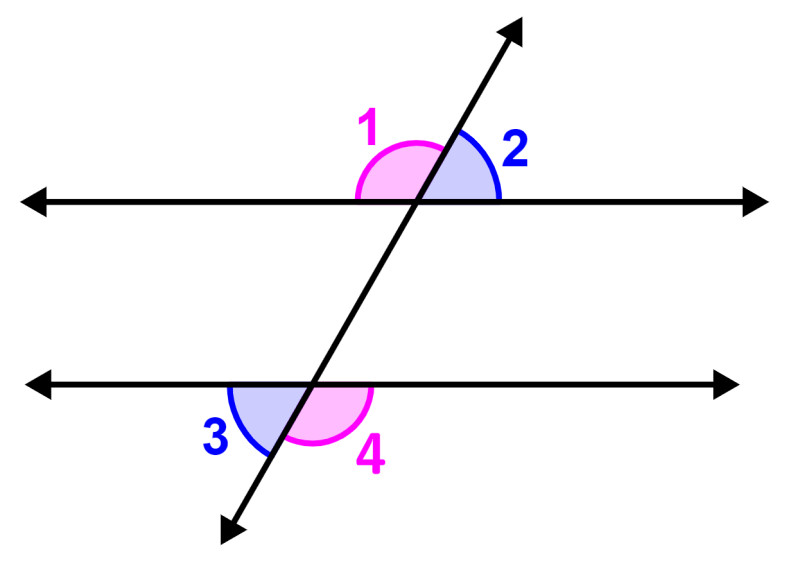
ÁNGULOS ALTERNOS INTERNOS
ÁNGULOS ALTERNOS EXTERNOS
2. Propiedad de serruchito: Ángulos que se abren a la derecha y ángulos que se abren a la izquierda, las sumas de los ángulos de la derecha son iguales a los de la izquierda
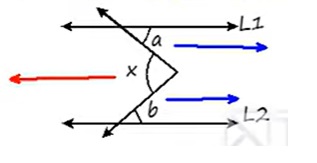
En este caso x = a + b
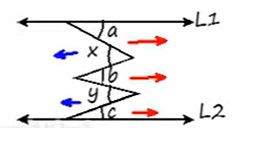
x + y = a + b + c
3. Propiedad de los segmentos: La suma de los ángulos alrededor de secantes (Como si fuera un triángulo) siempre es igual a 360°
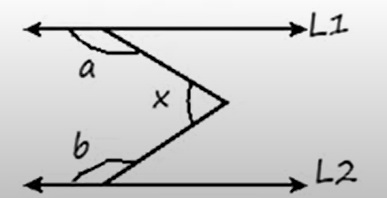
x + a + b = 360°
4. Propiedad de la ramita: La suma de todos los ángulos en la ramita entre dos paralelas es igual a 180°
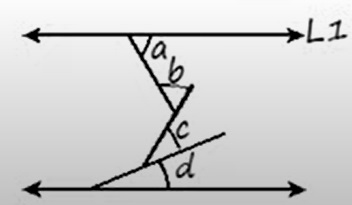
a + b + c + d = 180°
Ejemplo 1:
Si L1 || L2, halle (2θ + 5°)
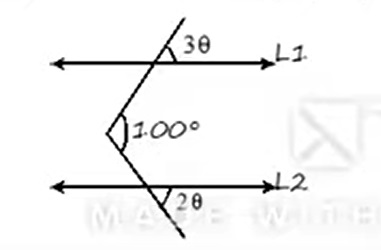
Acá aplicamos dos propiedades, primero la de ángulos opuestos por el vértice son iguales, es decir para 2θ y 3θ
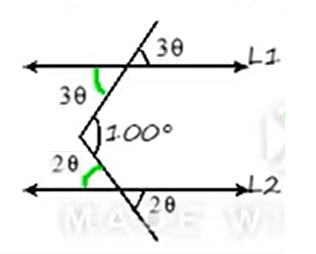
Luego, la propiedad del serruchito
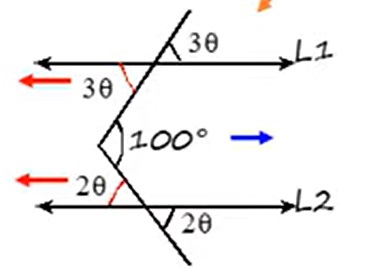
3θ + 2θ = 100°
5θ = 100°
θ = 100°/5
θ = 20°
Como me piden hallar 2θ + 5, reemplazo -----> 2 (20°) + 5° = 45°
Ejemplo 2:
SI L1 // L2, halle 3α
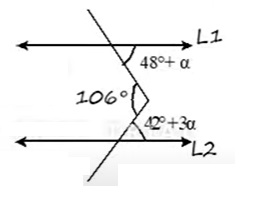
Para este ejercicio iniciamos con la ley del serruchito:
48° + α + 42° + 3α = 106°
4α + 90 = 106°
4α = 106° - 90°
4α = 16°
α = 16° / 4
α = 4°
Por tanto, 3α = 3 (4°) -----> 12°
Actividad 2:
1. Desarrolla la actividad de la siguiente página y enseñale el resultado a tu docente:
https://play.tomi.digital/es/app/learn?id=260853&type=lesson
A.

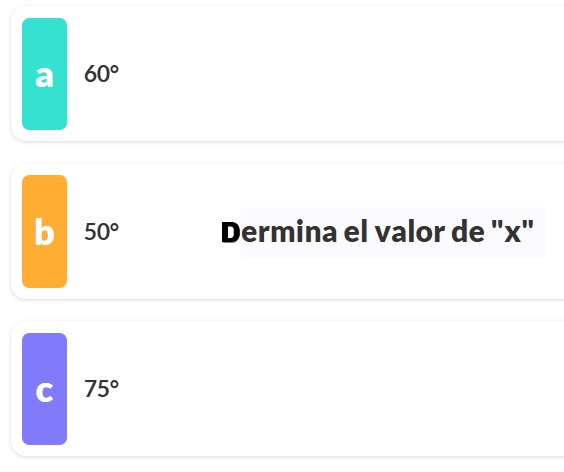
B.

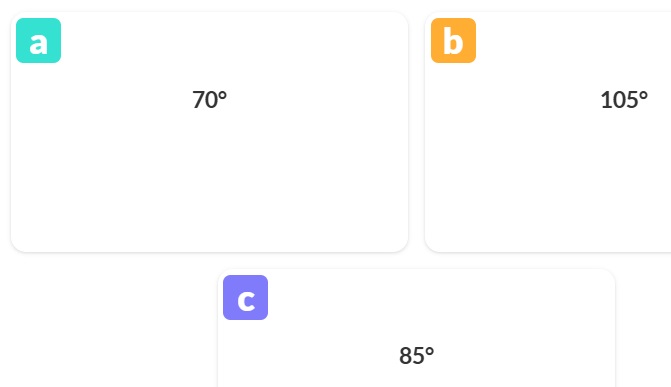
C.

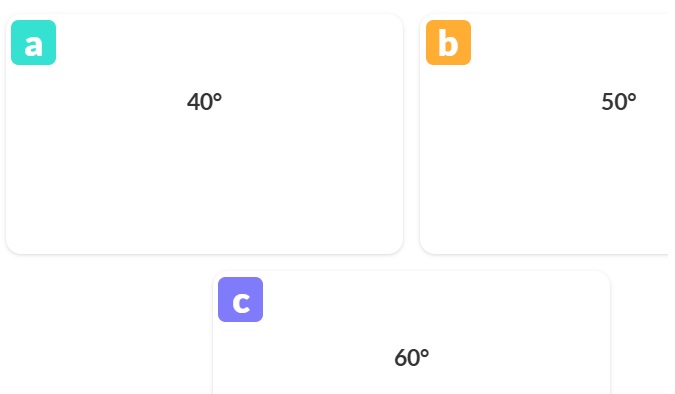
D.

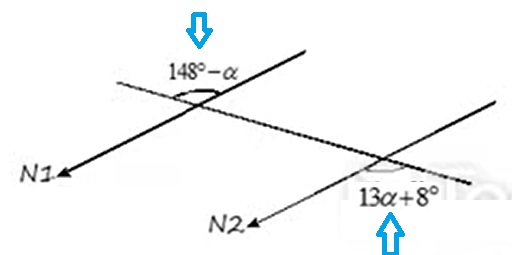
2. Si N1 // N2, halle (5α - 7°)
Nota: Se soluciona con la propiedad de alternos externos
3. PROPIEDADES DE LAS LINEAS PARALELAS Y PERPENDICULARES
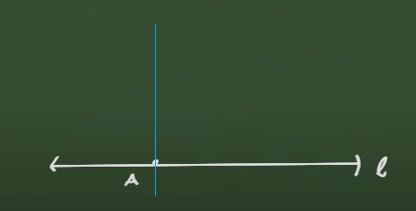
3.1. Perpendicularidad:
1. Por un punto exterior a una recta se puede trazar una y solamente una perpendicular a la recta dada

2. Por un punto perteneciente a una recta puede pasar una y solamente una perpendicular
3.2. Paralelismo:
3. Reflexividad: cualquier recta L, es paralela a ella misma o no se corta en ningún punto:

4. Simetría: Si L es paralela a M, L // M, entonces M // L, L=M
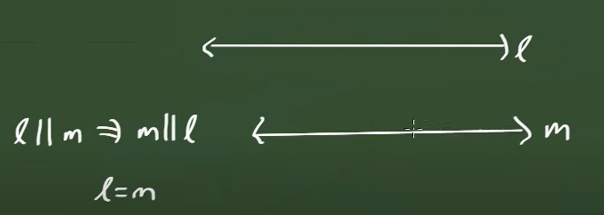
5. Transitividad: Si L es paralela a M y M es paralela a Q, entonces, L es paralela a Q
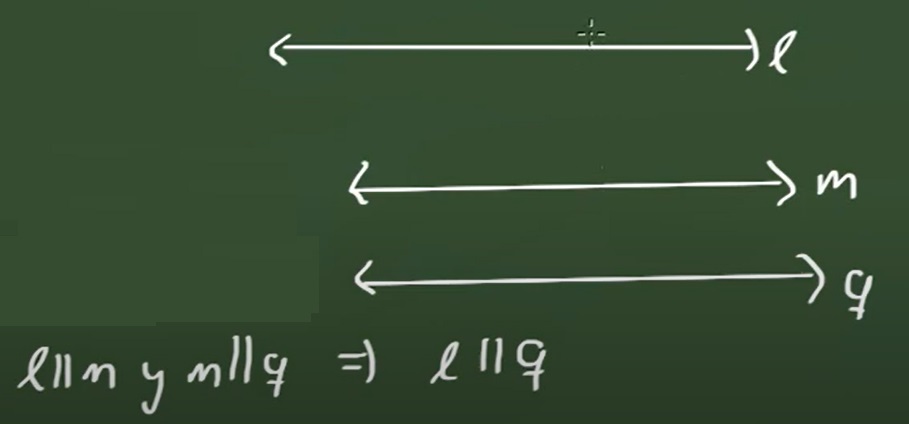
6. Postulado de las paralelas o quinto postulado de Euclides:
Por un punto exterior a una recta pasa una y solo una paralela a la recta dada.

TRIÁNGULOS Y CONGRUENCIA
Criterios de congruencia (LAL, LLL, ALA)
1. TRIÁNGULOS CONGRUENTES
Dos triángulos son congruentes si hay una correspondencia entre sus vértices de manera que cada par de lados y ángulos correspondientes sean congruentes. Obsérvese que la congruencia puede definir de manera similar para otras figuras.
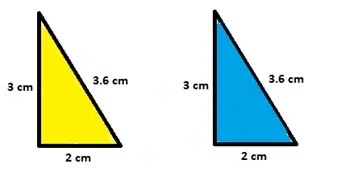
Definición:
Congruencia: Que tiene la misma medida.
Símbolo: (Ξ) Ej: AB≡CD
2. TEOREMAS Y POSTULADOS DE CONGRUENCIA
2.1. TEOREMAS
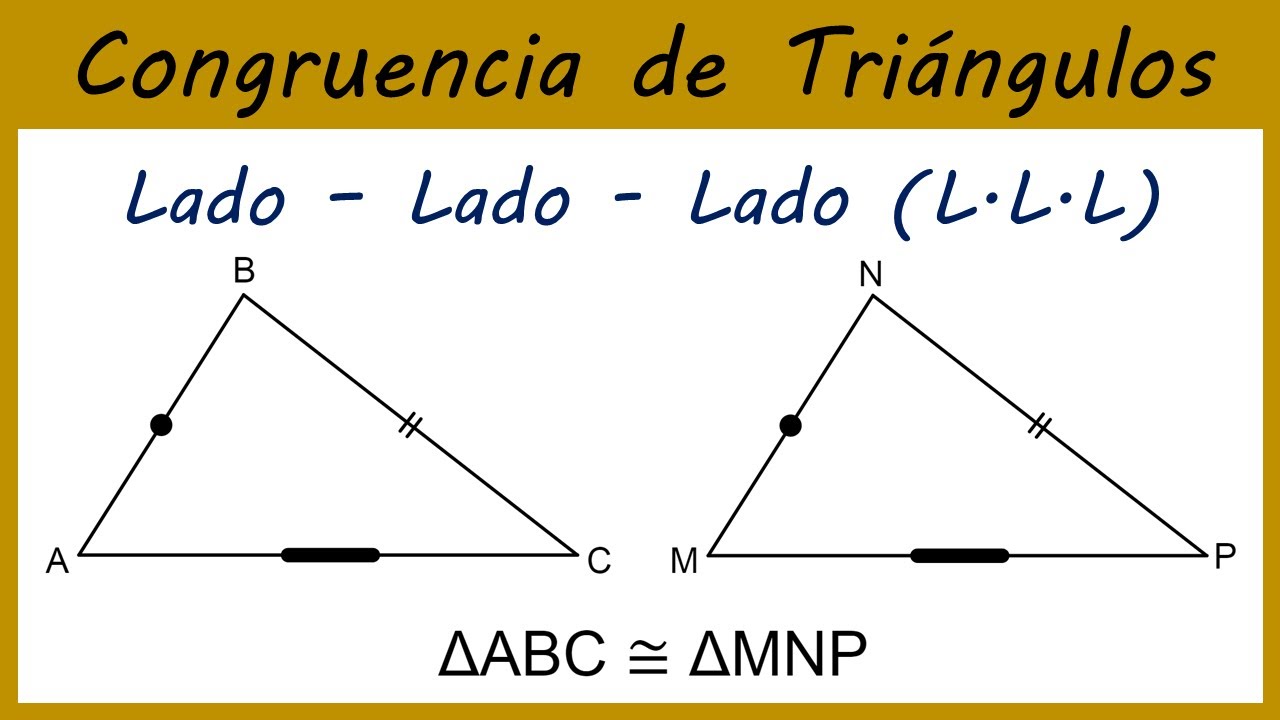
2.1.1. Teorema de congruencia LLL (lado - lado - lado)
Si tres lados de un triángulo son congruentes con tres lados de un segundo triangulo, entonces los dos triángulos son congruentes.
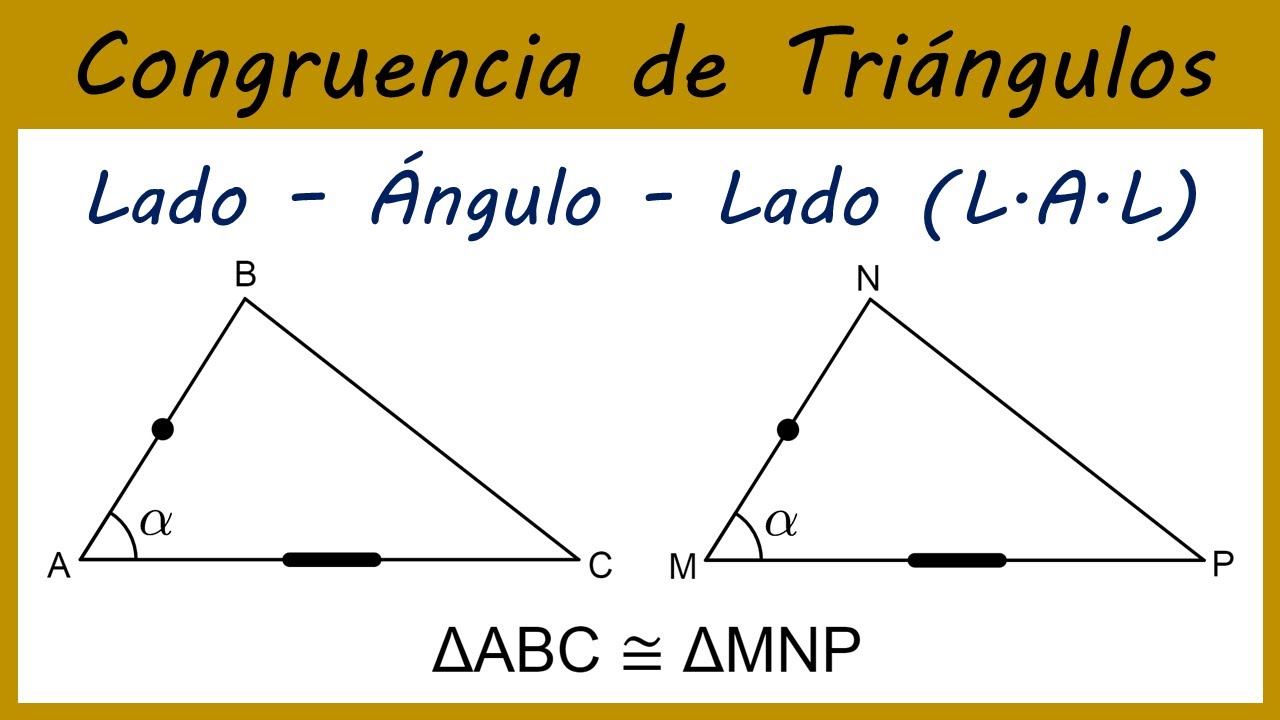
6.2.2. Teorema de congruencia LAL (lado - ángulo - lado)
Si dos lados y el ángulo incluido de un triángulo son congruentes a dos lados y el ángulo incluido de un segundo triangulo, entonces los dos triángulos son congruentes
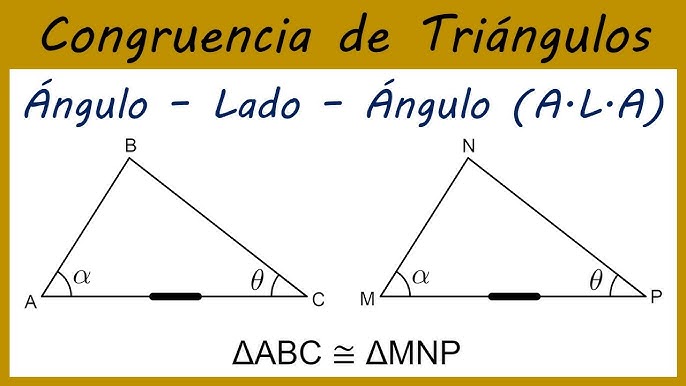
6.2.3. Teorema de congruencia ALA (ángulo - lado - ángulo)
Si dos ángulos y el lado incluido de un triángulo son congruentes con dos ángulos y el lado incluido de un segundo triangulo, entonces los dos triángulos son congruentes.
Actividad 3:
Pregunta 1: Para desarrollarlo ten en cuenta el tema visto de Ángulos alternos internos son iguales
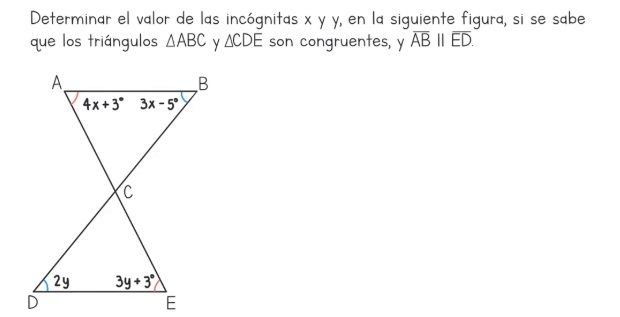
a. Son del mismo color.
b. Las medidas de sus lados correspondientes están dadas en centímetros.
c. Sus lados correspondientes son proporcionales dos a dos
2. Los triángulos de la imagen...
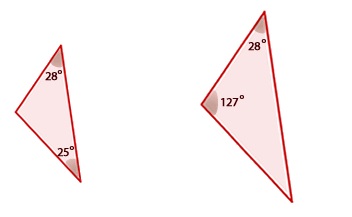
a. Se parecen, pero no son semejantes.
b. Son semejantes pues las medidas de sus ángulos homólogos son iguales.
c. No podemos afirmar nada, pues en ningún triángulo se dan las medidas de sus tres ángulos.
Propiedades de congruencia de triángulos isósceles y equiláteros
1. TRIÁNGULOS ISOCELES
La congruencia de figuras, es utilizada en la construcción arquitectónica, ensamble de equipo y mobiliario, diseño de interiores, fabricación de automóviles, reconstrucción de infraestructura, etc.

Teorema de ángulos base
Un triángulo isósceles está definido como un triángulo que tiene al menos dos lados congruentes. En esta lección probaras que un triángulo Isósceles también tiene dos ángulos congruentes opuestos a los dos lados congruentes. Los lados congruentes del triángulo isósceles son llamados los catetos del triángulo. Sl otro lado es llamado base y los ángulos entre la base y los lados congruentes son llamados ángulos base. El ángulo formado por los dos catetos del triángulo isósceles se llama ángulo vértice.
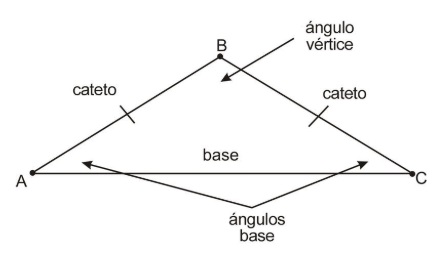
El Teorema de ángulos base establece que, si dos lados de un triángulo son congruentes, entonces sus ángulos opuestos también son congruentes. En otras palabras, los ángulos base de un triángulo isósceles son congruentes.
Nota: este teorema no nos dice sobre el ángulo vértice.
Ejemplo 1
¿Cuáles son los dos ángulos que deben ser congruentes en el diagrama de abajo?
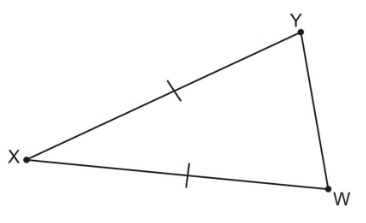
Solución:
El triángulo en el diagrama es un triángulo isósceles. Para encontrar los ángulos congruentes, tú necesitas encontrar los ángulos que son opuestos a los lados congruentes.
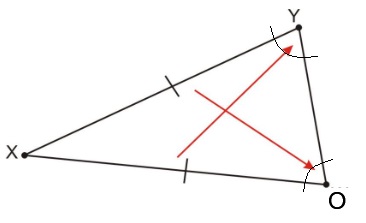
Este diagrama muestra los ángulos congruentes. Los ángulos congruentes en el triángulo son
∠ XYO y ∠ XOY.
Entonces, ¿cómo probamos el teorema de ángulos base? Usando triángulos congruentes.
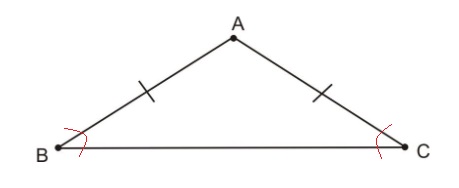
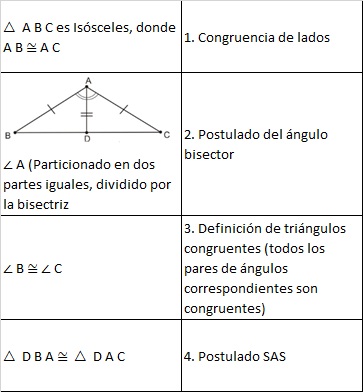
Dado: △ Isósceles A B C donde los lados A B ≅ A C
Probar que ∠ B ≅ ∠ C
TRIÁNGULOS EQUILATEROS
El teorema de los ángulos bases también se aplica a triángulos equiláteros. Por definición, todos los lados en un triángulo equilátero tienen exactamente la misma longitud.
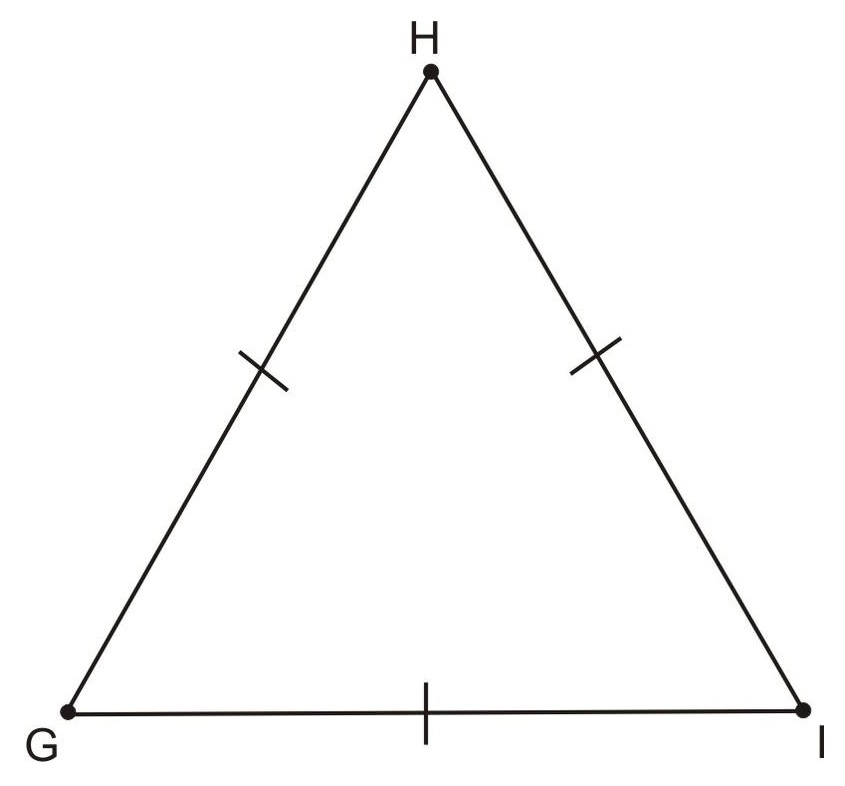
Por el teorema de ángulos base, conocemos que ángulos opuestos a lados congruentes en un triángulo isósceles son congruentes. Entonces, si los tres lados del triángulo son congruentes, entonces todos los ángulos son congruentes también.
Un triángulo que tiene todos los ángulos congruentes se llama un triángulo equiangular. Así, como resultado del teorema de ángulos base, tú puedes identificar que todos los triángulos equiláteros son también triángulos equiangulares.
Inverso del teorema de ángulos base
Como sabes, algunos teoremas tienen un inverso que también es verdadero. Recuerda que un inverso revierte el enunciado de un teorema. Por ejemplo, Si digo, "Si abro un grifo, entonces sale agua", He hecho un enunciado. El inverso de ese enunciado es: "Si no hay agua saliendo del grifo, entonces no he abierto el grifo". En este caso, el inverso no es verdadero. Por ejemplo, el grifo puede tener una fuga. Así que, como puedes ver, los enunciados inversos son algunas veces verdaderos, pero no siempre.
El inverso del teorema de ángulos bases es siempre verdadero. El teorema de ángulos bases establece que si dos lados de un triángulo son congruentes los ángulos opuestos a ellos también son congruentes. El inverso de este enunciado es que, si dos ángulos en un triángulo son congruentes, entonces los lados opuestos a ellos también serán congruentes. Puedes usar esta información para identificar triángulos isósceles en muchas y diferentes circunstancias.
Ejemplo 2
¿Cuáles de los dos lados deben ser congruentes en el diagrama de abajo?
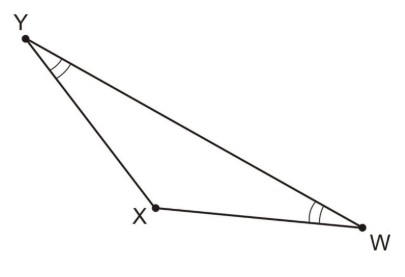
△ YXW tiene dos ángulos congruentes. Por el inverso del teorema de ángulos base, es un triángulo isósceles.
Para encontrar los lados congruentes, necesitas encontrar los lados que son opuestos a los ángulos congruentes.
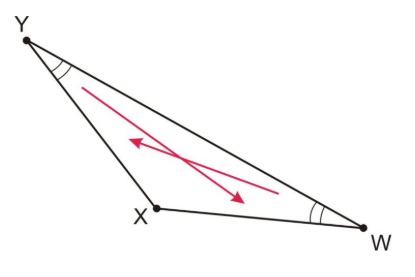
Este diagrama muestra flechas señalando a los lados congruentes. Los lados congruentes en este triángulo son XY y XW.
La prueba del inverso del teorema de los ángulos base dependerá de unas cuantas propiedades más de los triángulos isósceles que probaremos después, así que por ahora omitiremos esa prueba.
Actividad 4:
- Dibujar y etiquetar el △ A B C isósceles, con catetos A B y B C que tiene un ángulo vértice que mide 118°.
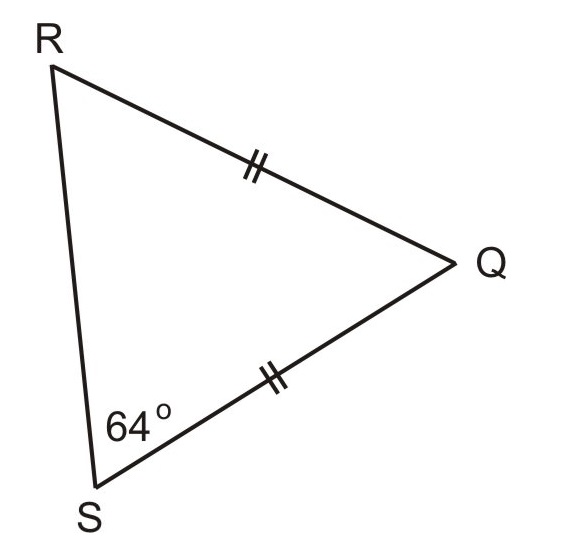
- ¿Cuál es la medida de cada ángulo base en el triángulo △ R S Q?
3. ¿Cuál de los siguientes enunciados debe ser verdadero sobre los ángulos base de un triángulo isósceles?
A. Los ángulos bases son congruentes.
B. Los ángulos base son complementarios.
C. Los ángulos base son agudos.
D. Los ángulos base pueden ser ángulos rectos.
Ángulos interiores y exteriores de triángulos
¿Qué son los ángulos interiores?
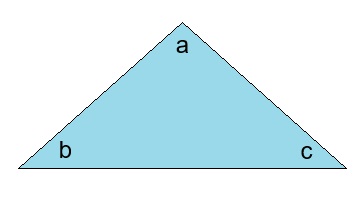
Un polígono es una figura bidimensional cerrada formada por varios segmentos rectos (llamados lados). En un polígono, un ángulo interior es un ángulo que se encuentra dentro del polígono. Un triángulo tiene tres lados y tres ángulos interiores. En el triángulo de abajo, los tres ángulos interiores se denominan a, b y c.
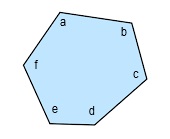
Otros polígonos tienen más de tres ángulos interiores. El número de ángulos interiores de un polígono siempre es igual a su número de lados. Por ejemplo, un hexágono como el de abajo tiene seis lados y seis ángulos interiores.
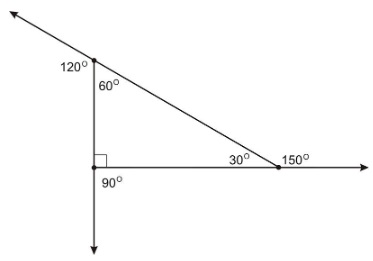
¿Qué son los ángulos exteriores?
Para formar un ángulo externo, se extiende uno de los lados más allá del ángulo. El ángulo formado por el lado extendido y el lado adyacente al original se llama ángulo externo . Este ángulo siempre será menor que 180°.
Propiedades de los ángulos de un triángulo:
1. La suma de los ángulos internos de cualquier triángulo es 180º
2. La suma de las medidas de los ángulos externos de un triángulo es 360º.

3. La medida de un ángulo exterior es igual a la suma de las medidas de los ángulos interiores no adyacentes a dicho ángulo.
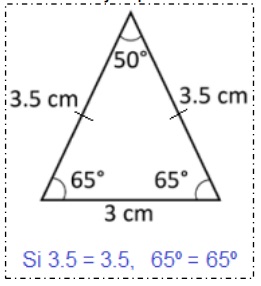
4. Si dos lados de un triángulo son congruentes, entonces los ángulos opuestos a esos lados son congruentes (aplica para triángulos isósceles).
Propiedades de los lados de un triángulo:
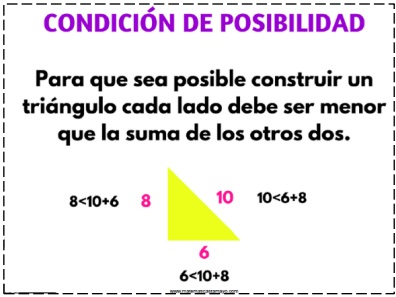
1. En un triángulo, la medida de uno de los lados es menor que la suma de los otros dos y mayor que la diferencia. (Condición de unicidad).
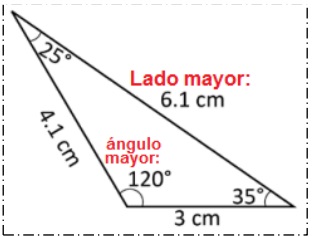
2. En un triángulo, al lado mayor se opone el ángulo mayor.
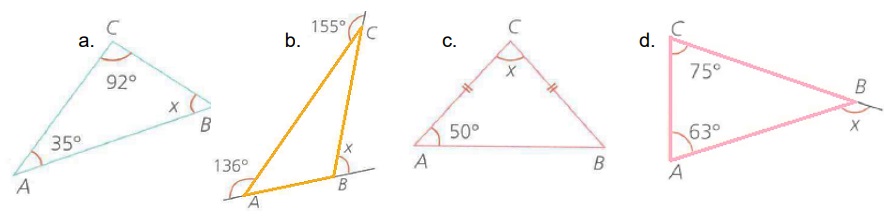
Actividad 5: (Responde en el cuaderno)
1. Determine el valor del ángulo x en cada caso.
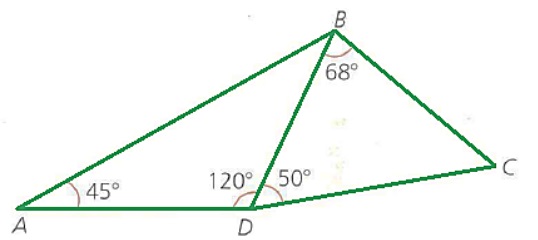
2. Determina cuál es el lado más corto en cada uno de los triángulos de la siguiente figura. Explica tu respuesta:
3. Escribe si cada afirmación es verdadera o falsa según corresponda:
a. En el triángulo formado por los segmentos 𝑎 = 3 𝑐𝑚, 𝑏 = 4 𝑐𝑚 y 𝑐 = 5 𝑐𝑚, el ángulo con mayor abertura es el opuesto al lado b. V ( ) F ( )
b. ¿Es posible construir un triángulo cuyos lados midan 8 𝑐𝑚, 3 𝑐𝑚 y 7 𝑐𝑚? V ( ) F ( )
c. En un triángulo, ¿los ángulos interiores pueden medir 45º, 32º y 50º? V ( ) F ( )
d. ¿Es posible construir un triángulo cuyos lados midan 5 𝑐𝑚, 11 𝑐𝑚 y 6 𝑐𝑚? V ( ) F ( )
e. Los ángulos exteriores de un triángulo miden 120º, 100º y 110º respectivamente? V ( ) F ( )
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
ACÁ PUEDES DESCARGAR LA GUÍA:
ACUERDOS PEDAGÓGICOS:
RÚBRICA:
Ángulos y ángulos entre rectas paralelas
Congruencia de triángulos