Grado 6 - Periodo 4
Matemáticas

Tema: Números enteros
1. Concepto de número entero 2. Representación de números enteros en la recta 3. Números opuestos 4. Valor absoluto 5. Operaciones con números enteros (adición, sustracción, multiplicación, división).
DBA2. Utiliza las propiedades de los números enteros y racionales y las propiedades de sus operaciones para proponer estrategias y procedimientos de cálculo en la solución de problemas
Conocimientos previos: números naturales
1. CONCEPTOS BÁSICOS DE LOS NÚMEROS ENTEROS
Antes de comenzar el tema te invito a observar el siguiente video:
1.1. Concepto.
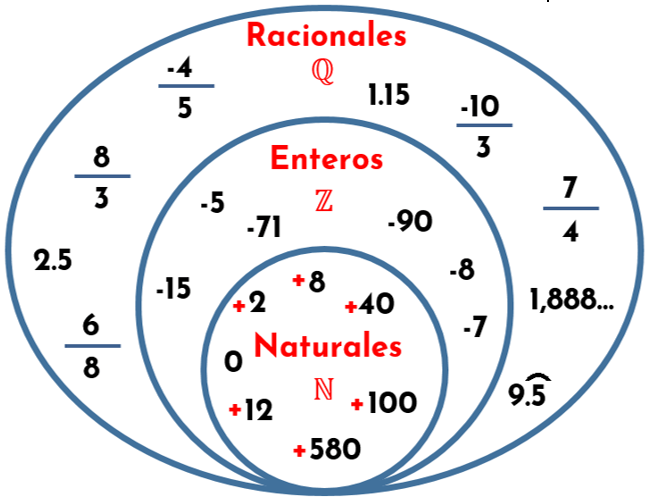
Ahora si aterricemos lo visto en el video: Los números enteros son el conjunto numérico que abarca la totalidad de los números naturales, sus inversos negativos y el cero. Es decir, se trata de los números que se utilizan para contar, junto con sus opuestos de signo negativo (1 y -1). Normalmente, los enteros negativos se escriben con su signo (-), cosa que no hace falta para los positivos, pero puede hacerse en ocasiones para resaltar la diferencia (+1 y -1).
El conjunto de números enteros se corresponde con la letra Z, proveniente del vocablo alemán zahl ("número" o "cantidad"). Se lo suele representar como una recta numérica, con el cero ubicado en el medio y, a partir de él, los números positivos (Z+) desplegados hacia la derecha y los números negativos (Z-) desplegados hacia la izquierda, en ambos casos extendiéndose hasta el infinito.
De esta manera, los enteros positivos crecen hacia la derecha, mientras que los negativos lo hacen hacia la izquierda. Esto significa que las cantidades son más grandes hacia el infinito positivo (+∞) y más pequeñas hacia el infinito negativo (-∞)
La aparición de los números enteros permitió agrandar la cantidad de operaciones posibles con los números naturales, ya que las cifras negativas permiten realizar operaciones más complejas, como restarle a un número otro mayor (5 – 7 = -2).
Esto es sumamente útil para el cálculo y registro de ganancias y pérdidas, de deudas, e incluso de ciertas magnitudes como la temperatura, en el que se emplean valores sobre cero (positivos) y bajo cero (negativos).

2. Representación de los números enteros en la recta numérica
Como decíamos antes, los números negativos se consideran como los opuestos de sus simétricos positivos y viceversa. Es así que:
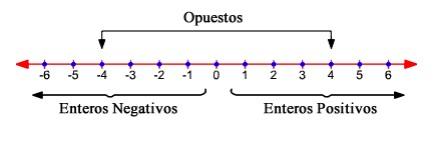
ORDEN DE LOS NÚMEROS ENTEROS
Para ordenar los números enteros se pueden considerar las siguientes observaciones:
1.- Todo número entero a la derecha del cero en la recta numérica, es positivo.
2.- Todo número entero a la izquierda del cero en la recta numérica, es negativo.
3.- Todo número entero que esté a la derecha de otro en la recta numérica, es mayor que él.
4.- Todo número entero que esté a la izquierda de otro en la recta numérica, es menor que él.
5.- Todo número negativo es menor que cero.
6.- Todo número positivo es mayor que cero.
7.- Todo número negativo es menor que cualquier número positivo.
Actividad 1.
1. Escribe en el cuaderno la respuesta a cada ejercicio utilizando el símbolo "<" o ">" en cada caso.
a) Ordena en forma creciente (de menor a mayor) los siguientes números:

b) Ordena en forma creciente los siguientes números:

c) Ordena en forma decreciente los siguientes números:

d) Ordena en forma creciente los siguientes números:

2. Juego: ordena los siguientes números como lo indica la actividad: al terminar enseña el resultado a tu docente
https://wordwall.net/es/resource/17970789/matem%c3%a1ticas/ordenar-n%c3%bameros-enteros
3. Indica que número es mayor o menor a través del juego en el siguiente link: (enséñale los resultados a tu docente).
https://wordwall.net/es/resource/17980935/matem%c3%a1ticas/comparaci%c3%b3n-de-n%c3%bameros-enteros
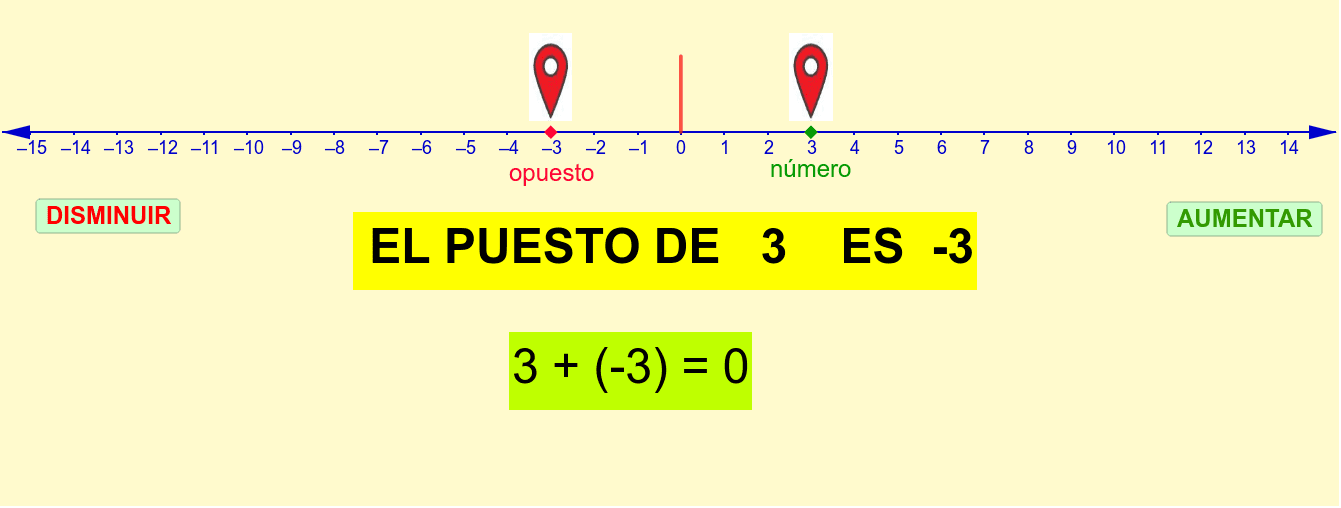
3. NÚMEROS OPUESTOS
Los números opuestos, son número que al ser sumados nos da como resultado el número 0.
El opuesto de un número tiene el mismo valor absoluto, pero con signo contrario.
EJEMPLO:

- +3 y −3 son números opuestos.
- +9.4 y −9.4 son números opuestos.
- +1/4 y −1/4 son números (fracciones) opuestos.
Actividad 2:
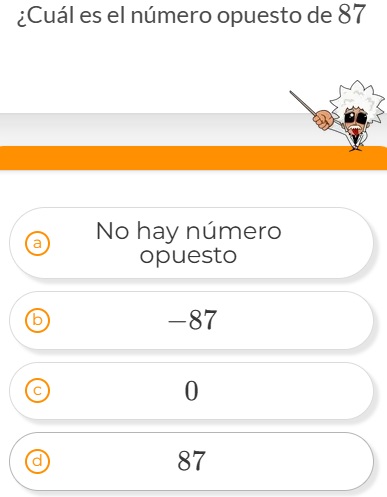
1. Colorea en tu cuaderno la respuesta correcta:

2. Realiza los ejercicios del siguiente enlace: https://es.khanacademy.org/math/cc-sixth-grade-math/cc-6th-negative-number-topic/cc-6th-number-opposites/e/number-opposites
4. VALOR ABSOLUTO
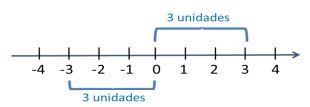
El valor absoluto de un número entero se define como la distancia en unidades de dicho número con respeto al cero.
Ejemplo:
En la gráfica vemos que la distancia de 3 y -3 hasta el punto 0 siempre va a ser 3 positivo. El valor absoluto corresponde a una distancia, por lo tanto siempre será positivo.
Actividad 3.
1. Completa en el cuaderno las siguientes oraciones sobre los números enteros.
a) El conjunto de los números enteros se simboliza con la letra ____________.
b) Los números negativos se encuentran a la __________________ del cero.
c) Los números positivos se encuentran a la __________________ del cero.
Respuestas de mayor, menor o igual
d) El número 2.345 es __________________ que el número –5.489.
e) El número 0 es _________________ que el número –267.
f) |24| es _____________________ |24|.
g) |-15| es ____________________ 0.
h) El antecesor de –9 es ___________________
i) El sucesor de –11 es ___________________ .
j) El antecesor de –15 es ___________________
k) |-15| es ____________________ |-20|.
l) El conjunto de los enteros se forma por tres subconjuntos: ______________________________.
m) El conjunto de los naturales N=____________.
n) El valor absoluto de un número es la ________________ entre dicho número y el cero. Por lo tanto, el valor absoluto de cualquier entero es siempre __________________.
2. Resolver los siguientes ejercicios de valor absoluto (en el cuaderno):
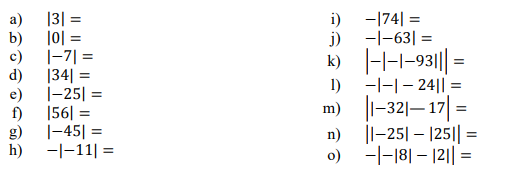
OPERACIONES CON NÚMEROS ENTEROS
1. ADICIÓN Y SUSTRACCIÓN:
Se distinguen dos casos:
a) Adición de enteros de igual signo: se suman sus valores absolutos y se conserva el signo.
Ejemplos: - 6 + - 4= - 10 (+)7 + (+8)= + 15 - 2 + - 12= - 14 (+ 12) + (+ 3)= + 15
b) Adición de enteros de distinto signo: se restan valores absolutos y se conserva el signo del número con mayor valor absoluto.
Ejemplo: (+ 10) + (- 40) = - 30 (+ 12) + (- 4) = 8 (- 11) + (+ 14)= 3 (- 40) + (+ 6) = - 4
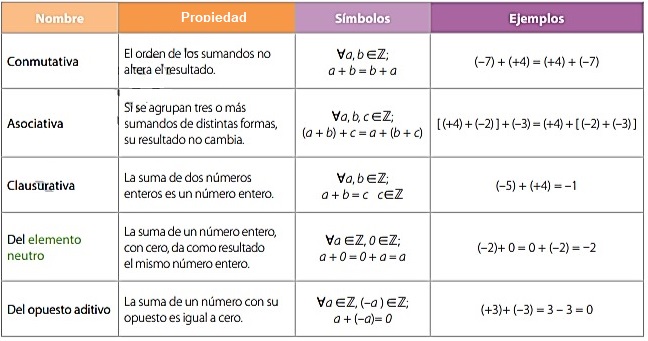
Propiedades de la adición y sustracción:
a) Conmutatividad: El orden del resultado no altera el producto. 𝑠𝑖 𝑎, 𝑏 ∈ ℤ ⇒ 𝑎 + 𝑏 = 𝑏 + 𝑎.
b) Asociatividad: Si se agrupan tres o más sumandos de distintas formas, su resultado no cambia. 𝑠𝑖 𝑎, 𝑏, 𝑐 ∈ ℤ ⇒ 𝑎 + 𝑏 + 𝑐 = 𝑎 + (𝑏 + 𝑐).
c) Clausurativa: La suma de dos números enteros da como resultado un entero. 𝑠𝑖 𝑎, 𝑏 ∈ ℤ ⇒ 𝑎 + 𝑏 ∈ ℤ.
d) Elemento neutro: La suma de un número entero con cero (0), da como resultado el mismo número entero. 𝑠𝑖 𝑎 ∈ ℤ ⇒ ∃! 0 ∈ ℤ 𝑡𝑎𝑙𝑞𝑢𝑒 𝑎 + 0 = 0 + 𝑎 = 𝑎.
e) Opuesto aditivo o inverso aditivo: La suma de un número con su opuesto es cero (0). 𝑠𝑖 𝑎 ∈ ℤ ⇒ ∃ − 𝑎 ∈ ℤ 𝑡𝑎𝑙𝑞𝑢𝑒 𝑎 + −𝑎 = −𝑎 + 𝑎 = 0.
Debido al cumplimiento de estas 5 propiedades, se dice que el conjunto de los números enteros con respecto a la adición tiene estructura algebraica de grupo abeliano o grupo conmutativo cuya notación es ℤ, + es grupo abeliano.
Ejercicio 4: Al finalizar enséñale el resultado al docente
1. Responde los ejercicios a través del juego en el siguiente link:
https://wordwall.net/es/resource/14759432/suma-y-resta-de-numeros-enteros
2. Responde los ejercicios a través del juego en el siguiente link:
https://wordwall.net/es/resource/15936691/suma-de-n%C3%BAmeros-enteros
3. Responde los ejercicios a través del juego en el siguiente link:
https://wordwall.net/es/resource/31793309/matem%c3%a1ticas/juego-de-operaciones-con-numeros-enteros

4. Reducir las siguientes expresiones (en el cuaderno):

2. MULTIPLICACIÓN:
se distinguen dos casos:
a) Multiplicación de números enteros de igual signo: el producto de dos números enteros de igual signo es un entero positivo, cuyo valor absoluto es igual al producto de los valores absolutos de los factores. Ejemplo: + 6 · + 4 = + 24 - 9 · - 4 = + 36
b) Multiplicación de números enteros de distinto signo: el producto de dos números enteros de distinto signo es un entero negativo, cuyo valor absoluto es igual al producto de los valores absolutos de los factores.
Ejemplo: - 12 · + 3 = - 36 + 11 · - 4 = - 44
Propiedades de la multiplicación:
a) Clausurativa: 𝑠𝑖 𝑎, 𝑏 ∈ ℤ ⇒ 𝑎 ∙ 𝑏 ∈ ℤ.
a) Conmutatividad: 𝑠𝑖 𝑎, 𝑏 ∈ ℤ ⇒ 𝑎 ∙ 𝑏 = 𝑏 ∙ 𝑎.
b) Asociatividad: 𝑠𝑖 𝑎, 𝑏, 𝑐 ∈ ℤ ⇒ 𝑎 ∙ 𝑏 ∙ 𝑐 = 𝑎 ∙ (𝑏 ∙ 𝑐).
e) Elemento neutro: 𝑠𝑖 𝑎 ∈ ℤ ⇒ ∃! 1 ∈ ℤ 𝑡𝑎𝑙𝑞𝑢𝑒 𝑎 ∙ 1 = 1 ∙ 𝑎 = 𝑎.
e) Propiedad distributiva de la multiplicación con respecto a la adición:
𝑠𝑖 𝑎, 𝑏, 𝑐 ∈ ℤ ⇒ 𝑎 ∙(𝑏 + 𝑐) = 𝑎 ∙ 𝑏 + 𝑎 ∙ 𝑐.
El conjunto de los números enteros, con las operaciones de la multiplicación y adición, tiene estructura algebraica de anillo conmutativo con unidad, cuya notación es: ℤ , +,∙ es anillo conmutativo con unidad.

Ejercicio 5:
1. Resolver las siguientes multiplicaciones en ℤ:
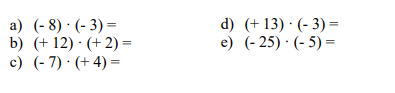
2. Responde las siguientes preguntas a través del juego en el siguiente link: (Al terminar enséñale los resultados a tu docente)
https://wordwall.net/es/resource/23778681/multiplicacion-de-numeros-enteros
3. DIVISIÓN:
Se distinguen dos casos:
a) División de números enteros de igual signo: el cociente de dos enteros de igual signo es un número positivo.
Ejemplos: + 18 : + 9 = + 2 - 90 : - 2 = + 45
b) División de números enteros de distinto signo: el cociente de dos enteros de distinto signo es un número positivo.
Ejemplos: + 12 : - 6 = - 2 - 40 : + 4 = - 10
NOTA: para resolver un ejercicio en el que aparecen varias operaciones, se debe resolver respetando la prioridad de las operaciones:
1° Paréntesis.
2° Potencias.
3° Multiplicaciones y divisiones (de izquierda a derecha)
4° Adiciones y sustracciones (de izquierda a derecha)
Para reforzar el tema te invito a observar el siguiente video:
o éste otro video:
Ejercicio 6:
1. Resolver las siguientes divisiones en ℤ:
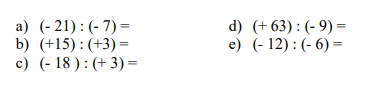
2. Resolver los siguientes ejercicios de operaciones combinadas:
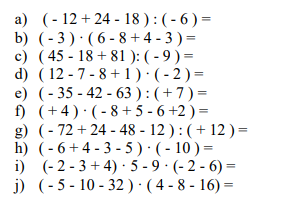
3. Realiza los siguientes ejercicios de división a través del juego:
https://wordwall.net/es/resource/14921934/division-de-numeros-enteros
Nota: Los siguientes ejercicios pueden ser creado por el docente en https://quizizz.com/ y realizar un fogueo en línea entre entudiantes o en su defecto pueden utilizar los siguientes ya creados:
4. Resolver los siguientes problemas de números enteros:
a) En invierno en cierto lugar del sur de Chile la temperatura a las 16 horas fue de 12°C. A las 3 de la mañana hubo un descenso de 17°C. ¿Cuál fue la temperatura registrada a esa hora?
b) Santiago tuvo ayer una temperatura de 7º C bajo 0 en la mañana y en la tarde subió 18ºC. ¿Cuál fue la temperatura alcanzada?.
c) Una sustancia química que está a 5°C bajo cero se calienta en un mechero hasta que alcanza una temperatura de 12°C sobre cero. ¿Cuántos grados subió?
d) María deposita el lunes, en su libreta de ahorros, cuyo capital ascendía a $56.000, la cantidad de $12.670. El día miércoles por una urgencia, realiza un giro de $123.000. ¿Cuál es el nuevo capital que posee?. Escribe la operación utilizando números enteros.
e) ¿Cuántos años transcurrieron desde la muerte de Julio César ( año 44 A.de C.) hasta la caída del Imperio Romano de Occidente ( año 395 D. de C.)
f) Euclídes, geómetra griego, nació en el año 306 A de C y murió en el año 283 A. de C. ¿Qué edad tenía cuando murió?
g) En Calama la temperatura de hoy fue de 8º sobre 0 en la tarde y 5º bajo 0 en la noche. ¿En cuántos grados varió la temperatura?
h) Un auto está ubicado a 7 m. a la derecha de un punto A, luego avanza 23 m., retrocede 36m.vuelve avanzar 19 m. y retrocede 36 m. ¿A qué distancia del punto A se encuentra?
i) ¿Cuál es la diferencia de nivel entre un punto que está a 1.500 metros sobre el nivel del mar y otro que está a 300 metros bajo el nivel del mar?
j) Dada la siguiente serie numérica: ... –7, -4, -1, 2, 5, ... ¿Cuál es la suma del número entero anterior a –7 con 5?
k) En la primera parada de un bus suben 7 personas, en la segunda suben 5 y bajan 2, en la tercera suben 9 y baja 1, en la cuarta parada baja la mitad de los pasajeros. ¿Cuántos pasajeros quedan en el bus?
l) Un submarino de la flota naval, desciende a 50 metros bajo el nivel del mar y luego asciende a 20 metros. Entonces queda a una profundidad de:
m)Una persona ha realizado dos giros, de $4.000 y $15.000 en su cuenta bancaria, quedando con un saldo de - $12.000 en su cuenta. ¿Cuánto dinero tenía antes de realizar los dos giros?
n) El Aconcagua es el cerro más alto de la cordillera de los Andes con una altura de 6.959 m sobre el nivel del mar. Por otra parte, la fosa de Atacama tiene una profundidad aproximada de 8.000 m. Responde.
i. ¿Cuál es la distancia entre la cima del Aconcagua y la profundidad de la fosa de Atacama?
ii. Supón que el Aconcagua estuviera apoyando su base sobre la fosa de Atacama. ¿Aparecería la cumbre sobre el nivel del mar? ¿A qué distancia del nivel del mar quedaría la cumbre?
o) El recorrido de un caracol al subir una muralla es el siguiente: sube 3 metros y baja 2 metros. Si la muralla tiene 10 metros de altura ¿cuánto recorre el caracol para llegar a la cima de la muralla?
i. Expresa la suma de las distancias recorridas con números enteros.
ii. Expresa la suma de las distancias con valores absolutos y calcula el recorrido total del caracol.
p) Un buzo bajó 24 metros en 4 horas a una velocidad constante. ¿Cuántos metros bajó en cada hora? Al transcurrir 3 horas, ¿a cuántos metros del nivel del mar estaba el buzo?
q) Felipe, pide su estado de cuenta en un cajero automático, en él se indica que debe $ 96.000 de su línea de crédito. Se sabe que en los últimos 4 días retiró la misma cantidad de dinero y no se realizaron otros movimientos en su cuenta.
i. ¿Cuánto dinero retiró cada día?
ii. Al tercer día, ¿cuánto dinero había ocupado de su línea de crédito?
r) Pedro, al ir del colegio a su casa, decidió jugar, que por cada 6 pasos que caminara, iba a retroceder 2, a lo cual llamó "una jugada". Suponiendo que cada paso mide lo mismo, 130 cm,
a) ¿Cuánto avanza si lleva 5 jugadas?
b) ¿Cuál es la distancia entre el colegio y su casa, si para llegar de una a otro debe realizar 120 jugadas?
s) Sócrates, filósofo griego, nació en el año 470 a.c. y murió envenenado en el año 399 a.c. Tiberio, emperador romano, que estaba en el poder al nacimiento de Cristo nació en el año 42 a.c. y murió en el año 37 d.c.
i. ¿A qué edad murió Sócrates?
ii. ¿Cuántos años vivió el emperador Tiberio?
iii.¿Qué edad tenía Tiberio en el año que nació Cristo?
iv. ¿Cuántos años hay entre los nacimientos de Sócrates y Tiberio?
t) En el planeta Marte, en las regiones más cálidas, a mediodía hay una temperatura ambiente de 25ºC aproximadamente, pero en la noche la temperatura puede descender a -66ºC. ¿Cuál es la oscilación térmica entre el día y la noche en Marte?
u) La temperatura de la superficie de una nave espacial al entrar en la atmosfera varía de -200ºC a 2.300ºC en diez minutos.
i. ¿Cuántos grados aumenta, en promedio, por minuto?
ii. ¿Qué temperatura tiene la nave a cabo de 3 minutos?
v) Al comenzar la semana, la señora María, dueña de una panadería, fue a comprar los insumos para hacer queques, llevando todo el dinero que tenía. Compró harina, y le quedó debiendo al proveedor $27.091. Luego, fue a cobrar un dinero que le debían por una trotas. Eran $41.900. Pagó la deuda con el proveedor de harina y luego compró margarina y leche por un total de $ 65.078 y polvos de hornear a $3.846, quedando debiendo ambas cantidades. Al final de la semana, recolecto $93.875. Pagó su deuda y quedo con $52.814. ¿Cuánto dinero tenía al iniciar la semana?
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
ACÁ PUEDES DESCARGAR LA GUÍA
ACUERDOS PEDAGÓGIOS
RÚBRICA
Operaciones con números enteros:
Rúbrica números opuestos:
Rubrica valor absoluto: