Grado 6 - Periodo 3

TEMAS: NÙMEROS DECIMALES

1- Concepto, notación, 2. Clasificación de decimales, 3. Aproximaciones de números decimales (redondeo, truncamiento), 4. Operaciones básicas, (adición, sustracción, multiplicación, división), 5. Regla de tres simple

DBA 1. Comprende y resuelve problemas, que involucran los números racionales con las operaciones (suma, resta, multiplicación, división, potenciación, radicación) en contextos escolares y extraescolares

DBA 2. Describe y utiliza diferentes algoritmos, convencionales y no convencionales, al realizar operaciones entre números racionales en sus diferentes representaciones (fracciones y decimales) y los emplea con sentido en la solución de problemas. 

Conocimientos previos: Operaciones básicas (Suma, resta, multiplicación, división) de naturales

Suma y resta

Multiplicación y división:

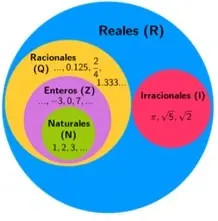
RECORDEMOS: Los números reales están conformados por números racionales e irracionales.

Los racionales (Q) a su vez se componen de fraccionarios y decimales, (enteros y naturales)

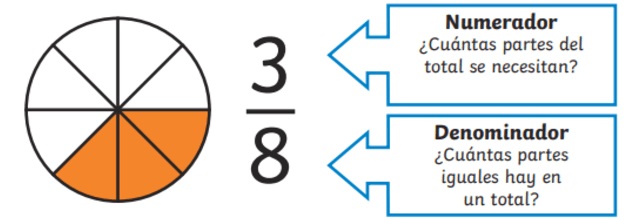
Ya vimos que los fraccionarios son aquellos que tienen la forma de fracción:

1. CONCEPTOS BÁSICOS DE LOS NÚMEROS DECIMALES

Los números decimales constan de dos partes: * parte entera y * parte decimal separadas por un punto o una coma decimal, dependiendo del país donde te encuentres.

Ejemplo:

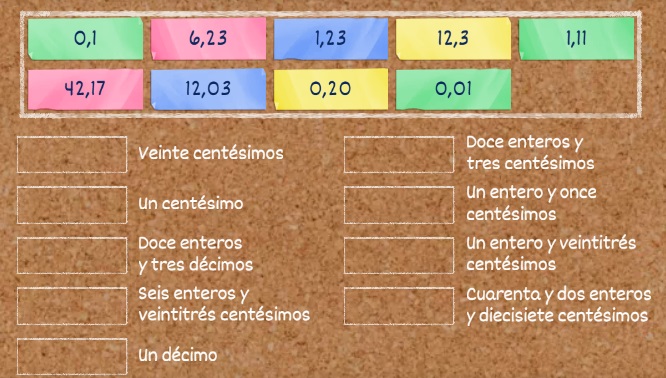
¿Como se leen los números en la parte entera y decimal de acuerdo a su posición?

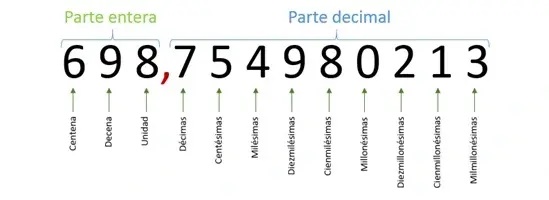
Primera forma de leer el número:

1. Lee la parte entera de izquierda a derecha seguida de la palabra "enteros".
2. Lee toda la parte decimal como se lee la parte entera.
3. Menciona la posición en la que se encuentra la última cifra decimal.

Entonces, el número 698,754980213 se lee "seiscientos noventa y ocho enteros setecientos cincuenta y cuatro millones novecientos ochenta mil doscientos trece milmillonésimas".

Segunda forma de leer el número:

1. Lee la parte entera de izquierda a derecha seguida de la palabra "coma".
2. Lee toda la parte decimal como se lee la parte entera.

De esta manera, el número 698,754980213 se lee "seiscientos noventa y ocho coma setecientos cincuenta y cuatro millones novecientos ochenta mil doscientos trece".

VIDEO:

Si quieres reforzar más el tema te invito a observar el siguiente video:

https://www.youtube.com/watch?v=bVFExqCCwfE 

Realiza la siguiente actividad interactiva (Juegos):

https://wordwall.net/es/resource/4163160/lectura-y-escritura-de-decimales

ACTIVIDAD 1 (En el cuaderno)

1. Utiliza el primer método para leer estos números decimales y escríbelos en tu cuaderno:

• 456,268435
• 35.413,9346103
• 58,79516428

2. Realiza la práctica interactiva de la siguiente página: https://wordwall.net/es/resource/7768918/lectura-y-escritura-de-decimales y muéstrale los resultados a tu docente.

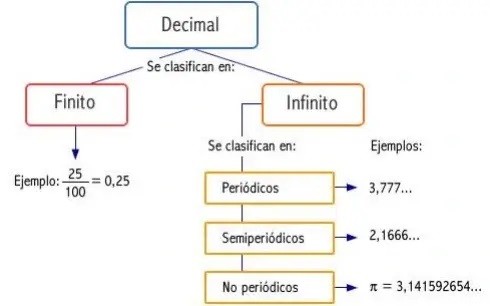
2. CLASIFICACIÓN DE DECIMALES

Los números decimales los podemos clasificar en:

• Decimales finitos o exactos: tienen un número concreto de cifras decimales.
• Decimales infinitos: su parte decimal no termina, no tiene fin.

Dentro de estos últimos podemos distinguirlos en:

• Periódicos puros: Toda su parte decimal se repite periódicamente.
• Periódicos mixtos o semiperiódicos: Dentro de su parte decimal hay unas cifras que no se repiten y otras que se repiten periódicamente.
• No periódicos: Su parte decimal es infinita pero sus cifras no se repiten periódicamente.

VIDEO:

Si quieres reforzar más el tema sobre clasificación de decimales te invito a observar el siguiente video:

https://www.youtube.com/watch?v=PZOgxa-gJ90

Como ordenar números infinitos periódicos y mixtos:

https://recursos.edu.xunta.gal/sites/default/files/recurso/1606139639/Ordenacion_decimales.mp4 

ACTIVIDAD2 (En el cuaderno):

1. Indica al frente que tipo de decimal es:

• 2,2 =
• 3,457777777.... =
• 86,8756473829.... =
• 9,99999999.... =
• 3,21 =
• 3,45678... =
• 8,81818181.... =
• 0,21837629 =
• 0,2188888... =
• 0,222222... =

2. Realiza la siguiente actividad a través del juego de la lectura y escritura de decimales:

https://wordwall.net/es/resource/4163160/lectura-y-escritura-de-decimales 

3. APROXIMACIÓN DE DECIMALES

3.1. Redondeo

Todo número decimal puede ser redondeado. El redondeo se refiere a reducir la cantidad de cifras de un número para tener un valor similar. Las reglas son las siguientes:

• Redondeo por defecto: si la última cifra del número que deseamos redondear es 1, 2, 3 o 4, la sustituimos por 0, y no variamos la penúltima cifra. Por ejemplo, el número 18,3

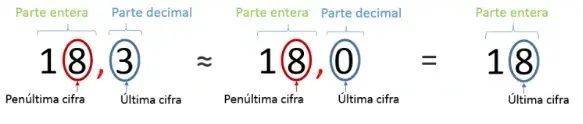
3.2. Truncamiento

También llamado redondeo por exceso.

Si la última cifra es 5, 6, 7, 8 o 9, también sustituimos por 0 pero en este caso aumentamos la penúltima cifra en 1. Por ejemplo, el número 45,8.

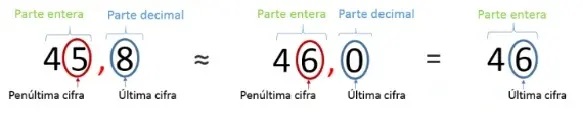
Podemos aproximar los números decimales a la unidad más cercana, es decir, acercarlo a un número de la recta numérica que tenga menos decimales que este por medio de las mismas reglas. También los podemos aproximar a las décimas, centésimas, milésimas, etc., más cercanas. Por ejemplo, observa los siguientes números y redondéalos: 18,82653 y 45,73286.

El primer número lo aproximamos mediante la regla de redondeo por defecto, ya que la última cifra está entre 0 y 4. Aquí la cifra se aproximó a la diezmilésima más cercana.

Y para el segundo número seguimos la regla de exceso, ya que la última cifra está entre 5 y 9. Aquí la cifra se aproximó a la a la diezmilésima más cercana.

ACTIVIDAD 3 (En el cuaderno):

I. Convierte los siguientes números decimales a enteros por redondeo:

1. 84,91
2. 14,3
3. 9.214,12
4. 465,568
   

II. Aproxima estos números a las décimas, centésimas o milésimas más cercanas:

1. 486,945 (Décima):
2. 45,87 (Centésima):
3. 326,3462 (Milésima):
   

III. Realiza truncamiento o redondeo de acuerdo con la posición decimal dada en el ejercicio:

1. Truncamiento a las décimas de: 8,538
2. Aproximación a las milésimas de: 6,345734
3. Aproximación a las centésimas de 4,43923
4. Truncamiento a las milésimas de: 1,23434

IV. Realiza los ejercicios "jugando" en el siguiente link:

https://wordwall.net/es/resource/7460488/n%c3%bameros-decimales/decimales

NOTA: Si tienes dudas del tema, revisar el siguiente video:

https://www.youtube.com/watch?v=Om9NP_TJKEU

Exploración de Saberes Previos:

Conversión de un decimal a fracción: Para convertir un decimal a fracción decimal, se escribe como numerador el número decimal, sin la coma. Como denominador, se escribe el 1 seguido de tantos ceros como cifras decimales tenga el número decimal. Ejemplos:

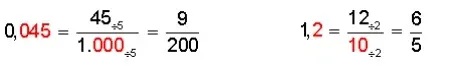
Conversión de una fracción decimal a NÚMERO decimal: para convertir una fracción decimal a número decimal, se escribe el numerador de la fracción y se desplaza la coma, desde las unidades, tantos lugares a la izquierda como ceros tenga el denominador

4. OPERACIONES CON DECIMALES

A) SUMA: 

Para sumar dos o más números decimales se colocan en columna haciendo coincidir las comas; después se suman como si fuesen números naturales y se pone en el resultado la coma bajo la columna de las comas.

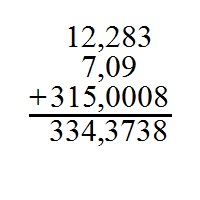
B) RESTA: Para restar números decimales se colocan en columna haciendo coincidir las comas. Si los números no tienen el mismo número de cifras decimales, se completan con ceros las cifras que faltan. Después, se restan como si fuesen números naturales y se pone en el resultado la coma bajo la columna de las comas.

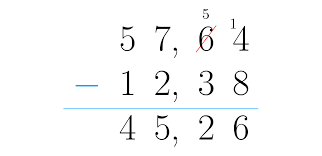
C) MULTIPLICACIÓN: Para multiplicar dos números decimales se efectúa la operación como si fuesen números naturales y en el producto se separan tantas cifras decimales como cifras decimales tengan entre los dos factores.

D) DIVISIÓN: Para dividir un número decimal por un número natural se hace la división como si fuesen números naturales, pero se pone una coma en el cociente al bajar la primera cifra decimal.

División de un número natural por un decimal: Para dividir un número natural por un número decimal se suprime la coma del divisor y a la derecha del dividendo se ponen tantos ceros como cifras decimales tenga el divisor. Después se hace la división como si fuesen números naturales

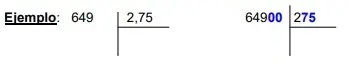
División de dos números decimales: Para dividir dos números decimales se suprime la coma del divisor y se desplaza la coma del dividendo tantos lugares a la derecha como cifras decimales tenga el divisor; si es necesario, se añaden ceros.

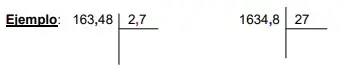
RESUMEN DE APOYO AL TEMA DECIMALES - VÍDEOS RECOMENDADOS:

Observa estos vídeos que te ayudarán a aprender y afianzar los conceptos básicos y operaciones con decimales:

Conceptos básicos decimales: https://youtu.be/mTwHR7LkE_U

Clasificación de los decimales: https://youtu.be/s_VPifmsfxY

Comparación de decimales: https://youtu.be/TY7ffZg7RWo

Suma y resta con decimales: https://youtu.be/06VFoIqDELA

Multiplicación decimales: https://youtu.be/W7qSmEtSrYU

APLICACIÓN:

NOTA: Todo el taller se desarrolla en el cuaderno; mostrar proceso y dar claramente la(s) respuesta(s).

Trabajar ordenadamente.

ACTIVIDAD 4 (En el cuaderno):

Para cada ejercicio realice el proceso que justifique su respuesta.

1) ¿Qué lugar ocupan las milésimas en un número decimal? ¿Y las centésimas?

2) Encerrar con color rojo la cifra de las centésimas y con color azul la cifra de las milésimas.

1,256 32,325                     6,3248                                514,3207

3,641                                 0,003                                 0,0341                            40,1239

3) Encerrar con círculo de color rojo la parte entera y con un círculo de color azul la parte decimal.

3,25                                  2,64                                    5,2                                 0,27                                 0,4

6. REGLA DE TRES SIMPLE

En la regla de tres simple, se establece la relación de proporcionalidad entre dos valores conocidos A y B, y conociendo un tercer valor X, calculamos un cuarto valor Y.

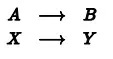
La regla de tres simple es una herramienta matemática que sirve para resolver rápidamente problemas que involucran una relación de proporcionalidad directa entre dos variables. 

REGLA DE TRES DIRECTA o INVERSA

La relación de proporcionalidad puede ser directa o inversa. Será directa cuando a un mayor valor de A habrá un mayor valor de B, y será inversa cuando a un mayor valor de A corresponda un menor valor de B.

Donde k es la constante de proporcionalidad. Para que esta proporcionalidad se cumpla se tiene que a un aumento de A le corresponde un aumento de B en la misma proporción. Se puede representar de la forma:

Se dice entonces que A es a B directamente proporcional, como X es a Y, siendo Y igual al producto de B por X dividido entre A. Imaginemos que se nos plantea lo siguiente:

Este problema se interpreta de la siguiente manera: la relación es directa, dado que, a mayor número de habitaciones hará falta más pintura, y lo representamos así:

Ejemplo 1:

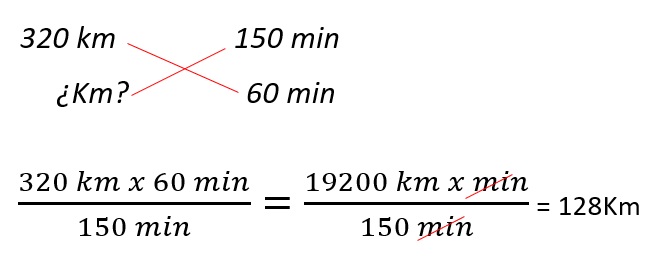
Una motocicleta recorre 320 kilómetros en 150 minutos, ¿a cuántos kilómetros por hora viajó?

ASPECTOS A TENER EN CUENTA: 

1. Debemos trabajar las mismas unidades de media, bien sea en horas o en minutos, 

2. Las unidades deben ser iguales por columna, 

3. A veces nos toca replantear el ejercicio o la pregunta.

4. Por lo general donde va el signo de pregunta se coloca una "X" como incógnita, en los próximos ejercicios la colocaremos.

El ejercicio quedaría planteado de la siguiente forma:

Una motocicleta recorre 320 kilómetros en 150 minutos, ¿en 60 minutos cuántos kilómetros viajó?

En este caso multiplicamos en cruz 320 x 60 y luego dividimos entre 150, de la siguiente manera:

Ejemplo 2:

Este año hubo 42 días con lluvias, ¿Qué porcentaje del año significa eso?

NOTA: En este ejercicio aparentemente nos dan 1 solo dato, pero en la pregunta nos obligan a replantear diciendo: "360 días corresponden al 100% que porcentaje corresponde a 42 días?"

Corresponde al 11,7%

Ejemplo 3:

En 50 litros de agua de mar hay 1300 gramos de sal, ¿en cuántos litros estarán contenidos 11600 gramos?

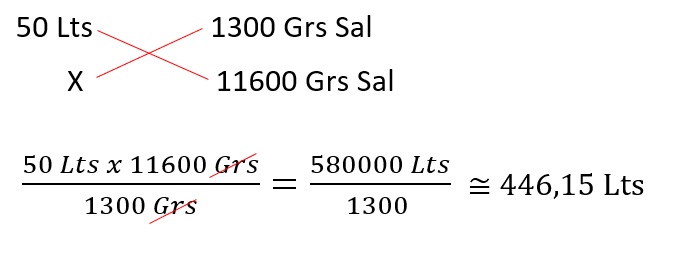
En 446,15 Lts de agua de mar contienen 11.600 Grs de sal

ACTIVIDAD5 (En el cuaderno):

1. Si en dos horas y media un motociclista ha cubierto una distancia de 320 kilómetros. ¿Ha superado el límite de velocidad previsto, que es de 80 km/h?
2. Si debo sembrar 30 semillas de maíz por surco, ¿Cuántos semillas necesitaré para dejar sembrado un lote de 20 surcos?
3. Tres canillas tardan 10 horas en llenar un depósito de agua. ¿Cuántas horas tardarán 5 canillas en hacerlo?
4. Con 5 litros de pintura se han pintado 90 m de verja. Calcular cuántos metros de verja se podrán pintar con 30 litros.
5. Si una persona puede vivir en Nueva York durante 10 días con 650 dólares. ¿Cuántos días podrá costearse si solo tiene 500 dólares?
6. Una máquina fabrica 1200 tornillos en seis horas, ¿Cuánto tiempo le llevará a la máquina fabricar 10000 tornillos?
7. Con cuarenta horas semanales de trabajo, un trabajador ganó $12000, ¿Cuánto ganará si la semana siguiente puede trabajar cincuenta horas?

Fuente: https://www.ejemplos.co/20-ejemplos-de-regla-de-tres-simple/#ixzz7XNbyLRIN