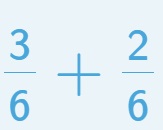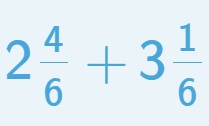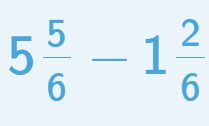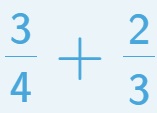Grado 6 - Periodo 2

Matemáticas

Temas:

TEORIA DE NÚMEROS                                                               NUMEROS FRACCIONARIOS      

• Múltiplos y Divisores de Números Naturales.        > Concepto de fracción
• Números Primos y Números Compuestos.            > Representación gráfica de facciones.
• Máximo Común Divisor (MCD)                                > Clases de fracciones 
• Mínimo Común Múltiple (mcm)                               > Operaciones con Números Fraccionarios

DBA 1. Interpreta los números enteros y racionales (en sus representaciones de fracción y de decimal) con sus operaciones, en diferentes contextos, al resolver problemas de variación, repartos, particiones, estimaciones, etc. Reconoce y establece diferentes relaciones (de orden y equivalencia y las utiliza para argumentar procedimientos). 

Estándar básico de competencia: Utilizo números racionales, en sus distintas expresiones (fracciones, razones, decimales o porcentajes) para resolver problemas en contextos de medida.

Saberes Previos: Manejo de operaciones matemáticas básicas, números primos. Te invito a observar el siguiente video, para que recuerdes lo que son números primos:

1. MÚLTIPLOS Y DIVISORES DE NÚMEROS NATURALES

Múltiplos de un número:  son todos los números naturales que se obtienen a multiplicar dicho número por todos los números naturales, incluyendo el cero. 

Ejemplo: "Para encontrar los múltiplos del '7', multiplicamos el '7' por todos los números naturales: 

7x1 = 7; 7x2=14; 7x3=21…, así hasta el infinito. 

Para saber si un número es múltiplo de otro: Dividimos el número que queremos saber si es múltiplo entre el otro (para ver si está en su "tabla"). 

Ejemplo: "Para saber si el número 5'739.024 es múltiplo de '8', dividimos ese número entre '8' el cual es igual a 717.378, por tanto, como su división es exacta, ese número es múltiplo de '8'. 

El conjunto de los múltiplos de un número a, se simboliza M(a). 

Ejemplo: Determina los múltiplos de 5, Expresa como conjunto los múltiples pedidos. 

M (5) = {0, 5, 10, 15, 20, 25, …}

2. MÍNIMO COMÚN MÚLTIPLO (m.c.m.) 

NOTA: Para entrar en el tema, debemos saber que este proceso se realiza con la comparación entre 2 o más números.

Ahora sí, daremos la definición:

El mínimo común múltiplo de dos o más números naturales es el menor múltiplo común de todos ellos. Este concepto está ligado con las fracciones de números naturales, es el número más pequeño de los múltiplos comunes. 

Ejemplo 1:

Primera forma:

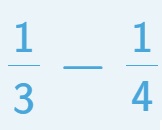
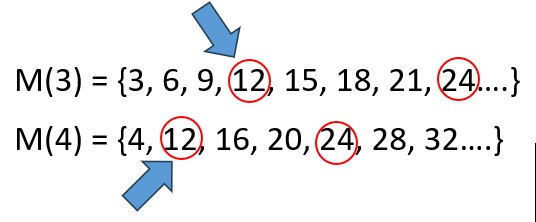
Hallar el mínimo común múltiplo de 3 y de 4

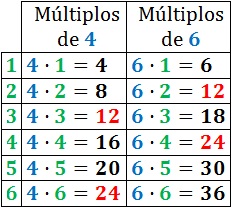
En este caso colocamos todos los múltiplos tanto de 3 como de 4:

Seleccionamos el menor que se repite entre ellos (en este caso 12):

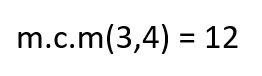
Segunda forma: 

Cuando los números son grandes es difícil realizarla de la primera forma, por tanto, debemos emplear esta segundo: 

Colocamos los números en tres columnas y trazamos una raya al final y los descomponemos (comenzando por el primer número primo que es el 2):

NOTA: Si el número a descomponer no se puede dividir, se baja tal cual el número, como en la tercera línea el 15 y el 9.

Luego multiplicamos los resultados dados al costado de la línea roja: 2 x 2 x 3 x 3 x 5 = 180

Es decir, el m.c.m(30,12,18) = 180

Sino comprendiste el tema te invito a observar el siguiente video:

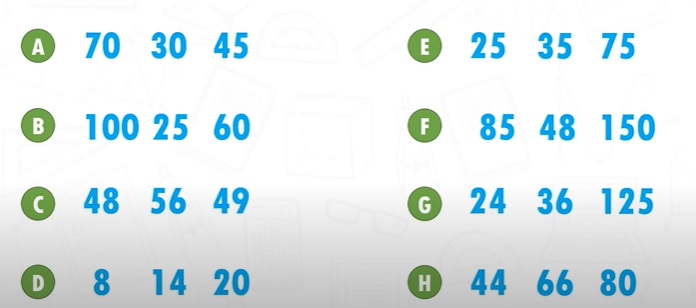
Actividad 1: Sacar el m.c.m de los siguientes números que aparecen al final del video:

3. MÁXIMO COMÚN DIVISOR

Se define el máximo común divisor de dos o más números enteros al mayor número entero que los divide sin dejar residuo alguno.

Ejemplo 1: Hallar el MCD de 12 y 16

Primera forma:

Como primera medida sacamos el listado de todos los números que se pueden dividir por 12 y 16:

Los números que se repiten son 1, 2, 4

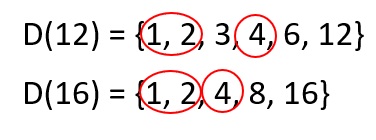
De allí sacamos el máximo de los que se repiten, es decir, 4, por tanto:

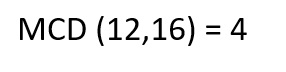
Ejemplo 2: Hallar el MCD de 12, 20 y 24

Segunda forma:

Como primera medida descomponemos cada número en factores primos:

Verificamos qué números se repiten en las 3 columnas. En este caso: dos veces 2 y lo multiplicamos. (2x2=4).

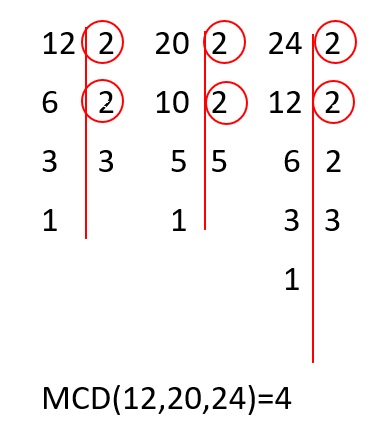
Por tanto, el número más grande que divide a estos 3 números es el 4. 

MCD (12, 20, 24) = 4

Si se te dificultó el tema, te invito a observar el siguiente video:

Ejercicio 2: 

Sacar el MCD de los siguientes números que aparecen al final del video:

Concepto de; NÚMEROS PRIMOS Y NÚMEROS COMPUESTOS

Para comprender mejor el tema te invitamos a observar el siguiente vídeo:

NÚMEROS FRACCIONARIOS

4. ¿Qué es una fracción?

Es cuando a un elemento completo le tomamos una parte o una porción. Por ejemplo:

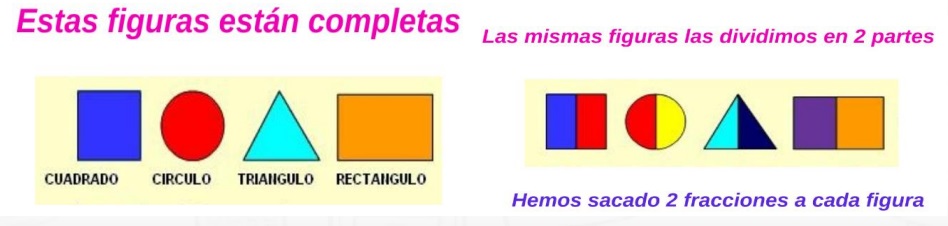
Podemos dividir las mismas figuras en 3 partes:

4.1. Partes de una fracción:

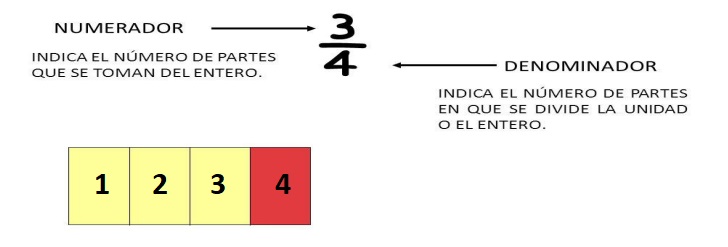
Ejemplo gráfico (lo que tomamos o sea el numerador, está en rosado):

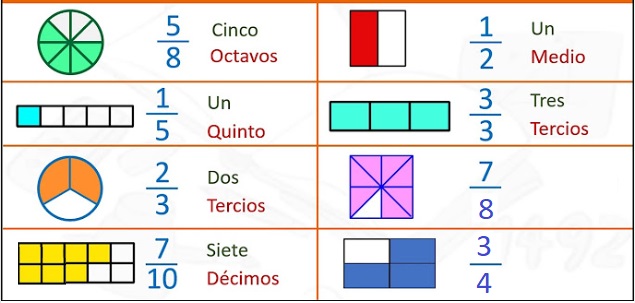
Lectura o pronunciamiento de la fracción:

4.2. Clasificación de las fracciones:

a. Fracciones Homogéneas: 

Son aquellas que tienen el mismo denominador, eso quiere decir que están divididas por el mismo número de partes:

b. Fracciones Heterogéneas:

Se presenta cuando los números de los denominadores son diferentes, eso quiere decir que están divididos en diferentes números de partes

c. Fracciones Impropias:

Son aquellas en las que el numerador es mayor o igual que el denominador, por ejemplo:

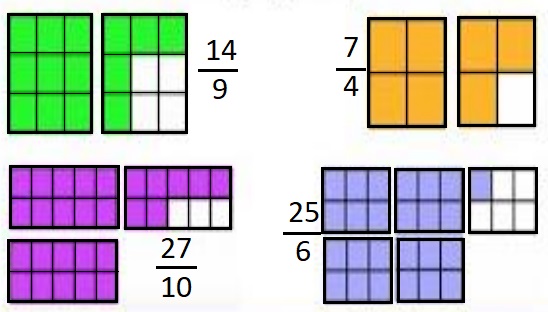
NOTA: Como el numerador es más grande copiamos la misma figura (con el número de casillas del denominador) tantas veces hasta llenar o completar el número dado en el numerador.

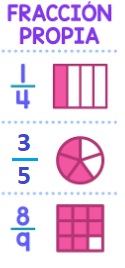
d. Fracciones Propias:

Son aquellas cuyo numerador es más pequeño que el denominador

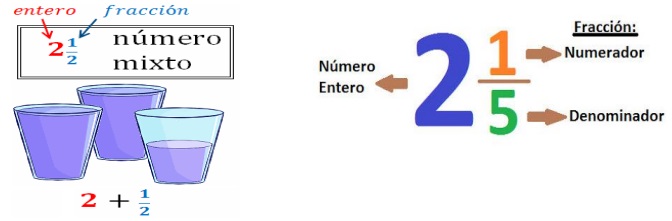
e. Fracciones Mixtas:

Están formados por un número entero y una fracción.

Ejercicio 3: (Para realizar en el cuaderno)

1. ESCRIBE al frente como se lee la fracción:

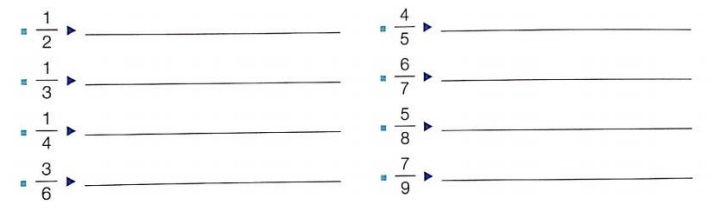
2. Utiliza la regla y divide la figura según te indica cada fracción. Colorea 

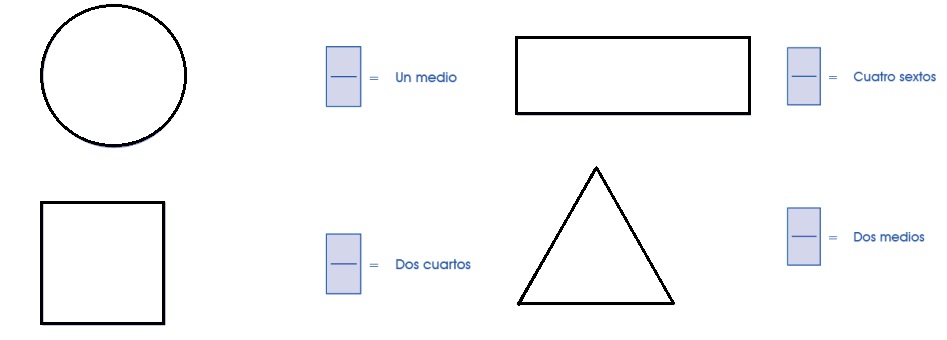
3. Une la fracción con la gráfica y al frente escribe como se lee. 

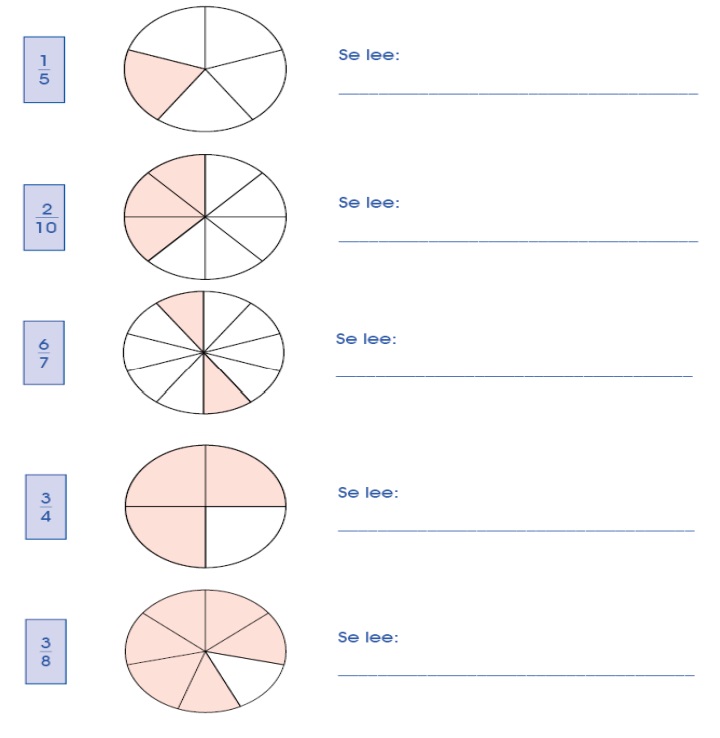
4. Escribe la fracción que representa la parte coloreada 

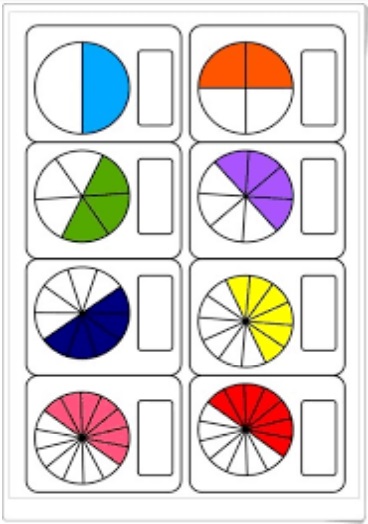
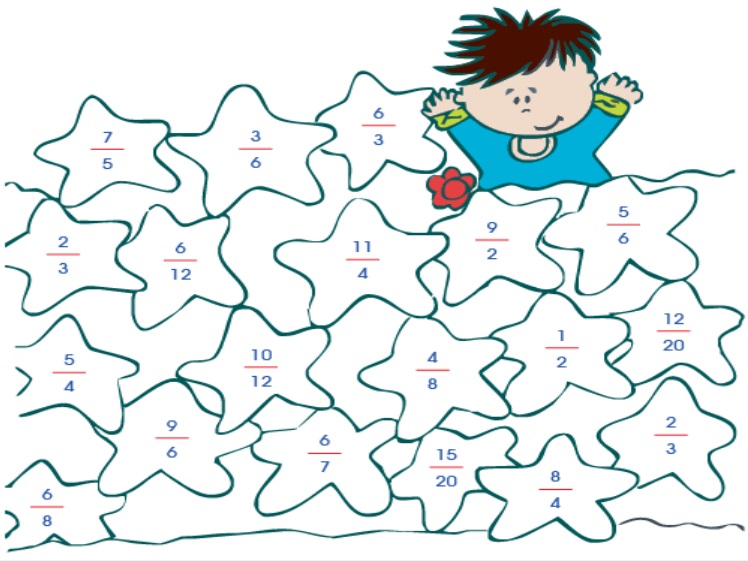
5.. Colorea de rojo, las estrellas con fracciones impropias y de amarillo, las estrellas con fracciones propias. 

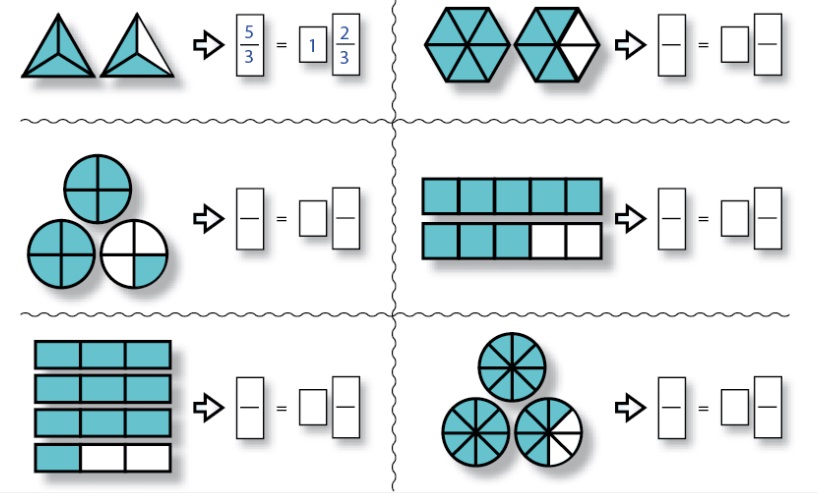
6.Escribe la fracción impropia y el número mixto que corresponde en cada caso. 

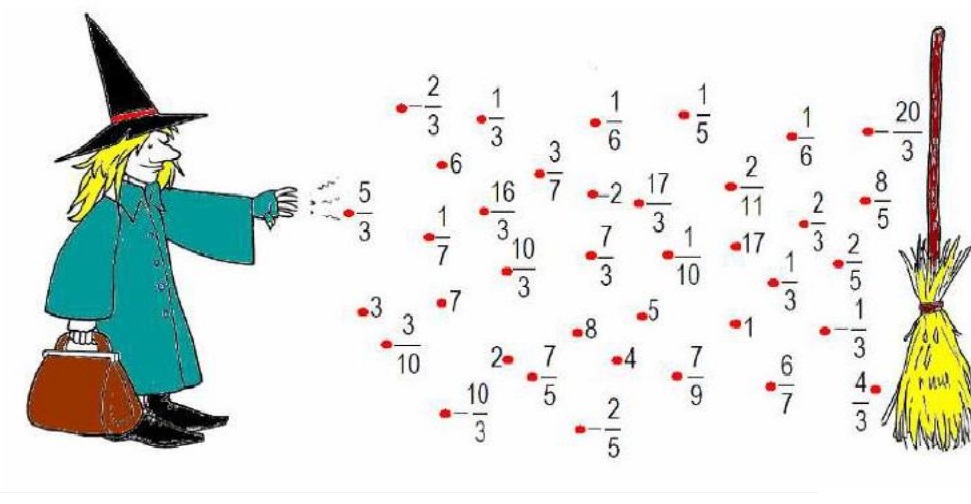
7.Observa la gran cantidad de fracciones que tiene la brujita. Toma de allí algunas fracciones y completa los cuadros. 

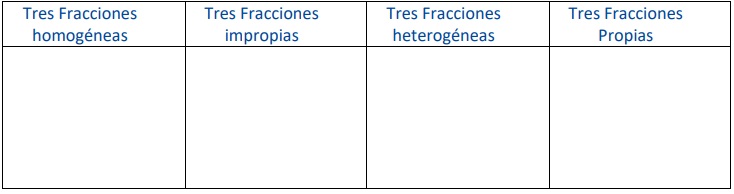
8. Escribe las fracciones que representa la parte pintada y clasifícalas en propias e impropias: 

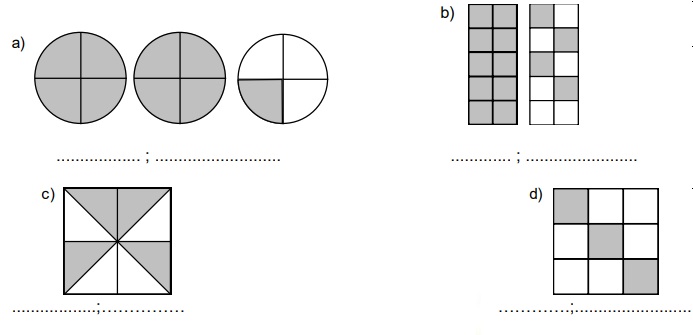
OPERACIONES CON NÚMEROS FRACCIONARIOS

A. SUMA Y RESTA

 Tomado de: https://www.sev.gob.mx/matematicas/mateminis/suma-y-resta-de-fracciones/ 

Los diversos procedimientos para realizar sumas de fracciones también pueden aplicarse a las restas, usa el que te sea más sencillo. 

Suma de 3 fracciones - 1ra forma:

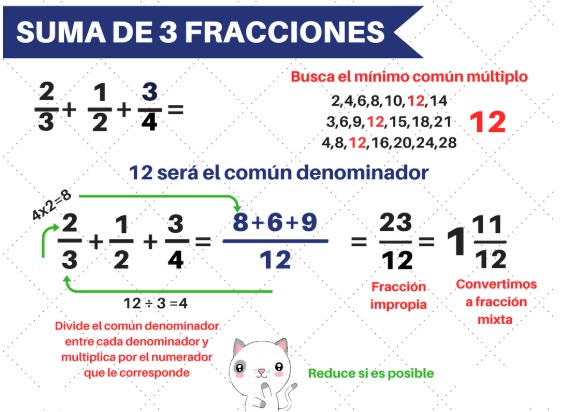
Suma de 3 fracciones - 2da forma:

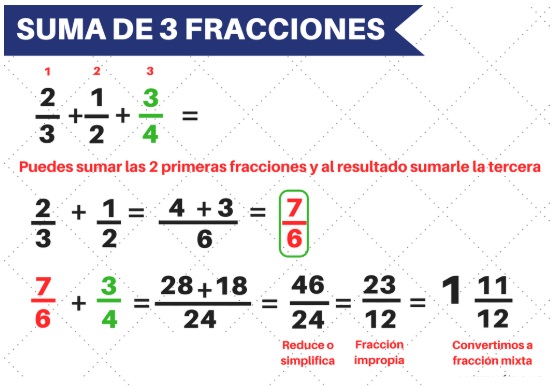
Suma de fracciones mixtas 1ra forma:

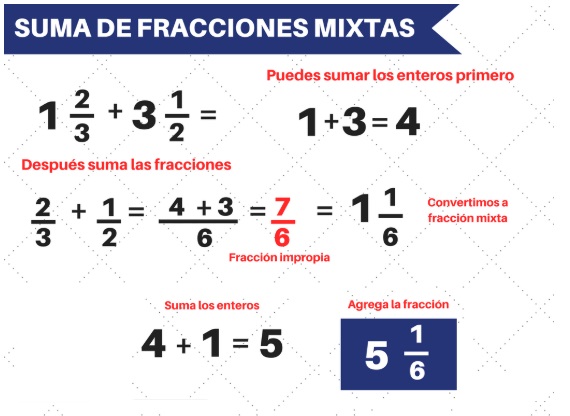
Suma de fracciones mixtas - 2daa forma:

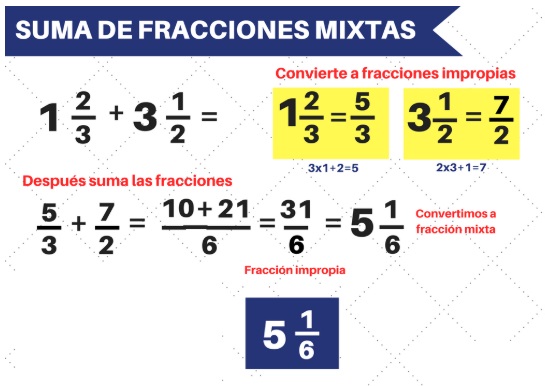
Si se te dificultó el tema, te invito a observar el siguiente video:

Actividad 4: (En línea)

a.  Suma de 2 fracciones con el mismo denominador: 

https://www.mathgames.com/skill/4.59-add-two-fractions

b.  Resta de 2 fracciones con el mismo denominador:  https://www.mathgames.com/skill/4.60-subtract-two-fractions

c. suma de 2 fracciones mixtas:  https://www.mathgames.com/skill/4.63-add-two-mixed-fractions

d.  Resta de 2 fracciones mixtas:  https://www.mathgames.com/skill/4.64-subtract-two-mixed-fractions

e. Suma de fracciones con diferente denominador (debes simplificar): https://www.mathgames.com/skill/5.68-add-fractions-with-unlike-denominatorshttps://www.mathgames.com/skill/5.68-add-fractions-with-unlike-denominators

f. Resta de fracciones con diferente denominador (debes simplificar): https://www.mathgames.com/skill/5.69-subtract-fractions-with-unlike-denominators 

B. MULTIPLICACIÓN Y DIVISIÓN

MULTIPLICACIÓN

Para multiplicar dos fracciones, simplemente multiplica los numeradores para obtener el numerador del producto y multiplica los denominadores para obtener el denominador del producto. 

Ejemplo:

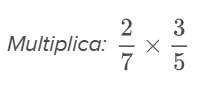
Multiplica los numeradores y los denominadores. 

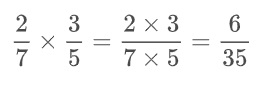
DIVISIÓN

Para dividir dos fracciones, primero debes encontrar el recíproco del divisor. Esto significa que debes dar vuelta la segunda fracción. Luego, multiplica los numeradores y multiplica los denominadores. 

Ejemplo:

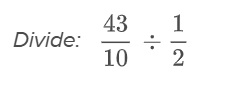
1ra forma:  invierte la segunda fracción y multiplica

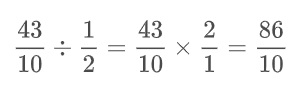
2da forma: multiplica en cruz 

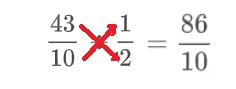
Finalmente, simplifica la fracción. 

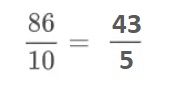
Actividad 5: (En línea)

a. Realiza las divisiones en el siguiente enlace a través del juego (Enséñale los resultados a tu docente):

https://wordwall.net/es/resource/4063528/multiplicaci%C3%B3n-y-divisi%C3%B3n-de-fracciones-6-b%C3%A1sico 

b. Realiza las multiplicaciones y divisiones en el siguiente enlace a través del juego (Enséñale los resultados a tu docente):

https://wordwall.net/es/resource/4491777/multiplicaci%C3%B3n-y-divisi%C3%B3n-de-fracciones 

c. En este ejercicio el docente utilizará una ruleta virtual y el primero que realice la operación en el cuaderno gana puntos extras:

https://wordwall.net/es/resource/14484526/multiplicaci%C3%B3n-y-divisi%C3%B3n-de-fracciones