Grado 11 Estadística

Periodo 3

Temas:

PROBABILIDAD

Concepto

Probabilidad, experimento, resultado, evento, espacio muestral

Enfoques de probabilidad

Subjetiva
Objetiva
Aletoriedad

Reglas

Adición
Complemento
Conjunta
Multiplicación
Condicional

Principios de conteo

Formula de multiplicación
Formula de permutación
Formula de combinación

PROBABILIDAD

Las probabilidades pertenecen a la rama de la matemática que estudia ciertos experimentos llamados aleatorios, es decir, regidos por el azar, en que se conocen todos los resultados posibles, pero no es posible tener certeza de cuál será en particular el resultado del experimento.

Por ejemplo, experimentos aleatorios cotidianos son:

1. El lanzamiento de una moneda

2. El lanzamiento de un dado

3. La extracción de una carta de un mazo de naipes.

ESPACIO MUESTRAL (𝛀): Se llama ESPACIO MUESTRAL (Ω) asociado a un experimento aleatorio, al conjunto de todos los posibles resultados de dicho experimento.

Ejemplo1. Al lanzar una moneda, el espacio muestral es (𝛀) = {cara, sello}, tiene dos elementos.

Ejemplo2. Al lanzar un dado de seis caras, el espacio muestral es (𝛀) = {1,2,3,4,5,6}, es decir tiene 6 elementos.

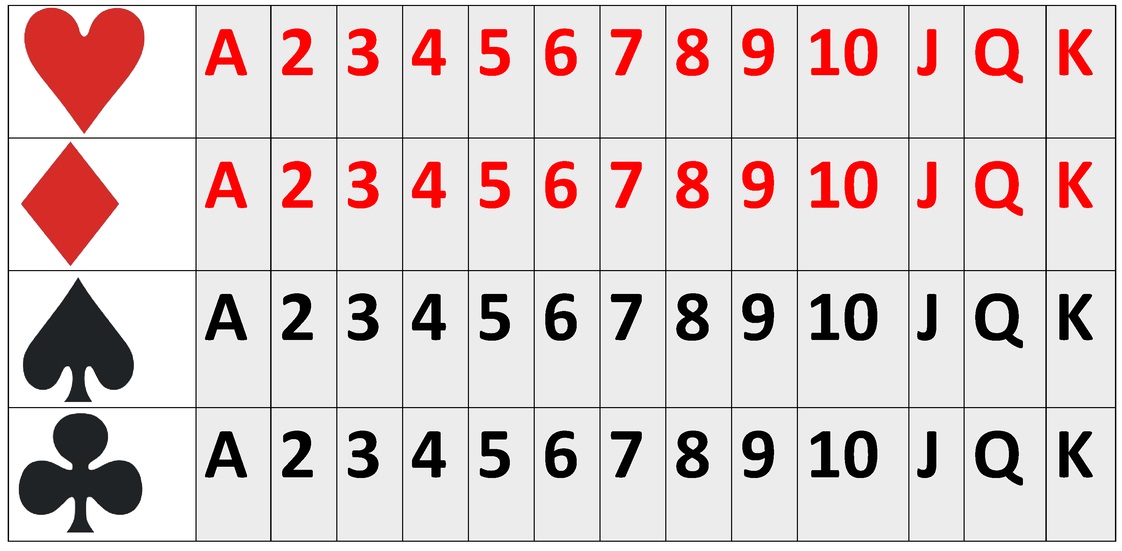
Ejemplo3. Se saca una carta de un mazo de poker, el espacio muestral es (𝛀) = {1,2,3,4,...,52}, tiene 52 elementos:

EVENTO O SUCESO: Se llama evento o suceso a todo subconjunto (parte de un conjunto) de un espacio muestral.

Ejemplo: en el espacio muestral (Ω) = {1,2,3,4,5,6} del lanzamiento de un dado, los siguientes son eventos: Obtener un número primo: A = {2,3,5}

Obtener un número primo y par: B = {2}

Obtener un número mayor o igual a 5: C = {5,6}

EJERCICIO1:

En los siguientes experimentos aleatorios, señale el espacio muestral y la cantidad de elementos de éste: a) Tirar dos monedas al mismo tiempo. No. de elementos = 4: Ω = { cara, sello, cara, sello}

b) Pinta que tendrá una carta escogida al azar de un naipe inglés (Averiguar sobre el naipe inglés).

No. de elementos = _______ Ω = { _____________ }

c) Pinta que tendrá una carta escogida al azar de un naipe español (Averigua sobre el naipe español).

No. de elementos = _______ Ω = { _____________ }

d) Si se lanza un dado y una moneda al mismo tiempo. Señale el espacio muestral

No. de elementos = _______ Ω = { _______________ }

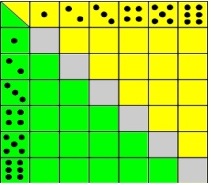
e) Se lanzan dos dados al mismo tiempo, señale los posibles resultados.

No. de elementos = _______ Ω = { _______________ }

f) Se lanzan tres monedas al mismo tiempo, señale los posibles resultados.

No. de elementos = _______ Ω = { _______________ }

REGLA DE LAPLACE

Si en un experimento aleatorio todos los resultados son equiprobables, es decir, la ocurrencia de uno es igualmente posible que la ocurrencia de cualquiera de los demás, entonces, la probabilidad de un evento A se define como:

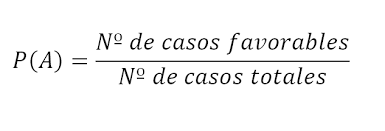
Ejemplo: Determinar la probabilidad de que al lanzar un dado salga el número 3. Tenemos sólo un caso favorable, que salga el tres; mientras que los casos posibles son seis, que corresponde a los números del dado. Por lo tanto:

A = Que salga el número 3 al lanzar un dado

Número de casos posibles: 6

Número de casos favorables: 1

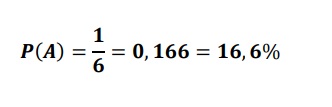
EJERCICIO2:

Calcule las siguientes probabilidades:

1) Sacar un cuatro al lanzar un dado.

2) Sacar un as de un mazo de naipe español.

3) Sacar una bolita roja de una caja que contiene 5 bolitas rojas, 18 azules y 7 negras.

4) En un equipo de fútbol están en la cancha 5 delanteros, 3 medios campistas, 2 defensas y el arquero. Se lastima uno de los jugadores, ¿cuál es la probabilidad de que sea un defensa el que se lesione?

5) De un mazo inglés (52 cartas), se puede tomar 1 carta, ¿cuál es la probabilidad que ésta sea una figura?

6) En una caja hay 12 esferas negra y 8 esferas verdes, ¿qué probabilidad hay de sacar una bola negra?

7) Hay 16 monedas de $100, 22 monedas de $50 y 12 monedas de $10. Al sacar una moneda, ¿cuál es la probabilidad de sacar una moneda de $100?

8) Al lanzar dos dados, ¿cuál es la probabilidad de:

a) Obtener 2 al sumar los números de sus lados

b) Obtener suma 12

Probabilidad objetiva, subjetiva y aleatoriedad

(Tomado de: https://es.linkedin.com/pulse/probabilidad-objetiva-subjetiva-y-aleatoriedad)

1. Posibilidad objetiva:

(También llamadas probabilidades frecuentistas o probabilidades clásicas)

Es una medida de la incertidumbre que se basa en la frecuencia histórica de un evento o en su relación con otros eventos similares, se basan en evidencia empírica

Un ejemplo puede ser la predicción de fallas en una red eléctrica. Imagina una empresa de distribución de energía eléctrica que opera una extensa red de transmisión y distribución. Con base en datos históricos de fallas, información sobre el estado de los equipos, análisis de desgaste y mantenimiento preventivo, es posible calcular objetivamente la probabilidad de fallas en diferentes componentes de la red, como transformadores, cables o postes. La empresa puede utilizar métodos estadísticos avanzados, como el análisis de confiabilidad de sistemas, para identificar patrones y estimar la probabilidad de fallas en determinados intervalos de tiempo. Este enfoque objetivo permite una planificación adecuada del mantenimiento, asignación de recursos y reducción de los riesgos operativos.

Métodos:

La probabilidad objetiva se puede calcular mediante diferentes métodos y fórmulas dependiendo del tipo de datos y de la pregunta que queramos responder. Algunos de los métodos y fórmulas más comunes son:

- Frecuencia relativa: Este método utiliza la proporción de veces que ocurre un evento en una gran cantidad de ensayos u observaciones.

Por ejemplo, si lanzamos una moneda justa 100 veces y observamos 52 caras y 48 cruces, la frecuencia relativa de caras es 52/100 = 0,52, lo que significa que la probabilidad objetiva de obtener cara en un lanzamiento es 0,52 (Ver regla de laplace).

- Probabilidad clásica: este método utiliza la relación entre resultados favorables y resultados posibles cuando todos los resultados son igualmente probables.

Por ejemplo, si lanzamos una vez un dado justo de seis caras, la probabilidad clásica de obtener un 4 es 1/6, porque sólo hay un resultado favorable (4) de seis resultados posibles (1, 2, 3, 4, 5, 6).

- Probabilidad binomial: Esta fórmula calcula la probabilidad de obtener un número específico de éxitos en un número fijo de ensayos independientes con dos resultados posibles (éxito o fracaso).

Por ejemplo, si lanzamos una moneda tres veces, la probabilidad binomial (se ve en 4to periodo) de obtener exactamente dos caras es (3 eligen 2) (0,5)^2 (0,5)^1 = 0,375, donde (3 eligen 2) es el número de formas de disponer dos caras y una cruz en tres lanzamientos.

- Probabilidad normal: esta fórmula calcula la probabilidad de obtener un valor dentro de un rango determinado en una distribución continua, simétrica y con forma de campana.

Por ejemplo, si medimos la altura de 1000 hombres adultos y encontramos que siguen una distribución normal con media de 1,75 cm y desviación estándar de 10 cm, la probabilidad normal (se ve en 4to periodo) de obtener una altura entre 1,65 cm y 1,85 cm es 0,6827, lo que significa que aproximadamente El 68% de los varones tiene alturas en este rango.

- Otras distribuciones de probabilidad: existen muchos otros tipos de distribuciones de probabilidad que se pueden usar para modelar diferentes tipos de datos y fenómenos, como Poisson, exponencial, chi-cuadrado, distribución t, etc. La distribución tiene su propia fórmula y parámetros que determinan su forma y características.

2. Probabilidad Subjetiva

Probabilidad como grado de creencia individual. establece que, en cualquier situación de incertidumbre, las distintas alternativas deben considerarse equiprobables si no hay razón para esperar una más que otra

Un ejemplo de probabilidad subjetiva es la evaluación de riesgos geopolíticos en una organización global. Considera una empresa multinacional que opera en varios países con entornos políticos y sociales complejos y en constante cambio. En este caso, calcular probabilidades objetivas basadas en datos históricos puede ser desafiante debido a la falta de patrones claros o a la falta de información confiable. En cambio, la organización debe recurrir a la evaluación subjetiva de los riesgos geopolíticos, teniendo en cuenta análisis de expertos en política internacional, información de agencias de inteligencia, análisis de escenarios y percepciones regionales (Es decir los datos no son propios de la empresa, son datos externos o que están influenciadas por creencias u opiniones personales ). Este enfoque subjetivo permite que la empresa tome decisiones estratégicas con más confianza, como ingresar a nuevos mercados o asignar recursos en regiones con mayor o menor estabilidad política.

* Estos ejemplos demuestran cómo la gestión de riesgos puede abordarse de maneras distintas, según la disponibilidad de datos y la naturaleza de los eventos analizados.

3. Aleatoriedad

Cuando lazamos un dado no sabemos qué número va a salir; sin embargo, si lanzamos una piedra al aire estamos seguros de que caerá al suelo. Es decir, en algunos experimentos podemos saber lo que va a ocurrir y en otros no.

A los experimentos en los cuales no sabemos lo que va a ocurrir se les llama experimentos aleatorios.
A los otros, aquellos en los que sí podemos decir lo que va a ocurrir, se les llama experimentos deterministas.

Solo para hacer más comprensible los dos ejemplos iniciales, consideramos necesario aclarar cuáles son las premisas mínimas para que los experimentos se consideren aleatorios:

Repetibilidad: El experimento debe ser repetible, es decir, es posible realizar el mismo experimento varias veces bajo condiciones similares;
Independencia: Los resultados de un experimento no deben influir en los resultados de otros experimentos. Cada experimento debe ser realizado de forma independiente;
Equi-probabilidad: Cada resultado posible del experimento debe tener la misma probabilidad de ocurrir. Esto significa que todos los resultados tienen las mismas posibilidades de obtenerse;
Resultados mutuamente excluyentes: Los resultados posibles del experimento deben ser mutuamente excluyentes, lo que significa que solo un resultado puede ocurrir en cada intento del experimento;
Determinismo: Las premisas de aleatoriedad deben aplicarse antes de que ocurra el experimento, es decir, no debe haber ningún factor determinista conocido que influya en el resultado del experimento.

* Es importante destacar que no todos los eventos de la vida real cumplen con estas premisas, lo que hace que el cálculo objetivo de frecuencias sea inviable en muchos casos. En estas situaciones, el enfoque subjetivo puede ser más apropiado para evaluar y gestionar riesgos

REGLAS

1. SUMA O ADICIÓN DE PROBABILIDADES

Establece que si tenemos un evento A y un evento B, la probabilidad de que ocurra el evento A o el evento B se calcula de la siguiente manera:

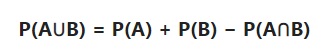
Donde:

P(A) : probabilidad de que ocurra el evento A.
P(B) : probabilidad de que ocurra el evento B.
P(A⋃B) : probabilidad de que ocurra el evento A o el evento B.
P(A⋂B) : probabilidad de que ocurra el evento A y el evento B a la vez.

¿Y si los eventos son mutuamente excluyentes?

Dos eventos A y B son mutuamente excluyentes si no pueden ocurrir al mismo tiempo, es decir, si no tienen elementos comunes. Por ejemplo, sacar una carta al azar de una bajara, y obtener un 5 y un 7, son eventos mutuamente excluyentes, ya que no hay ninguna carta que tenga un 5 y un 7 al mismo tiempo. Entonces P(A⋂B) = 0 , por lo tanto, partiendo de la misma fórmula, obtendríamos la siguiente expresión:

P(A⋃B) = P(A) + P(B) − P(A⋂B)

P(A⋃B) = P(A) + P(B) − 0

P(A⋃B) = P(A) +P(B)

Ejemplo 1:

La probabilidad de que un día cualquiera, Carlos almuerce pollo frito es de 0,4. La probabilidad de que almuerce hamburguesa es de 0,3; mientras que la probabilidad de que almuerce pollo frito y hamburguesa el mismo día es de 0,1. Calcula la probabilidad de que un día cualquiera, Carlos almuerce pollo frito o hamburguesa.

Solución:

Definimos nuestras probabilidades:

Probabilidad de que Carlos almuerce pollo frito: P(A) = 0,4.
Probabilidad de que Carlos almuerce hamburguesa: P(B) = 0,3.
Probabilidad de que Carlos almuerce pollo frito y hamburguesa el mismo día: P(A⋂B) = 0,1.
Probabilidad de que Carlos almuerce pollo frito o hamburguesa:
P(A⋃B) = ?

Ahora, aplicamos nuestra fórmula:

P(A⋃B) = P(A) + P(B) − P(A⋂B)

P(A⋃B) = 0,4 + 0,3 − 0,1

P(A⋃B) = 0,6

Ejemplo 2:

La probabilidad de que al tirar un dado, salga 1, es de 1/6. La probabilidad de que salga 3, es de 1/6. Calcular la probabilidad de que al tirar un dado, salga 1 o 3.

Solución:

Definimos nuestros eventos:

Probabilidad de que salga 1: P(A) = 1/6.
Probabilidad de que salga 3: P(B) = 1/6.
Probabilidad de que salga 1 y 3 al mismo tiempo P(A⋂B) = 0. Este valor es cero, dado que son eventos mutuamente excluyentes. Si sale 1, ya no puede salir 3.
Probabilidad de que salga 1 o 3: P(A⋃B) = ?

Ahora, aplicamos nuestra fórmula:

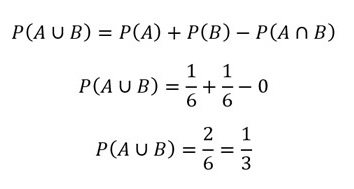
Si no entendiste el tema, te invito a observar el siguiente video:

EJERCICIO3:

1. Hay 60 alumnos en un salón, de los cuales a 37 les gusta el fútbol y a 38 les gusta el básquet.

Además, a todos los alumnos les gusta al menos uno de esos dos deportes. Si se selecciona un

alumno al azar,

a) ¿cuál es la probabilidad de que le guste solo el fútbol?

b) ¿y solo el básquet?

Respuestas: a) 0,3637 b) 0,3833

2. Una empresa minera compra un terreno en Perú. Los estudios determinaron las siguientes

probabilidades previas:

a. P(encontrar oro de buena calidad)=0.50

b. P(encontrar oro de mala calidad)=0.30

c. P(no encontrar oro)=0.20

Calcular la probabilidad de encontrar oro en dicho terreno.

Respuesta: 0,80

3. Sea A el suceso de sacar un 3 en una baraja de 52 cartas y B el suceso sacar un 5 de corazones. Calcular la probabilidad de sacar un 3 o un 5 de corazones en una sola extracción.

Rpta: 5/52 = 0,0961

4. En un salón con 7 hombres y 8 mujeres, se desea formar un comité de 2 personas. ¿Cuál es la probabilidad de que esté formado por un hombre y una mujer?

Rpta: 0,5333

5. La probabilidad de que Julio salga con Carla es 0,75, y la probabilidad de que salga con Marisol es de 0,50. Si la probabilidad de que salga con Carla o Marisol es 0,85; calcular la probabilidad de que salga con ambas a la vez.

Rpta: 0,40.

6. Un chef observó que el 65 % de todos sus clientes consume mayonesa, el 70 % consume kétchup y el 80 % consume mayonesa o kétchup.

¿Cuál es la probabilidad de que un cliente consuma las dos salsas al mismo tiempo?

Rpta: 0,55 o 55 %.

7. En un grupo de estudiantes del colegio ABC se sabe que el 30% inglés, el 65% habla francés, y el 12% habla los dos idiomas. Si se selecciona un alumno al azar,

a) ¿cuál es la probabilidad de que hable inglés o francés?

b) ¿cuál es la probabilidad de que no hable ni inglés ni francés?

Rpta: a) 0,83 b) 0,17.

8. Sabiendo que P(A) = 0,80; P(B) = 0,10; y además, P(A∩B)=0,08; determinar si son eventos independientes o no.

Rpta: si son independientes.

2. PROPABILIDAD DE COMPLEMENTO

La regla de complementación o regla del complemento nos dice que si tenemos un evento A, y su suceso contrario o complementario Ā, entonces, se cumple que: P(Ā) = 1 – P(A)

También podemos expresarlo como: «la probabilidad de que no ocurra A, es 1 menos la probabilidad de que ocurra A».

Ejemplo 1

La probabilidad de que el FC Barcelona gane un partido jugando de local, es de 0,83. Calcular la probabilidad de que empate o pierda un partido jugando de local.

Suceso A: ganar el próximo partido de local. Del enunciado, conocemos el valor de P(A)

P(A) = 0,83

Suceso Ā : no ganar el próximo partido de local, es decir, que empate o pierda. Si calculamos P(Ā)

P(Ā) = 1 – P(A)

P( Ā ) = 1 – 0,83 = 0,17

La probabilidad de que el Barcelona empate o pierda en su próximo partido de local es de 0,17.

Ejemplo 2:

Calcular la probabilidad de no obtener un 1 al lanzar un dado al aire.

Suceso A: obtener un 1 al lanzar un dado al aire. A={ 1 }. Si calculamos P(A):

Suceso Ā : no obtener un 1 al lanzar un dado al aire, es decir, obtener un 2, 3, 4, 5 o 6. Ā = {2, 3, 4, 5, 6}. Si calculamos P(Ā):

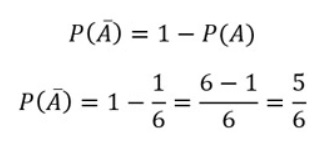
Si no entendiste el tema te invito a observar el siguiente video:

EJERCICIO4:

1. Hay 60 alumnos en un salón, de los cuales a 37 les gusta el fútbol y a 38 les gusta el básquet.

Además, a todos los alumnos les gusta al menos uno de esos dos deportes. Si se selecciona un

alumno al azar,

a) ¿cuál es la probabilidad de que NO le guste solo el fútbol?

b) ¿y NO le guste solo el básquet?

Respuestas: a) 0,3637 b) 0,3833.

2. Imagine que es gerente de un centro de llamadas y desea evaluar la tasa de éxito de sus empleados a la hora de resolver los problemas de los clientes por teléfono. Si sabe que el 70% de las llamadas se resuelven exitosamente, puede usar la regla del complemento para determinar el porcentaje de llamadas que no se resuelven exitosamente.

Respuestas: a) 30%

3. Suponga que trabaja en control de calidad para una empresa de fabricación y desea analizar la tasa de defectos de una línea de productos en particular. Si sabes que sólo el 5% de los productos tienen defectos, aplica la regla del complemento para saber qué porcentaje de productos no tienen ningún defecto.

2. PROBABILIDAD CONJUNTA

Es la probabilidad de que dos o más eventos ocurran simultáneamente, se suele denotar como P(A y B), donde A y B son dos eventos.

A continuación, se presentan tres ejemplos de probabilidad conjunta:

Lanzamiento de dos dados: Se lanzan dos dados y se quiere conocer la probabilidad de que ambos den un número par. Los eventos A y B se definen como "el primer dado da un número par" y "el segundo dado da un número par", respectivamente. La probabilidad conjunta de que ambos den un número par es:

P(A y B) = P(A) * P(B) = (1/2) * (1/2) = 1/4

Selección de cartas: Se tiene un mazo de cartas y se extraen dos cartas sin reemplazo. Se quiere conocer la probabilidad de que ambas cartas sean ases. Los eventos A y B se definen como "la primera carta es un as" y "la segunda carta es un as", respectivamente. La probabilidad conjunta de que ambas sean ases es:

P(A y B) = P(A) * P(B|A) = (4/52) * (3/51) = 1/221

Donde P(A) es la probabilidad de que la primera carta sea un as (4 ases en un mazo de 52 cartas) y P(B|A) es la probabilidad de que la segunda carta sea un as dado que la primera es un as (hay 3 ases en un mazo de 51 cartas después de haber sacado uno).

Fallas en una planta: Se tiene una planta que produce piezas de un producto y se sabe que la probabilidad de que una pieza tenga una falla es del 5%. Se quiere conocer la probabilidad de que en una muestra de 10 piezas haya exactamente 2 piezas con fallas. Los eventos A y B se definen como "una pieza tiene una falla" y "hay exactamente 2 piezas con fallas en una muestra de 10 piezas", respectivamente. La probabilidad conjunta de que ocurra el evento B es:

P(A y B) = P(B|A) * P(A) * P(B|no A) * P(no A)^8

Donde P(B|A) es la probabilidad de que haya 2 piezas con fallas dada que la primera pieza tiene una falla (P(B|A) = C(9,1)0.050.95^8), P(A) es la probabilidad de que la primera pieza tenga una falla (0.05), P(B|no A) es la probabilidad de que haya 2 piezas con fallas dada que la primera pieza no tiene una falla (P(B|no A) = C(9,2)0.05^20.95^7) y P(no A)^8 es la probabilidad de que las otras 8 piezas no tengan fallas (0.95^8). La probabilidad conjunta es:

P(A y B) = (C(9,1)0.050.95^8) * (0.05) * (C(9,2)0.05^20.95^7) * (0.95)^8 ≈ 0.0721

Donde C(n,k) es el coeficiente binomial que representa el número