Grado 11 - Cálculo
Periodo 3


DBA 7. Usa propiedades y modelos funcionales para analizar situaciones y para establecer relaciones funcionales
entre variables que permiten estudiar
la variación en situaciones intra escolares y extraescolares

ESTÁNDAR BÁSICO DE COMPETENCIA: Modela situaciones de variación con funciones polinómicas.
INDICADOR DE DESEMPEÑO: Interpretar el concepto de límite de una función
gráficamente y determinar su valor utilizando las diferentes funciones de variable
real.
TEMAS:
1. Limites - 2. Definición formal de limite - 3. Limites laterales - 4. Limites racionales -
5. Límites de funciones indeterminadas - 6. Límites de funciones trigonométricas
7. Continuidad / Funciones continuas / Continuidad de una función en un punto
8. Discontinuidad

Secuencia numérica: Una secuencia o sucesión numérica es una lista de números. El orden importa:
Por ejemplo: la secuencia 1, 2, 3 es distinta de la secuencia 2, 3, 1. Una secuencia es infinita si nunca termina.
Por ejemplo: la secuencia de los números pares positivos, en orden, es infinita: 2, 4, 6, 8, 10, 12, ... Podemos describir una secuencia usando una expresión general para su n-ésimo término.
Por ejemplo: si decimos que a(n) = 3n+1, y comenzamos en n = 1, entonces estamos hablando de esta secuencia: 4, 7, 10, 13, 16. Esta es una secuencia aritmética, en donde la diferencia entre un término y el anterior es constante.
También podemos representar una secuencia gráficamente como una función: el eje horizontal se usa
para n = 1, 2, 3,... y el eje vertical para los valores a(n) de la secuencia.
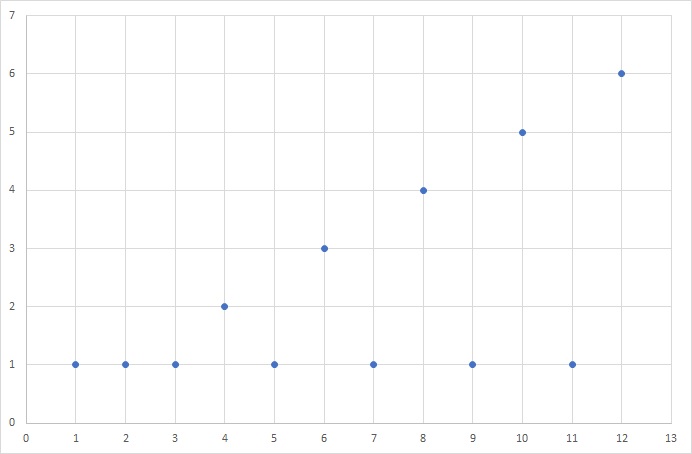
Por ejemplo: la secuencia infinita 1, 1, 1, 2, 1, 3, 1, 4, 1, 5, 1, 6, … se representa gráficamente como se ve en la gráfica de abajo. Y en fórmulas, se describe así:
a(n) = 1, si n es impar
a(n) = n/2, si n es par.
Si los numeros son n=1,2,3,4,5,... la secuencia quedaría de la siguiente manera:
a(n) = 1, 1, 1, 2, 1, 3, 1, 4, 1, 5,......... y su gráfica quedaría:
Una secuencia (a(n)) es creciente si se
tiene que cada término es mayor o
igual que el anterior. Es decir, para n
≥ 1, a(n+1) ≥ a(n).
Ejercicio 1:
1. Dibuja en el plano cada secuencia infinita:
a) 2, 2, 3, 3, 4, 4, 5, 5, 6, 6, …
b) 5, 5,2 , 5,22 , 5,222 , 5,222, …
c) La secuencia b dada por b(n) = (−1) 𝑛 .
2. Encuentra una fórmula (o varias, por casos) para cada secuencia:
a) −1, 4, 11, 20, 31, 40, 59, 76, 95, …
b) 1, 6, −1, 7, −1, 8, 1, 9, −1, 10, 1, 11, ...
1. LÍMITES
El límite de una función es un concepto fundamental del análisis matemático aplicado a las funciones.
A veces algo no se puede calcular directamente... ¡pero puedes saber cuál debe ser el resultado si te vas
acercando más y más! A esto lo llamamos el límite de una función.
EJEMPLO 1:
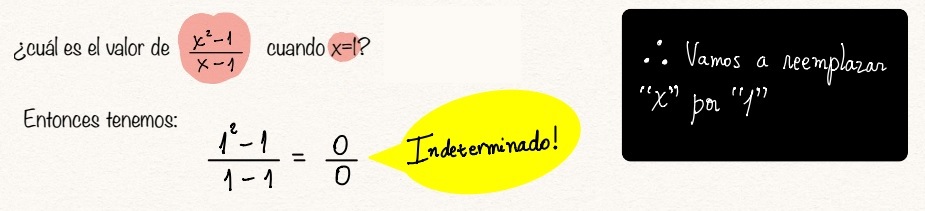
Una técnica para encontrar el verdadero valor de este ejemplo es acercándose al 1
por "valores cercanos": Lo veremos en la siguiente tabla:

A esto nos referimos cuando hablamos de límite. Y se simboliza de la
siguiente forma:
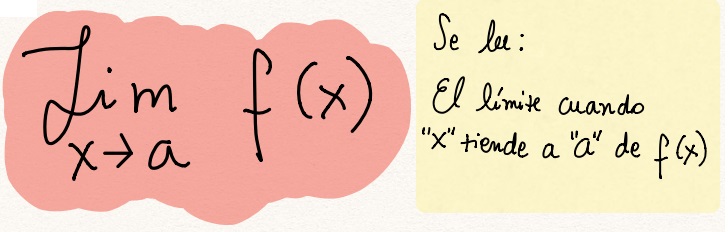
Para el ejemplo que estamos haciendo, la forma matemática de denotarlo sería:
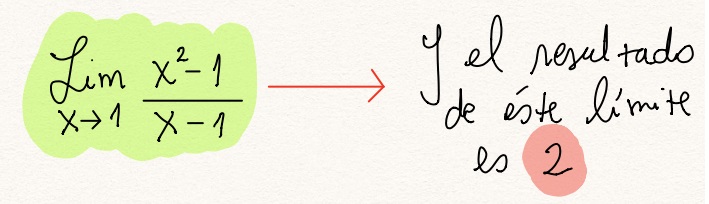
Vimos la forma tabular de calcular un límite, pero la manera más
común de hacerlo es de forma algebraica. Y sería la siguiente:

En la mayoría de las ocasiones para obtener el resultado de un límite,
basta sólo con reemplazar la "X" al valor a cual tiende.
Tal como en el siguiente ejemplo:
EJEMPLO 2:

Pero hay otras veces como en el primer ejemplo, donde al evaluar
el límite este se indefine, por lo que en estas ocasiones se debe
realizar un procedimiento algebraico (factorizar, simplificar,
racionalizar, etc.).
Para luego evaluar y encontrar el valor del límite.
EJEMPLO 3:
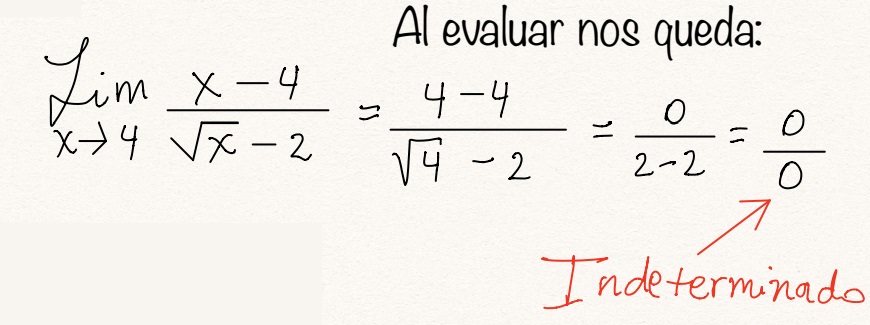
En este caso lo más
apropiado es racionalizar:
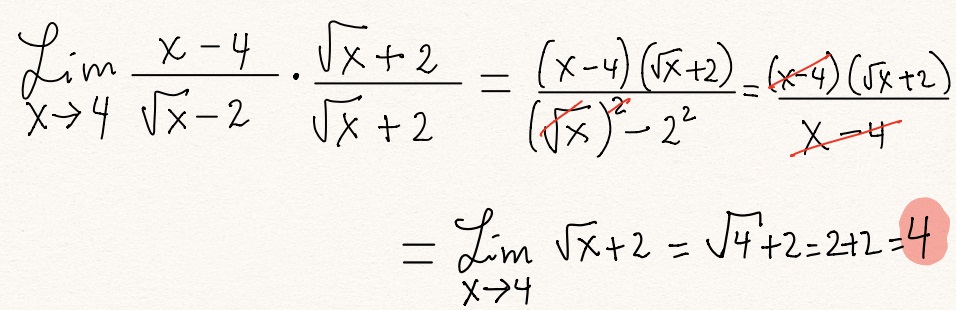
Para entender un poco más el concepto de límite te invito a observar los siguientes videos:
Ejercicio 2:
Desarrolla los siguientes problemas:
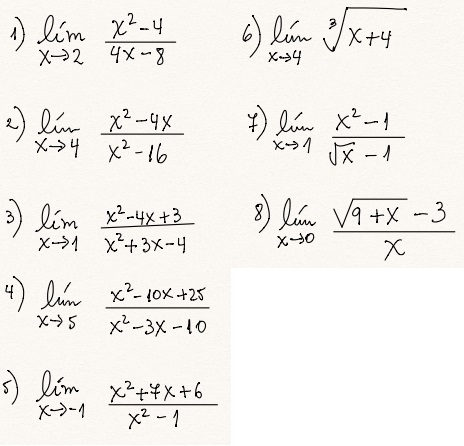
LÍMITE LATERAL
El concepto de límite lateral es el mismo que el de límite, pero considerando que x se aproxima al punto a por su derecha o por su izquierda.
EJEMPLO 1:
Consideremos la función f(x)=1/x y que queremos calcular su límite en 0, es decir,
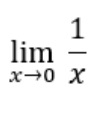
Cuando x toma valores cercanos a 0 por su derecha, f(x) toma valores positivos grandes:
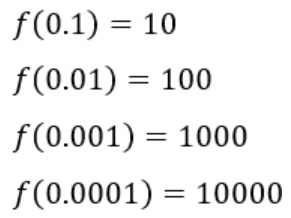
Deducimos que el límite de f(x) cuando x tiende a 0 por la derecha es infinito positivo:
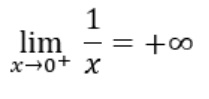
Sin embargo, si x se aproxima por la izquierda de 0, f(x) toma valores muy pequeños:
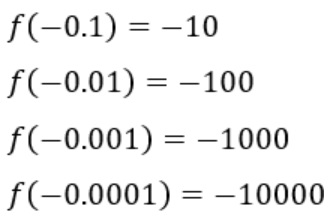
Por tanto, el límite de f(x) cuando x tiende a 0 por la izquierda es infinito negativo:
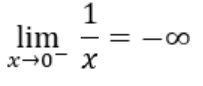
Has un recorrido de los puntos de la función 1/x en el siguiente enlace:
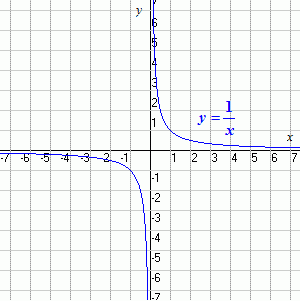
Nota: cuando buscas el límite por la derecha le colocas un + y si es por la izquierda un -
Ejemplo:
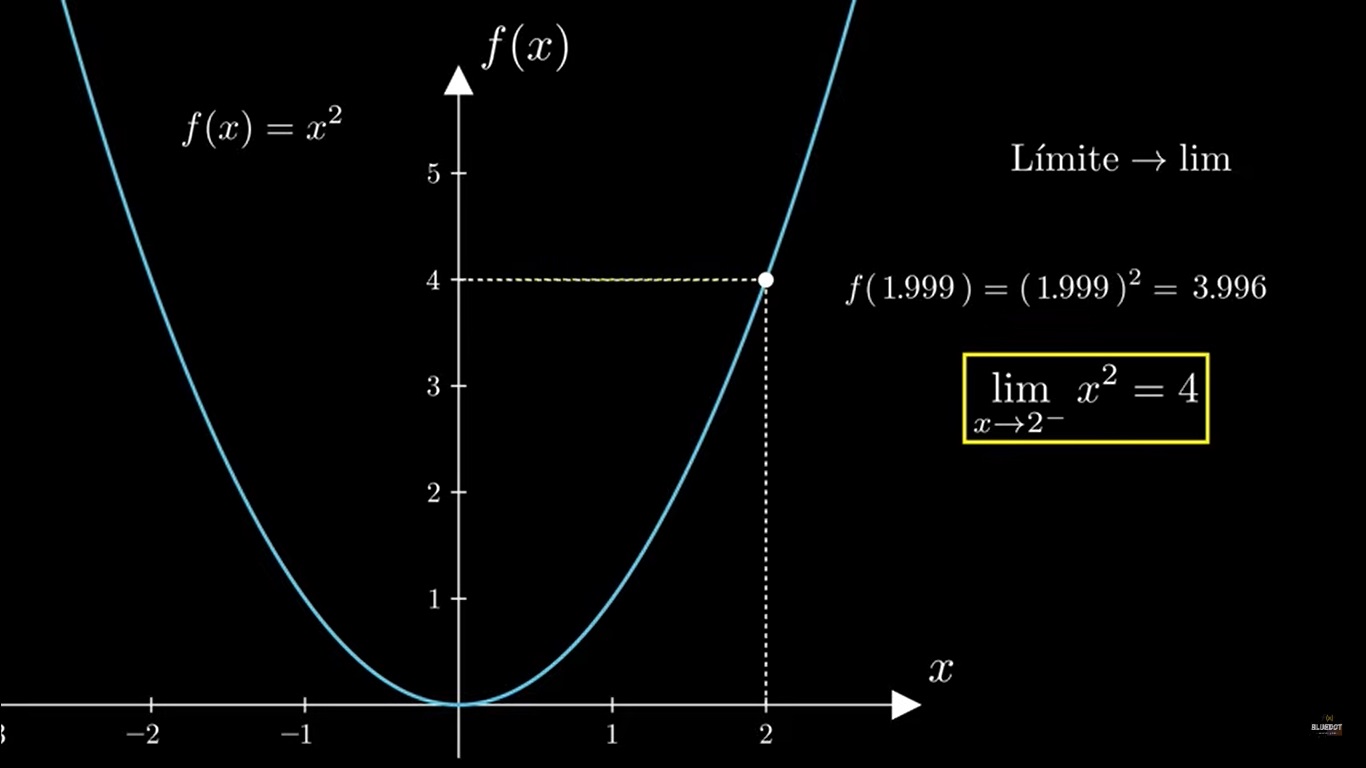
EJEMPLO 2:
En las funciones racionales (fracciones de polinomios), los puntos que anulan al denominador son puntos donde, generalmente, los límites laterales no coinciden. Veamos lo siguiente:
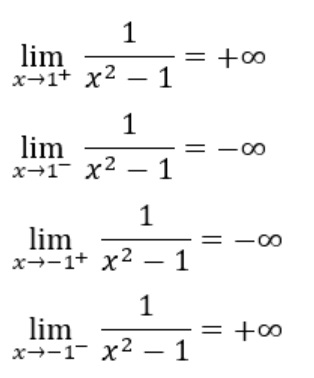
Gráfica:
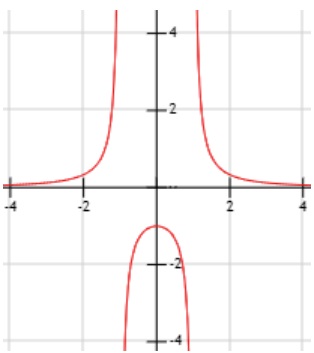
EJEMPLO 3:
En las funciones definidas a trozos, es habitual que no coincidan los límites laterales en los puntos donde cambia la definición.
Por ejemplo, sea la función
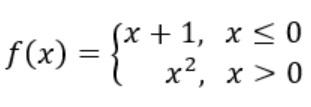
Los límites laterales en 0 son
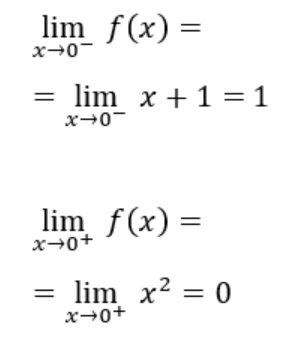
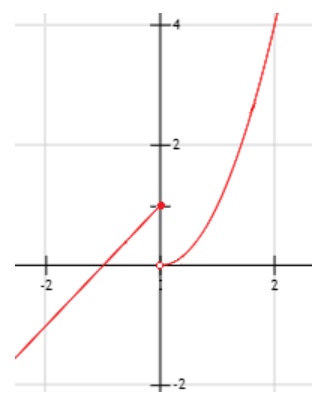
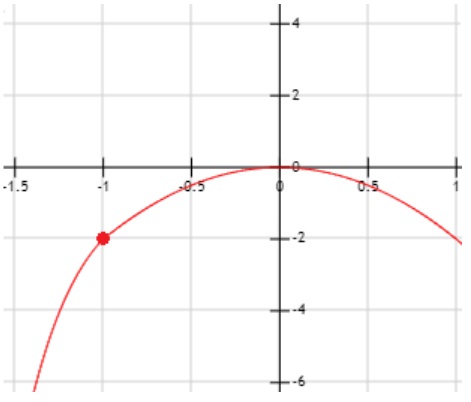
Su gráfica es la siguiente:
Ejercicio 3:
1. Calcular los siguientes límites laterales:
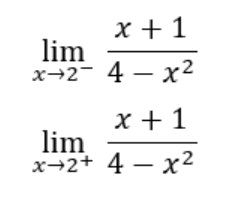
Gráfica:
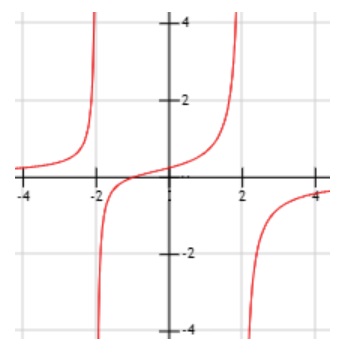
2. Calcular los siguientes límites laterales:
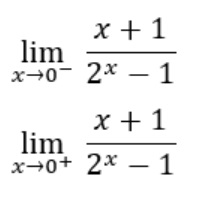
Gráfica:
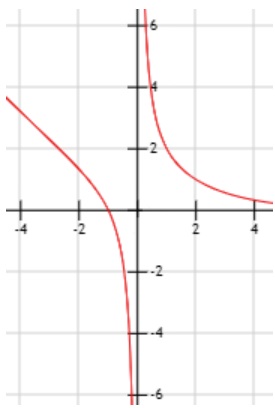
3. Calcular el siguiente límite:
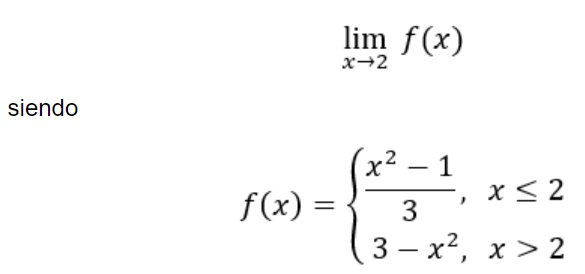
Gráfica:
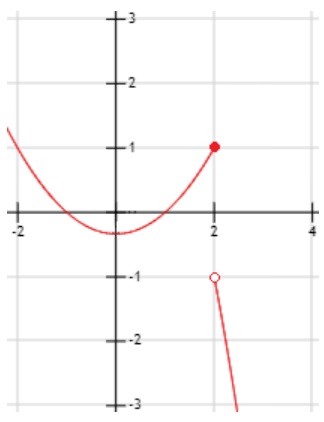
4. Calcular el siguiente límite:
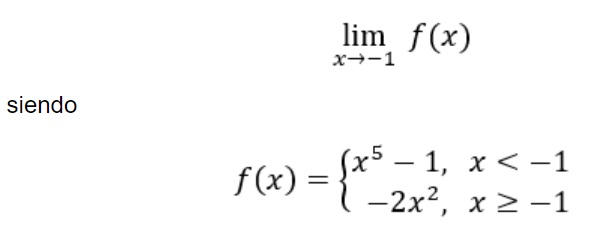
Gráfica:
LÍMITES DE FUNCIONES RACIONALES
Una función racional es una función del tipo:
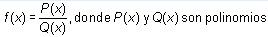
En el estudio de los límites de funciones racionales, debemos tener cuidado con las indeterminaciones que se nos presenten y tener conocimiento de álgebra, como por ejemplo, la factorización, potenciación, entre otras.
No existe una regla para resolver un límite, sin embargo, lo primero que haremos al enfrentar un problema será evaluarlo, luego buscar la forma de simplificarlo y volverlo a evaluar con el fin de obtener su valor final. Veamos algunos ejemplos:
EJEMPLO 1:
Calcular el valor del siguiente límite
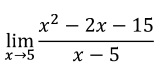
Primero lo evaluamos:
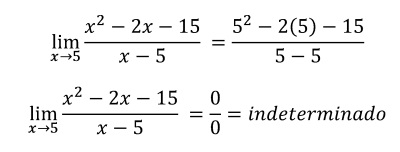
Factorizamos el numerador de la expresión:
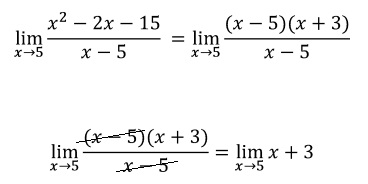
Simplificada la expresión volvemos a evaluar el límite:
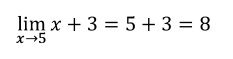
Entonces:
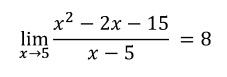
EJEMPLO 2: Calcular el valor del siguiente límite:
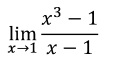
Primero lo evaluamos:
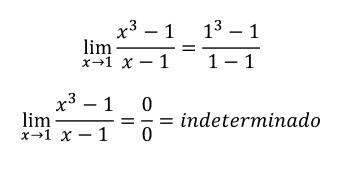
Luego factorizamos el numerador de la expresión:
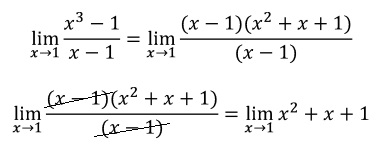
Como hemos simplificado la expresión, evaluamos el límite:
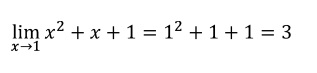
Entonces:
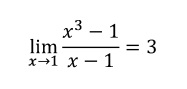
EJEMPLO 3: Calcular el valor del siguiente límite
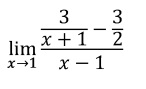
Primero lo evaluamos
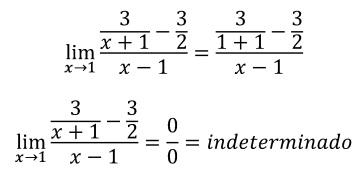
Restamos el numerador de la expresión:
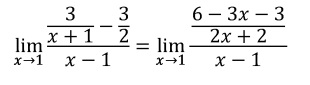
Dividimos las dos fracciones con la ley de la oreja:
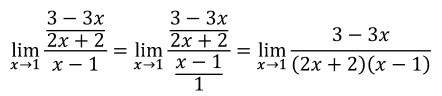
Sacamos factor común 3 del numerador:
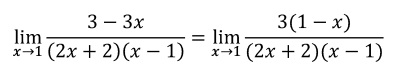
Sacamos factor común del signo en el numerador:
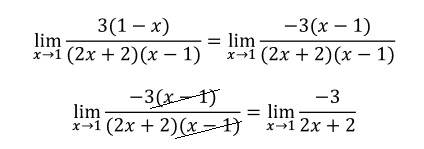
Volvemos a evaluar el límite:
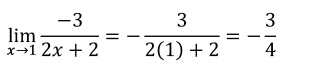
EJERCICIO 4: Desarrollar los siguientes límites en el cuaderno y presentarlo al docente:
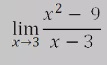
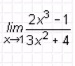
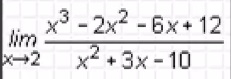
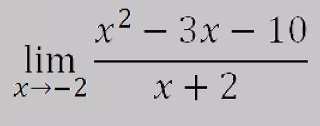
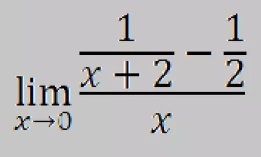
LÍMITES DE FUNCIONES INDETERMINADAS
En algunas ocasiones se presenta el cálculo de límites de cocientes, diferencias y productos de funciones en los que al reemplazar la variable por el valor al cual tiende se generan indeterminaciones del tipo:

entre otras El resultado de estos límites no puede anticiparse y el mismo puede ser 0, ∞ ó un número finito diferente de cero, o bien puede no existir. Para resolverlos, se realizan procedimientos algebraicos adecuados que permitan salvar la indeterminación.
Antes de iniciar con las indeterminaciones hay que analizar algunos cocientes que no lo son como:
Si K=1 y a medida que el denominador se parece más a cero, la relación aumenta. tendremos:
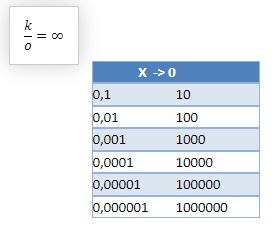
Caso contrario ocurre a continuación, a medida que aumenta el denominador la relación tiende a cero.
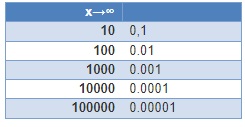
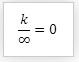
En un ejemplo práctico mientras más personas comparten una misma pizza menos comen cada una.
Este tipo de relaciones no son indeterminadas mientras que 0/0 e ∞/∞ si lo son, estas no se los puede determinar el valor porque en el caso de infinito son números grandes pero no se puede establecer cuanto
1.- Límites indeterminados 0/0
A.- Factorización
1.- Cuando el límite indeterminado es 0/0 y la tendencia es a cero, se realiza un factor común, como se muestra en el siguiente ejemplo:
Sea el siguiente límite

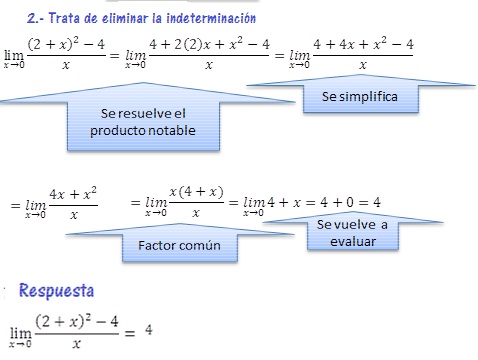
O QUE HAY QUE SABER PARA RESOLVER LÍMITES INDETERMINADOS
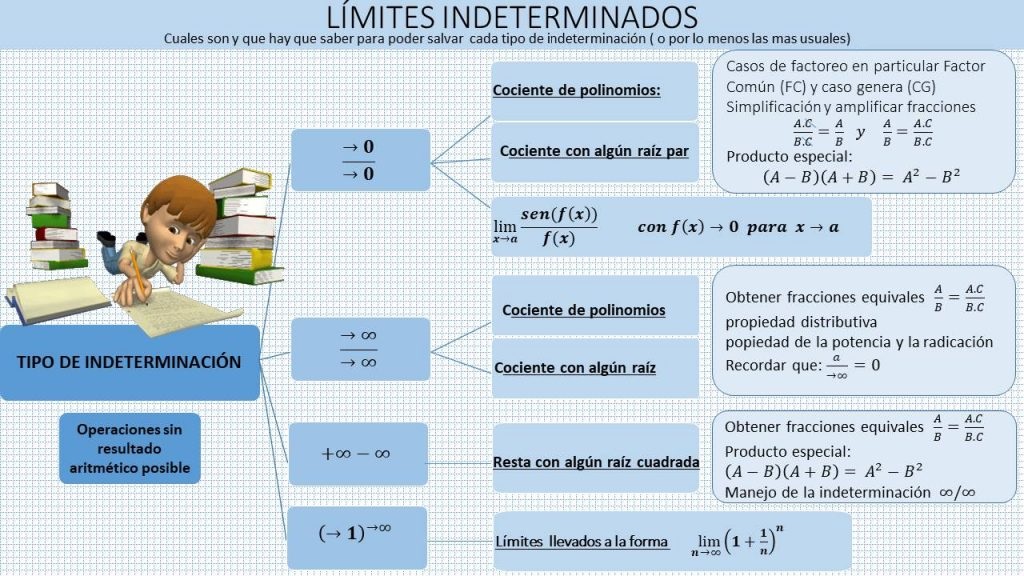
1. INDETERMINACIÓN: CERO/CERO
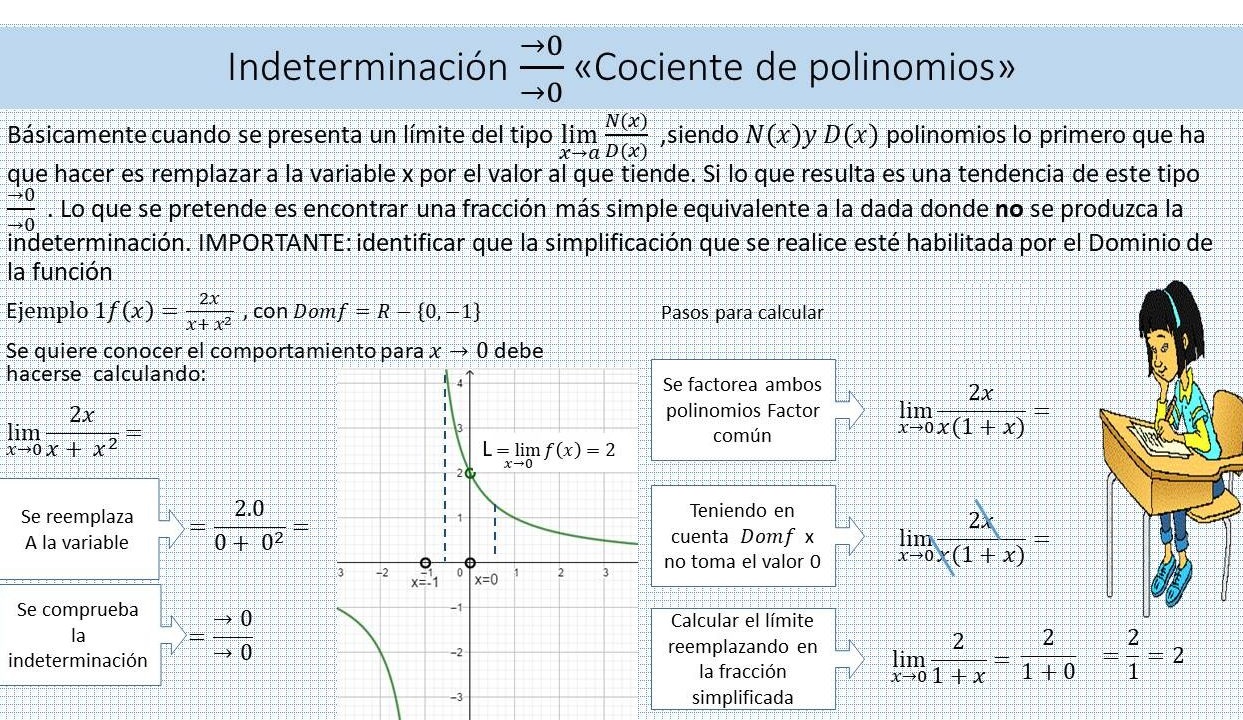
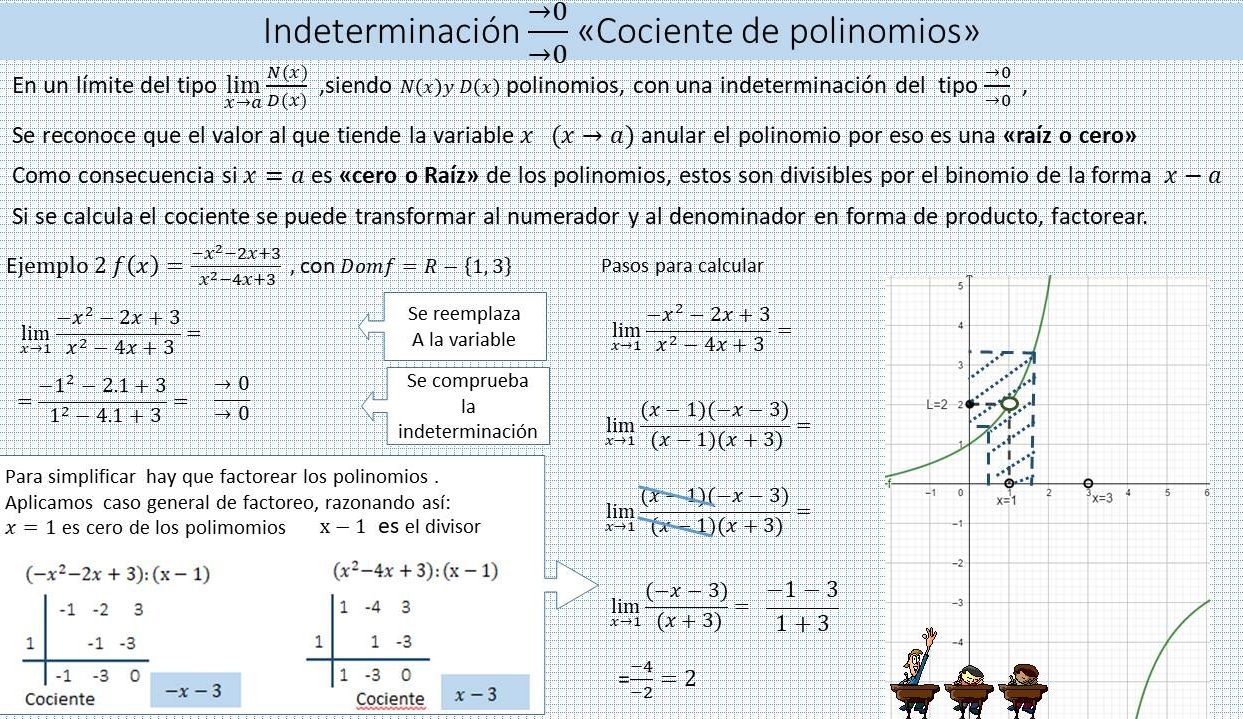
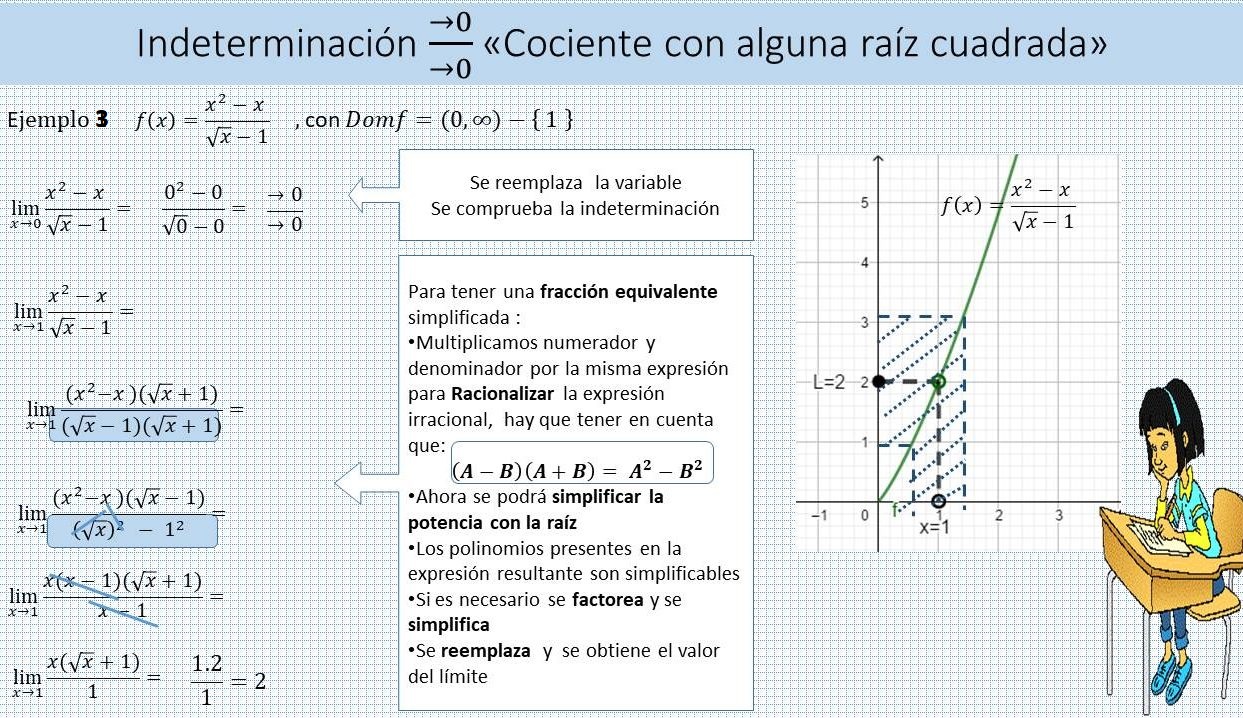
2. INDETERMINACIÓN: INFINITO /INFINITO
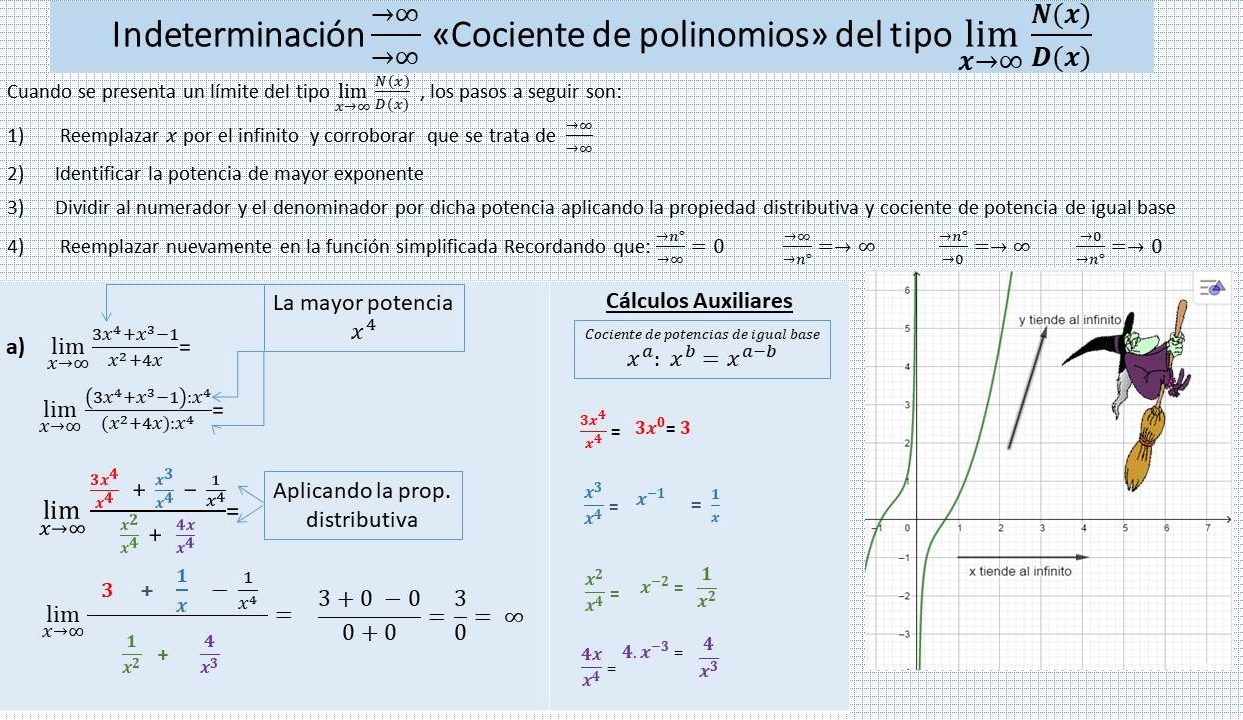


EJERCICIO 5: Resuelve los siguientes límites indeterminados:
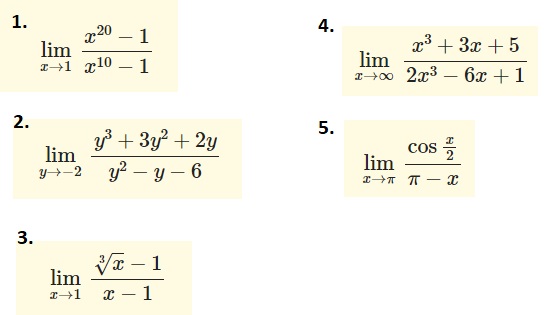
6. Límites de funciones trigonométricas
De la misma manera en que se puede calcular por sustitución directa los límites de muchas funciones algebraicas, también las funciones trigonométricas fundamentales cuentan con esa propiedad, como se enuncia en el siguiente teorema.
Teorema: Límites de funciones trigonométricas
Dado θ un número real en el dominio de una función trigonométrica dada:
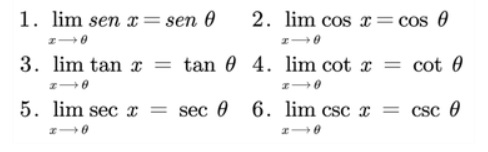
Además, dado un valor α, se cumple que:
Teorema 1
Si α es la medida de un ángulo dada en radianes, entonces podemos afirmar que:
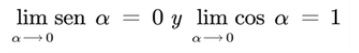
Es importante recordar que la medida en radianes de un ángulo se define como:
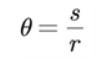
Donde s es la longitud del arco que subtiende el ángulo, sobre una circunferencia de radio r, cuyo centro coincide con el vértice del ángulo.
Teorema 2. Dos límites trigonométricos especiales
Nótese en estos 2 ejemplos los cuales sus límites no pueden resolverse por ninguno de los métodos hasta ahora estudiados, y que su evaluación por sustitución directa nos genera una forma indeterminada.
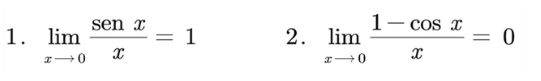
Ejemplo1:
Vamos a desarrollarlos uno a uno con los siguientes ejemplos:
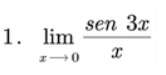
Solución:
En este caso el ángulo de la función trigonométrica es 3x, por lo que para poder aplicar el teorema correspondiente necesitamos que también en el denominador el valor del argumento sea 3x. Para poder satisfacer este requerimiento multiplicamos por 3 tanto en el numerador como en el denominador.
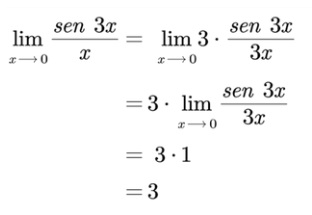
Ejemplo 2:
Desarrollar los límites de las siguientes funciones:
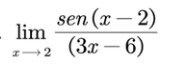
Solución:
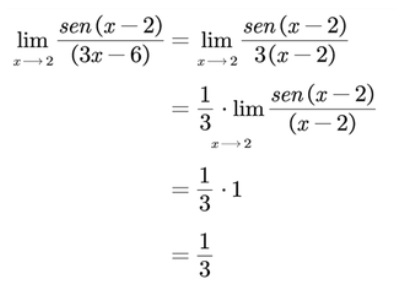
Ejemplo 3:
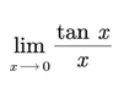
Solución:
La sustitución directa nos produce una forma indeterminada 0/0. Para ello utilizamos identidades trigonométricas para obtener una expresión equivalente tal como:
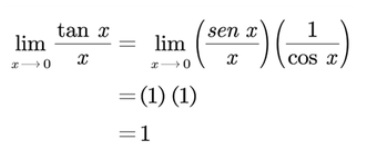
EJERCICIO 5: Resuelve los siguientes límites de funciones trigonométricas:
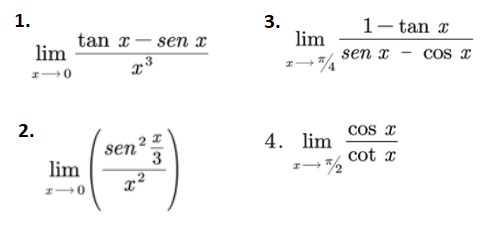
FUNCIONES CONTINUAS Y DISCONTINUAS
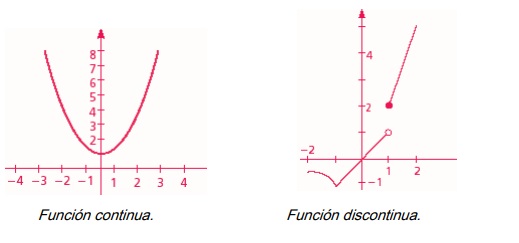
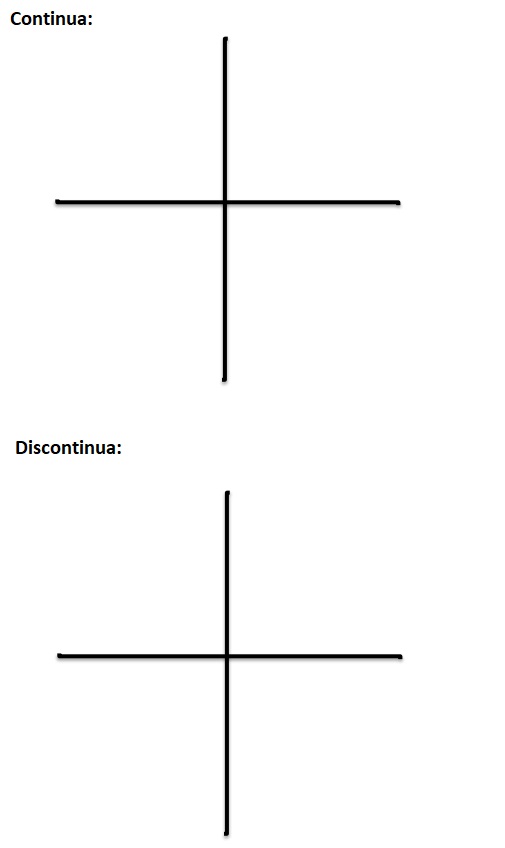
Intuitivamente, es fácil captar el concepto de continuidad. En términos sencillos, puede decirse que una función es continua en un intervalo cuando se puede dibujar sobre el papel a lo largo de dicho intervalo sin levantar el lápiz. Por otra parte, se considera que la función es continua en un intervalo (a, b) cuando es continua en todo punto 𝑥, tal que 𝑎 < 𝑥 < 𝑏.
Ejemplo 1:
Videos de apoyo:
Continuidad de una función: https://www.youtube.com/watch?v=ZEAPl6VN4JU
Discontinuidad: https://www.youtube.com/watch?v=pJ40TwrAZ9k
Ejercicio 6:
Dibujar dos ejemplos de continuidad de funciones, uno de continuidad y otro de discontinuidad.
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%): a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%): a. Prueba Bimestral
• Ser - Convivir (25%): a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION: Onceava Semana del Periodo
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
https://docs.google.com/forms/d/e/1FAIpQLSe8K6emBxx7juVipbyPzTOGq_10Rg7a2XDDfxaaipio4DKZTA/viewform?usp=pp_url
GUÍA DE APRENDIZAJE
En caso de no poseer internet, descarga aquí la guía de aprendizaje.




