Grado 10 - Estadística

CUARTO PERIODO

DBA 10. Propone y realiza experimentos aleatorios en contextos de las ciencias naturales o sociales y predice la ocurrencia de eventos, en casos para los cuales el espacio muestral es indeterminado 

ESTÁNDAR BÁSICO: Interpreto conceptos de probabilidad condicional e independencia de eventos.

CALCULO DE PROBABILIDADES

En el mundo de las probabilidades, es fundamental entender los conceptos de probabilidades conjuntas, marginales y condicionales. Estos términos nos permiten analizar y calcular la probabilidad de eventos en diferentes experimentos. En este artículo, te proporcionaremos una explicación detallada de cada uno de estos conceptos y te enseñaremos cómo calcularlos. ¡Empecemos! 

1. Probabilidades conjuntas:

Las probabilidades conjuntas se refieren a la probabilidad de que dos eventos ocurran simultáneamente en diferentes experimentos. En otras palabras, es la probabilidad de la intersección de dos eventos. Utilizamos la notación "P(A ∩ B)" o "P(A y B)" para representar la probabilidad conjunta. 

¿Cómo se calcula?

Para calcular las probabilidades conjuntas, necesitamos definir los eventos de cada experimento y conocer las probabilidades de cada evento. Para eventos mutuamente excluyentes y equiprobables, podemos utilizar una tabla de probabilidades para calcular las probabilidades conjuntas. En esta tabla, las filas representan los eventos del primer experimento y las columnas representan los eventos del segundo experimento. 

EJEMPLO:

Imaginemos que realizamos una encuesta a un grupo de personas sobre sus hábitos de consumo de café y té. Queremos calcular la probabilidad de que una persona Tome café y té. La tabla de probabilidades sería la siguiente: 

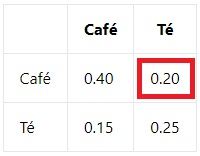
Basándonos en la tabla, la probabilidad de que una persona tome café y té simultáneamente es de 0.20. 

2. Probabilidades marginales:

Las probabilidades marginales representan la probabilidad de que un evento ocurra sin tener en cuenta los resultados de otro evento. En otras palabras, son las probabilidades individuales de cada evento en un experimento. Las probabilidades marginales se calculan sumando las probabilidades de los eventos en una fila o columna específica de la tabla de probabilidades conjuntas. 

¿Cómo se calcula?

Para calcular las probabilidades marginales, simplemente sumamos las probabilidades de los eventos en la fila o columna deseada. Por ejemplo, si queremos calcular la probabilidad marginal de tomar café, sumaríamos las probabilidades de los eventos que involucran el café en la tabla de probabilidades conjuntas. 

EJEMPLO:

Tomando el ejemplo anterior de la encuesta sobre hábitos de consumo de café y té, podemos calcular las probabilidades marginales de tomar café y té. La suma de las probabilidades en la fila correspondiente al café es de 0.60, lo que nos da la probabilidad marginal de tomar café. De manera similar, la suma de las probabilidades en la columna correspondiente al té es de 0.35, lo que nos da la probabilidad marginal de tomar té. 

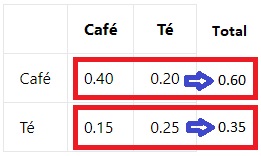
3. Probabilidades condicionales:

Las probabilidades condicionales se refieren a la probabilidad de que un evento ocurra dado que otro evento ya ha ocurrido. Es la forma de medir cómo un evento puede afectar la probabilidad de otro evento. Utilizamos la notación "P(B|A)" para representar la probabilidad condicional de que el evento B ocurra dado que el evento A ha ocurrido. 

¿Cómo se calcula?

Para calcular las probabilidades condicionales, primero necesitamos conocer la probabilidad conjunta de los dos eventos y la probabilidad marginal del evento condicionante. Luego, dividimos la probabilidad conjunta entre la probabilidad marginal del evento condicionante. Esta fórmula nos dará la probabilidad condicional del evento deseado. 

EJEMPLO:

Supongamos que realizamos una encuesta a estudiantes universitarios sobre si han copiado en un examen. Además, separamos los resultados de acuerdo al género de los estudiantes. Queremos calcular la probabilidad de que un estudiante sea hombre dado que ha copiado en un examen. La tabla de probabilidades conjuntas y marginales sería la siguiente: 

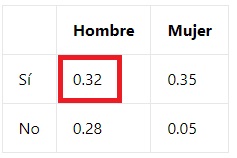
Para calcular la probabilidad condicional de que un estudiante sea hombre dado que ha copiado en un examen, dividimos la probabilidad conjunta de ambos eventos ("Hombre y Sí") entre la probabilidad marginal de haber copiado en un examen. Esto nos dará la probabilidad condicional deseada. 

Ventajas y desventajas de utilizar probabilidades

Ventajas:

• Las probabilidades nos permiten cuantificar la incertidumbre y tomar decisiones informadas.
• Ayudan a predecir resultados en diferentes experimentos y escenarios.
• Proporcionan una base sólida para el análisis estadístico.

Desventajas:

• Las probabilidades pueden ser difíciles de interpretar y comprender para algunas personas.
• Las probabilidades dependen de ciertas suposiciones y pueden no ser 100% precisas en la vida real.
• El cálculo de probabilidades puede volverse complicado cuando los eventos son independientes o se tienen múltiples variables.

ACTIVIDAD 1. Cuestionario

1. ¿Por qué es importante entender las probabilidades conjuntas?

2. ¿Cómo se calculan las probabilidades marginales?

3. ¿Cuál es la diferencia entre probabilidades condicionales y conjuntas?

4. Te invito a observar los temas en los siguiente videos y desarrollar los ejercicios que allí se encuentran:

https://matemovil.com/probabilidad-condicional-ejercicios-resueltos/ 

https://drive.google.com/file/d/195nkKxt0bL2sOrrI-MRrEOwZgOJJsUML/view 

ACTIVIDAD 2.

1. Las instituciones bancarias emplean modelos computarizados de cr´edito con el prop´osito de dar un determninado puntaje a todas las solicitudes de pr´estamo. Este puntaje se emplea como una ayuda para ´ decidir cuando se otorga un pr´estamo. Se tiene: El 3 % de todos los pr´estamos que se otorgan presentan problemas de incumplimiento de pago. Los modelos son precisos en un 80 % al predecir menos cr´editos. (Puntuaci´on favorable dado el cumplimiento del pago). Si el 85 % de todas las solicitudes reciben puntuaciones favorables por los modelos computarizados y se les otorga el pr´estamo. 

Determinar la probabilidad de que una solicitud que recibe una puntuaci´on favorable y a la que se le otorga el pr´estamo, no presente ning´un problema para el pago de ´este. 

2. Una planta recibe reguladores de voltaje de dos diferentes proveedores, B1 y B2. El 75 % de los reguladores se compra a B1 y el 25 % de los reguladores se compra a B2. El porcentaje de reguladores defectuosos de B1 es 8 %, el porcentaje de reguladores defectuosos de B2 es 10 %. 

Determinar la probabilidad de que funcione un regulador de voltaje de acuerdo a las especificaciones (no sea defectuoso).