Grado 10 - Geometría
Tercer Periodo
Conocimientos previos
1. Figuras bidimensionales: Que tiene dos dimensiones, largo y ancho. Elementos
bidimensionales, se requieren dos coordenadas para lograr la
especificación de un punto. Los polígonos, como los cuadrados o los
triángulos, son bidimensionales.
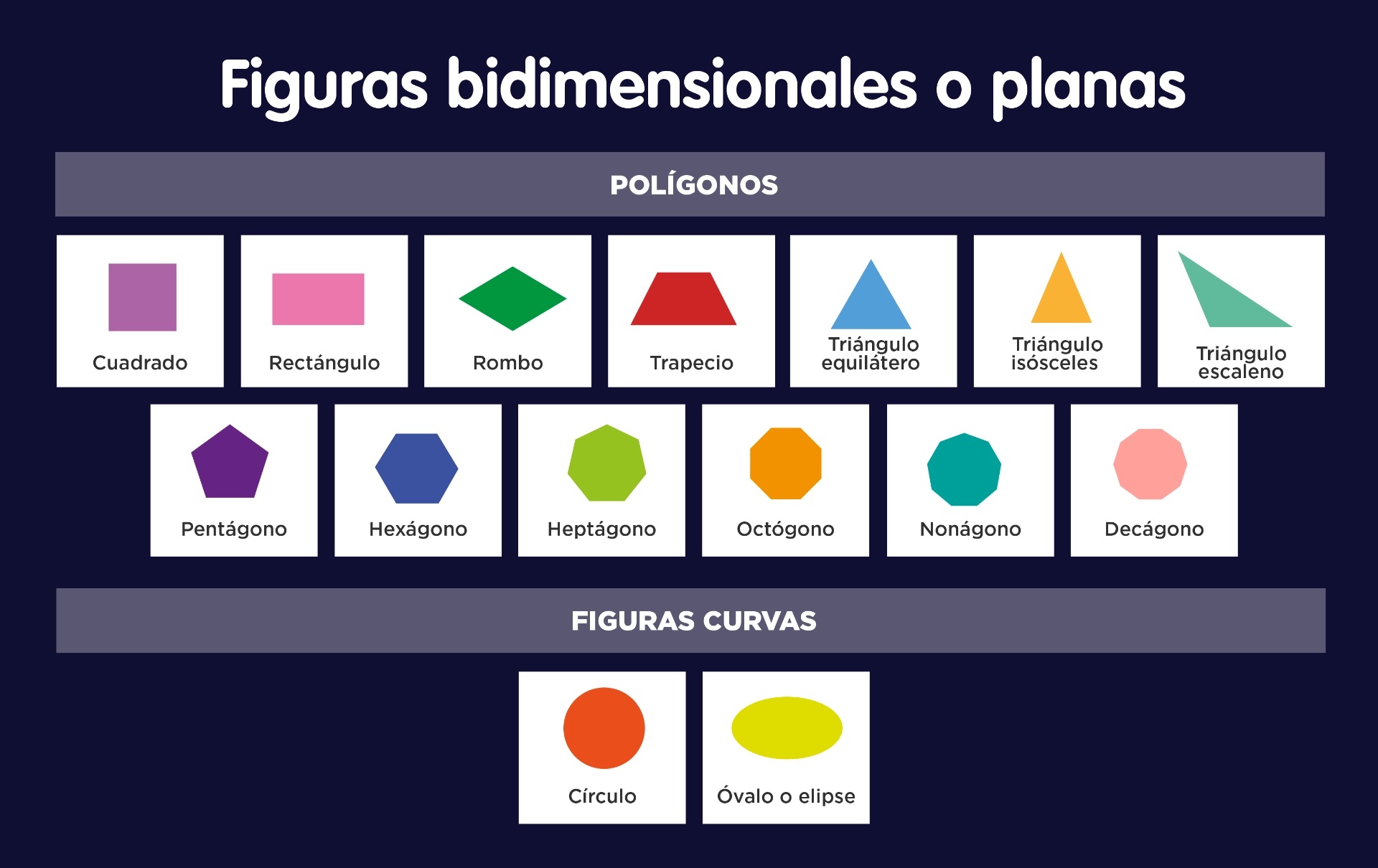
2. Figuras tridimensionales: El adjetivo tridimensional se utiliza para calificar a aquello que tiene tres dimensiones, estas son: se encuentran presentes la altura (o la profundidad), el largo y el ancho. En geometría son tridimensionales las siguientes figuras geométricas:
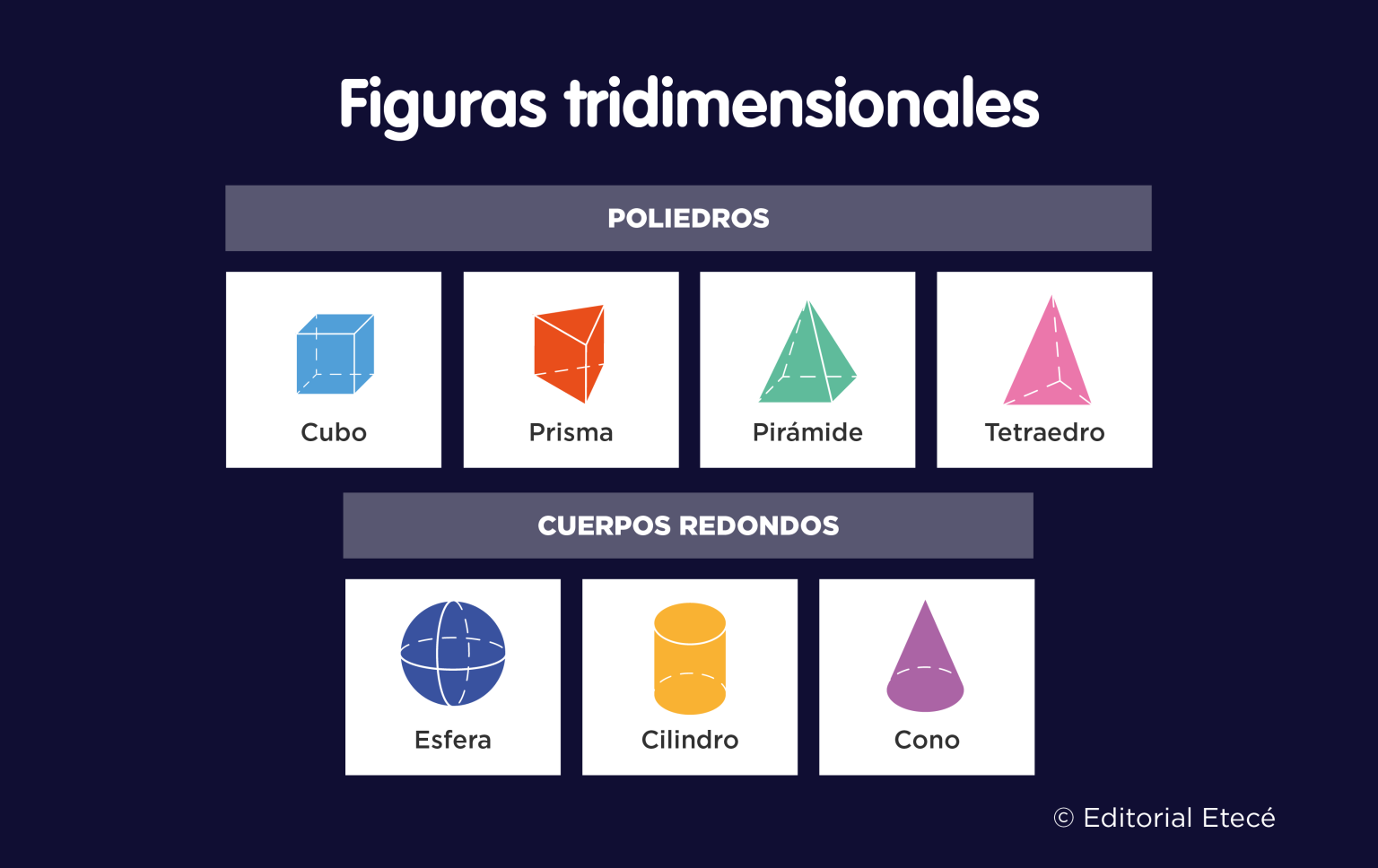
• Poliedros de caras planas:
o Pirámides
o Cubo
o Prismas
o Tetaedro
• Superficies curvas:
o Cilindro
o Conos
o Esfera
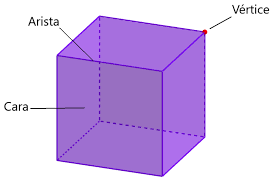
Vocabulario de las figuras tridimensionales o volumétricas:
- Cara. Es cada figura plana que forma una figura tridimensional.
- Arista. Es la línea en la que se unen dos caras.
- Vértice. Es el punto en el que se unen tres o más caras.
ACTIVIDAD1. Resuelve en tu cuaderno
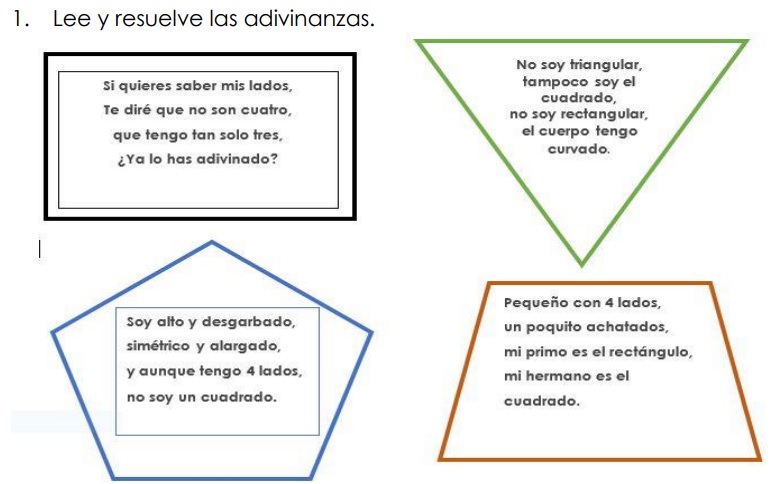
2. Dibuja dos objetos de tu casa que tenga forma cuadrada, rectangular, circulo o triangular. Recuerda utilizar la regla.
3. Toma una caja (gelatina, medicamente u otra), luego recorta la caja
por las aristas y por último describe, ¿Por Cuántas figuras geométricas está
compuesta la caja?
CIRCUNFERENCIA Y CÍRCULO
1. Circunferencia:
La circunferencia es el lugar geométrico formado por todos los puntos del plano que están a una misma distancia de otro punto llamado centro (O).
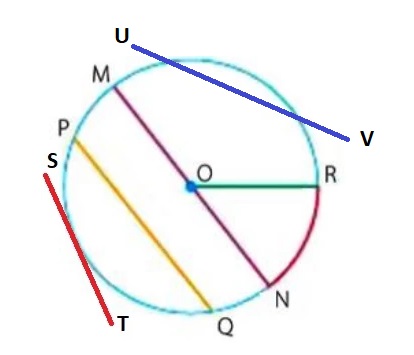
En la circunferencia se reconocen los siguientes elementos:
• Centro (O): Punto del cual equidistan todos los puntos de la circunferencia.
• Radio (𝑂𝑅): Segmento que une el centro con un punto cualquiera del borde de la circunferencia. Generalmente se denota con la letra r.
• Cuerda (𝑃𝑄): Segmento que une dos puntos de la circunferencia.
• Diámetro (𝑀𝑁): Cuerda que une dos puntos de la circunferencia que pasa por el centro de la misma. Se suele denotar con la letra D.
• Arco (𝑁𝑅): Porción del borde de la circunferencia comprendida entre dos de sus puntos. Se nombran con letras
en mayúscula y en sentido antihora
• Tangente (ST): Línea recta que toca el círculo solamente en un punto. Este punto es llamado el punto de tangencia.
• Secante (UV): Línea recta que atraviesa la circunferencia cortandola en dos puntos.
Sino te quedó claro el tema te invito a observar el siguiente video:
ACTIVIDAD 2:
1. Construye una circunferencia con las medidas indicadas
a. Circunferencia O con r = 6 cm b. Circunferencia Q con d = 6 cm
* Pinta con color rojo 4 diámetros e identifica sus medidas.
* Pinta además, 5 radios azul. Identificando también sus medidas.
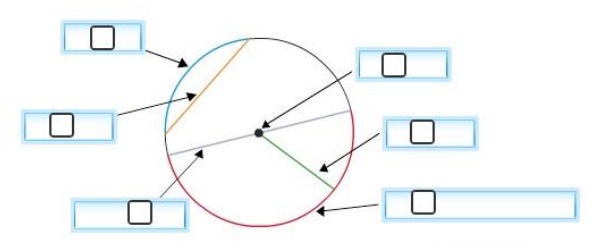
2.- Escribe en tu cuaderno el nombre de cada elemento de la circunferencia.

Perímetro de un círculo:
El perímetro de un círculo de radio r es la longitud de su lado (borde):

Como el diámetro de un círculo es dos veces su radio, d=2.r, podemos escribir el perímetro como
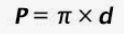
Área de un círculo:
El área de un círculo es su superficie:

ACTIVIDAD 3:
1. Observa la imagen de un blanco para jugar a la puntería y contenta las respuestas en tu cuaderno:

Registra los datos que se piden en la tabla:
* Mide con una regla el diámetro de tres de los círculos que se pueden identificar en el blanco de tiro y regístralo.
* Para medir el perímetro de cada círculo que escogiste anteriormente, usa un trozo de hilo para rodear el contorno de cada uno y luego mide el hilo con una regla. Registra tus resultados en la tabla.
* Con una calculadora realiza la división Perímetro : Diámetro. Escribe cada resultado con dos
decimales.

¿Observa alguna relación entre los resultados obtenidos? Escribe tu conclusión.
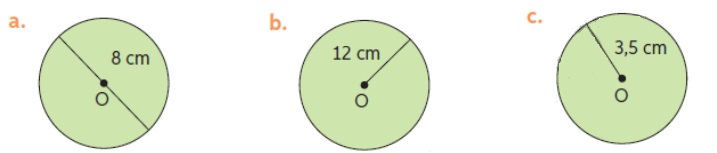
2. Determina el perímetro de los siguientes círculos. Considera π ≈ 3,14
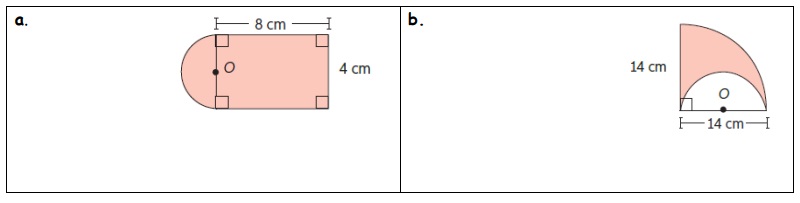
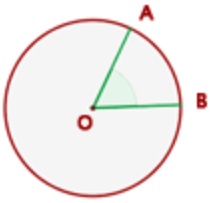
3. Calcula el perímetro de figuras sombreadas.
Ángulos y segmentos en el círculo
1. Ángulo Central.
El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.
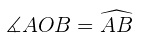
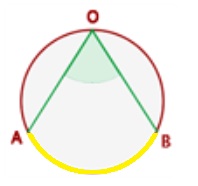
• 2. Ángulo inscrito: Formado por dos cuerdas que parten de un mismo punto de la circunferencia.
Mide la mitad del arco que abarca.
Mide la mitad del arco que abarca.
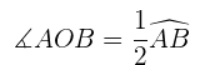
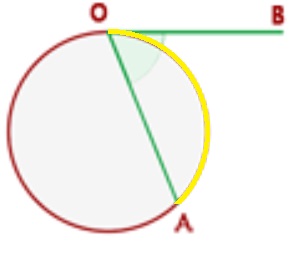
• 3. Ángulo semi-inscrito: El vértice de ángulo semi-inscrito hace referencia a una semirrecta que está en la circunferencia (secante) y la otra semirrecta tangencial a ella.
Mide la mitad del arco que abarca.
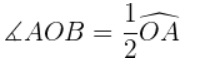
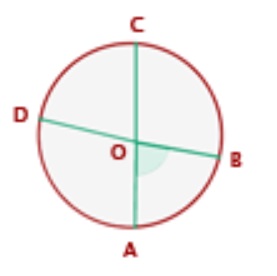
• 4. Ángulo interior: Su vértice es interior a la circunferencia y sus lados secantes a ella.
Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.
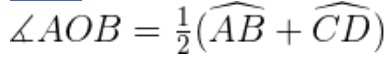
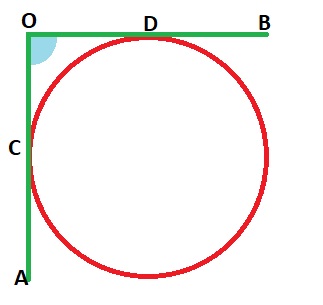
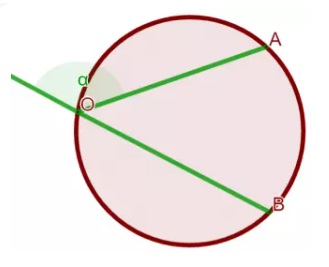
• 5. Ángulo exterior:
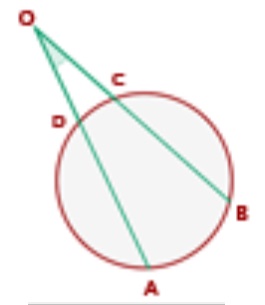
a. Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son secantes a ella
b. Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son uno tangente y otro secante a ella
c. Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son tangentes a ella
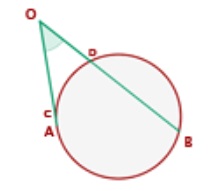
• 6. Ángulo Ex-inscrito: El ángulo ex-inscrito tiene su vértice en la línea del de la circunferencia y es el ángulo suplementario al ángulo inscrito.
Mide la mitad del arco que no abarca el ángulo inscrito.
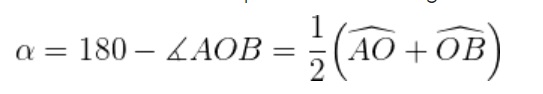
ACTIVIDAD 4. Responde en tu cuaderno las actividades del siguiente link:
TEOREMAS EN LA CIRCUNFERENCIA
1. Teorema de las cuerdas
Si dos cuerdas se cortan en el interior de una circunferencia, el producto de los segmentos determinados en cada una de ellas, por el punto de intersección, es constante
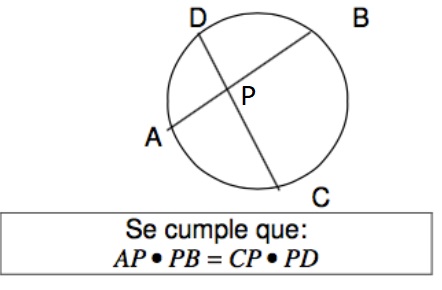
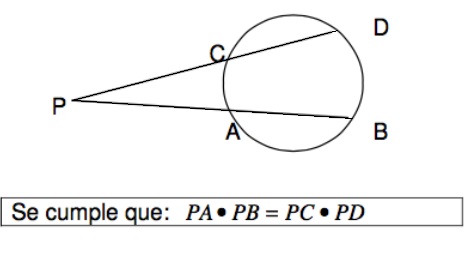
2. Teorema de las secantes
Si desde un punto exterior a una circunferencia se trazan dos secantes a ella, el producto de cada secante entera por su segmento exterior, es constante.
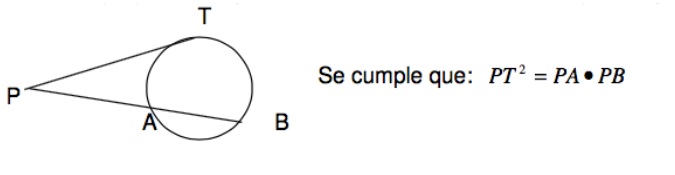
3. Teorema de la tangente y de la secante
Si desde un punto exterior a una circunferencia se traza una tangente y una secante, la tangente es media proporcional geométrica entre la secante entera y su segmento exterior
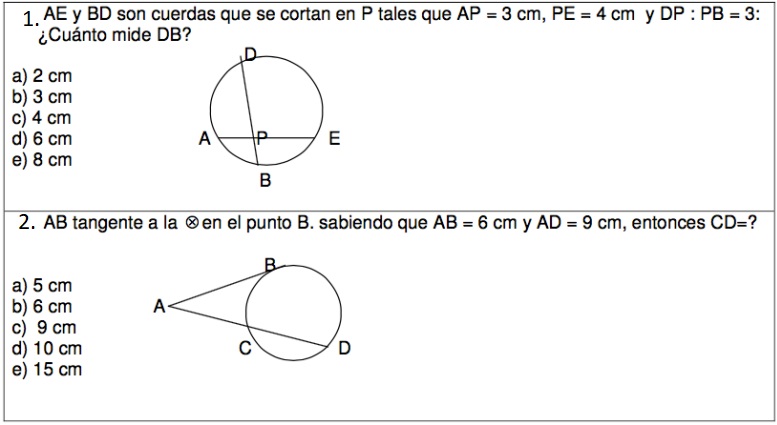
ACTIVIDAD 5. De acuerdo a lo anterior, responde en tu cuaderno las siguientes actividades (Comparando la imagen):
TRANSFORMACIONES GEOMÉTRICAS
(Traslación, rotación, reflexión y dilatación o contracción)
La traslación, la rotación y la reflexión son movimientos que se realizan con una figura en un plano; a la izquierda, a la derecha, diagonal, arriba y abajo.
1. TRASLACIÓN:
Es el desplazamiento hacia la derecha, hacia la izquierda, arriba, abajo, diagonal de una figura plana; a lo largo de una recta, con distancia y dirección definida.
Procedimiento para trasladar una figura:
- Punto de partida
- Punto de llegada
- Y la dirección en que se mueve la figura
Ejemplo 1:
Trasladar la figura 12 unidades a la derecha

Para trasladar se inicia contando las unidades, desde el inicio de la figura a trasladar.
2. ROTACIÓN:
Es el giro de una figura plana alrededor de un punto llamado Centro de Rotación; y a lo largo de un ángulo de giro, sin que cambien sus características.
Nota: Antes de hacer los EJEMPLOS de rotación de las figuras se debe recordar que una circunferencia mide 360° grados.
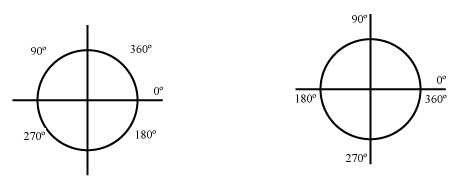
Ejemplo 2:
Rotar la figura hacia la derecha
3. REFLEXIÓN:
Es invertir la posición de una figura con respecto a una recta llamada que de simetría.
Cuando una figura se refleja en un espejo, se invierte su imagen; es decir, si estaba hacia arriba se ve hacia abajo.
Aquí la montaña es una figura simétrica que se invierte o se refleja en el agua, como si fuera un espejo.
4. DILATACIÓN:
Una dilatación hace que una figura sea más grande o menor de tal manera que la nueva imagen tenga la misma forma que la original.
Ej: El cuadrilátero EFGH\) tiene vértices E(−4,−2) F(1,4) G(6,2) H(0,-4). Dibuja la dilatación con un factor de escala de 1.5.
Solución:
Recuerda que para dilatar algo en el plano de coordenadas, multiplica cada coordenada por el factor de escala.
Para esta dilatación, el mapeo será ((x, y)\ fila derecha (1.5x, 1.5y).
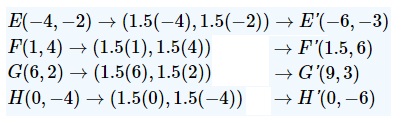
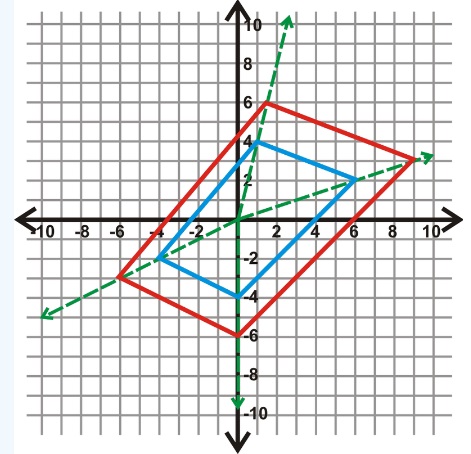
En la gráfica anterior, el cuadrilátero azul es el original y la imagen roja es la dilatación.
Sino te quedó claro el tema, te invito a observar los siguientes videos:
ACTIVIDAD 6. Para realizar en tu cuaderno:
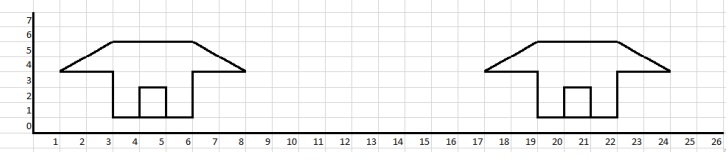
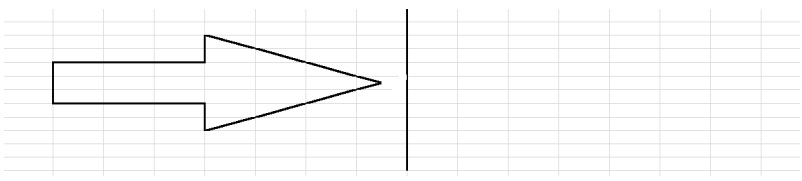
1. Traslada la figura nueve unidades a la derecha hasta que complete la cenefa:
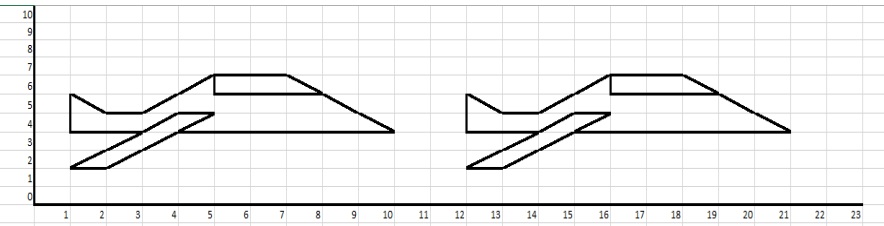
2. Describe la traslación realizada por el avión:
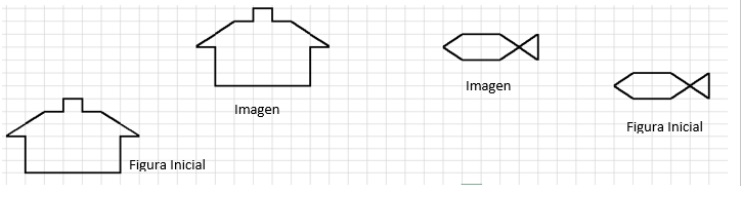
3. Identifica y escribe las traslaciones aplicadas a las siguientes figuras:
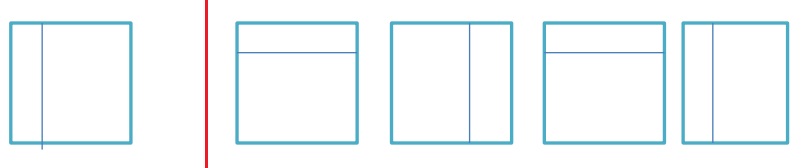
4. Gira 90° grados cada figura para completar las series:
5. Dibuja la imagen reflejada de la figura:
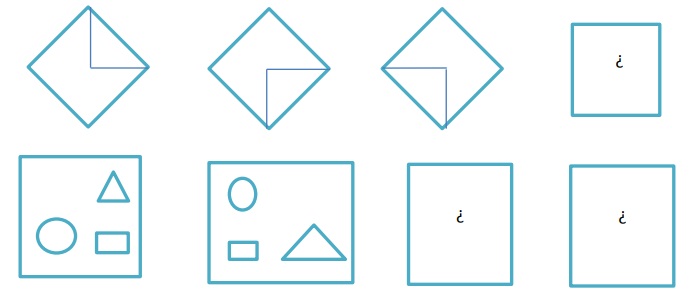
6. Elige la figura que representa una reflexión:
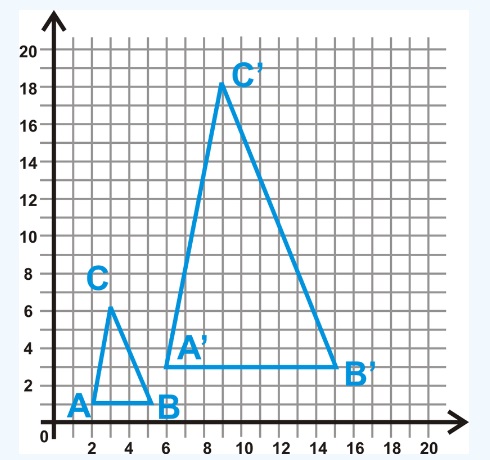
7. Determinar las coordenadas ΔABC ΔA'B'C' y encontrar el factor de escala.
5. COMPOSICIÓN DE TRANSFORMACIONES:
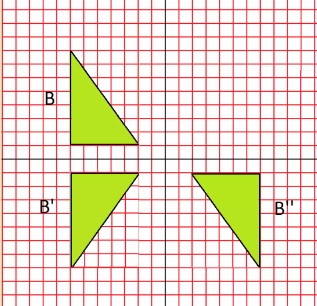
Si al resultado de una reflexión se le aplica se le aplica otra reflexión, se afirma que hay una composición de reflexiones. Si al resultado de una traslación se le aplica se le aplica otra traslación, se afirma que hay una composición de traslaciones. De la misma forma también ocurre con la rotación.
Ejemplo de una composición de reflexión:
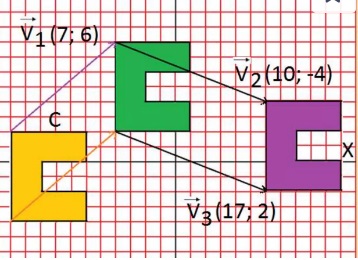
Ejemplo de una composición de traslación:
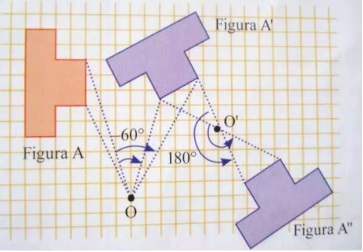
Ejemplo de una composición de rotación:
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad: