Grado 9 - Geometría
Periodo 3
Temas Parte1:
- Traslaciones, reflexiones y rotaciones
- Dilataciones y contracciones
- Simetría y congruencia en transformaciones
1. TRASLACIÓN
Las traslaciones pueden entenderse como movimientos directos sin cambios de orientación, es decir, mantienen la forma y tamaño de las figuras u objetos trasladados a las cuales deslizan según un vector. Una traslación desplaza cada punto de una figura la misma cantidad en una misma dirección.
¿Has intentado crea runa obra de arte alguna vez?
Tanya encontró un sector en el que podías crear una obra de arte usando un computador. Estas graficas se pueden crear y modificar usando un programa. Tanya uso el programa para crear esta imagen.
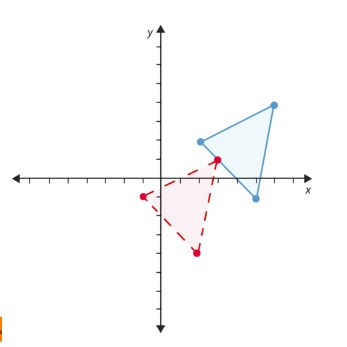
Gráfico 1.
Creó una imagen que comenzó en la posición azul y se movió hacia la posición roja.
¿Sabes cómo se les llama a estas dos figuras?
En el plano cartesiano puedes cambiar las figuras de muchas maneras. Esta Sección te enseñara cómo.
Orientación
Al realizar una traslación , desplazamos una figura a la derecha, la izquierda, hacia arriba o abajo. Esto implica que las coordenadas de los vértices cambiaran. Observa el siguiente diagrama.
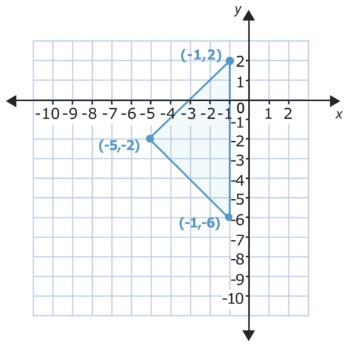
Gráfico 2
Ahora realicemos una traslación de la figura 2.
Podemos elegir cuantas posiciones y en qué dirección mover el triángulo. Si movemos el triángulo 3 posiciones hacia abajo, todos los vértices del triángulo en el eje Y disminuyendolo en 3. Esto quiere decir que los pares ordenados de los nuevos vértices cambian. Específicamente, la coordenada en Y se le restan 3 puntos pero el eje X permanece igual.
Ejercicio 1.
Veamos cómo funciona utilizando una herramienta llamada Geogebra.
Hagamos lo siguiente:
1. Vamos al link: https://www.geogebra.org/calculator
2. Seleccionamos en la sección polígonos la opción polígonos
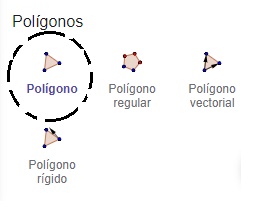
3. Marcamos los puntos que aparecen el el gráfico 2 (Nota: Si no aparece la escala de la cuadrícula de 1 en 1, hacemos clic derecho con el mouse en la pizarra que es la parte central y seleccionamos Propiedades; y en eje X y Y le cambiamos el número de cuadrículas
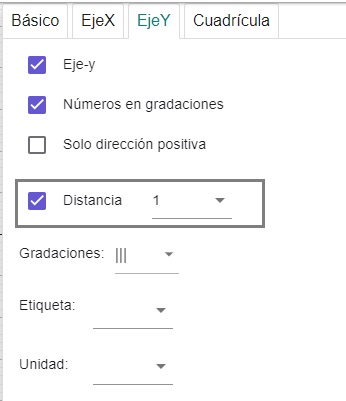
4. Una vez realizado el polígono seleccionamos la opción vector (en la sección rectas) y buscamos cualquier punto y lo desplazamos hacia abajo 3 casillas
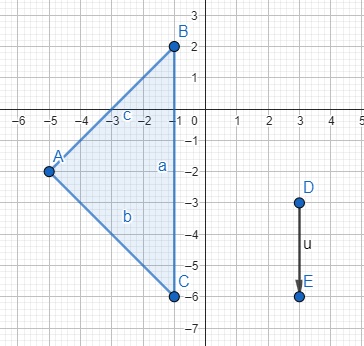
5. Buscamos en la sección transformaciones la opción traslación. Allí seleccionamos primero la imagen del polígono y luego el vector de traslación, quedando de la siguiente manera:
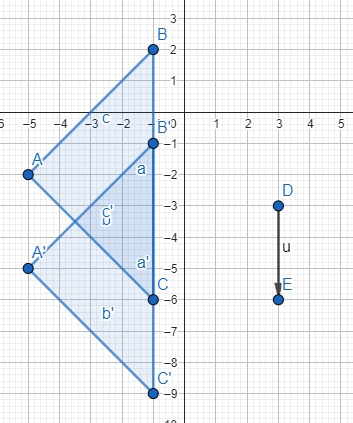
Podemos notar cómo cambian las coordenadas de Y. Compara los puntos superiores. El valor de Y original es (-1,2), luego de moverlo cambia a (-1,-1). La coordenada Y disminuye en 3 posiciones hacia abajo. Ahora compara las puntas izquierdas de cada triángulo. El valor de Y original es (-5,-2) luego de moverlo cambia a (-5,-5). Nuevamente, la coordenada Y de la parte de abajo es (-1,-6), luego de moverlo cambia a (-1,-9). En cada punto, la coordenada Y disminuye en 3 puntos, mientras que la coordenada X permanece igual.
2. REFLEXIÓN
Una reflexión es un mapeo de un espacio euclidiano a sí mismo que es una isometría con un hiperplano como un conjunto de puntos fijos; este conjunto se llama eje o plano de reflexión. En otras palabras es el antireflejo en un espejo o rotación sobre un eje de la figura.
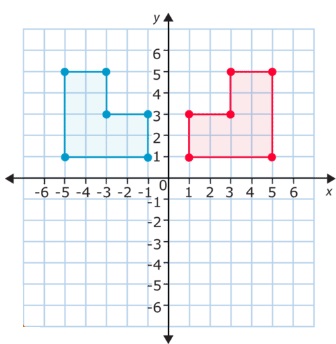
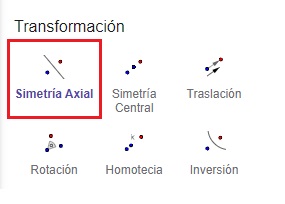
Ejercicio 2.
Para realizar este ejercicio en Geogebra, lo hacemos de la misma forma que lo hicimos en el punto 1 de traslación pero celeccionamos la opción simetria axial en la opción transformación. Como segunda medida tocamos el polígono y luego el eje donde queremos reflejarlo (X ó Y), quedando de la siguiente manera:
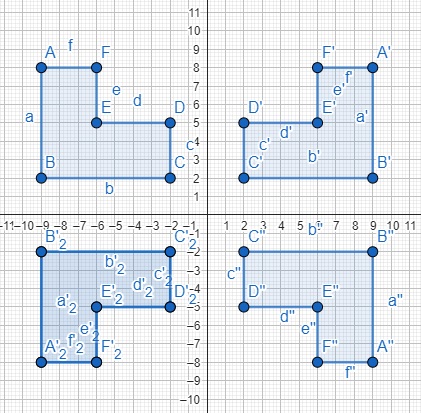
3. ROTACIÓN
Ahora grafiquemos el tercer tipo de transformación: La rotación. Una rotación es una transformación que gira la figura en sentido del reloj o contra el reloj. La figura de abajo ha sido rotada. ¿Cuáles son sus coordenadas nuevas?
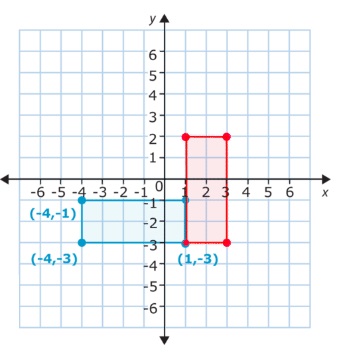
Las coordenadas nuevas de los vértices del rectángulo son (1, -3), (1, 2), (3, 2) y (3, -3). En este caso, tanto las coordenadas de X como las de Y cambiaron.
Toda rotación es un movimiento de un cierto espacio que conserva al menos un punto en el cual gira, por ejemplo, el movimiento de un cuerpo rígido alrededor de un punto
A diferencia de una traslación o reflexión, una rotación cambia ambas coordenadas de un par ordenado. Ahora observa con atención. ¡Uno de los puntos no cambió! Eso se debe a que la figura rotó en ese punto. Imagina que pones tu dedo en esa esquina del rectángulo y lo haces girar. Eso sucede con las rotaciones. El rectángulo rotó 90° en el sentido del reloj.
¿Cómo graficamos una rotación?
Al graficar una rotación, primero debemos saber cuánto rotará la figura. Al rotar el rectángulo de arriba en 90° , este queda en posición vertical. Al rótalo en 180° vuelve a quedar horizontal. También debemos saber sobre qué punto se rotará. Este es el punto que se mantendrá igual.
Ejemplo (Utilizando Geogebra)
1. Realizamos la figura, Ej: Un poligono como el siguiente:
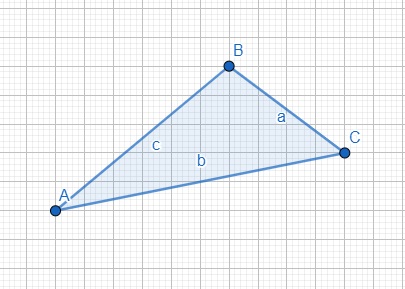
2. Para este ejemplo vamos a utilizar un deslizador que se encuentra en herramientas básicas
3. Lo ubicamos en la parte superior derecha y digitamos los siguientes datos:
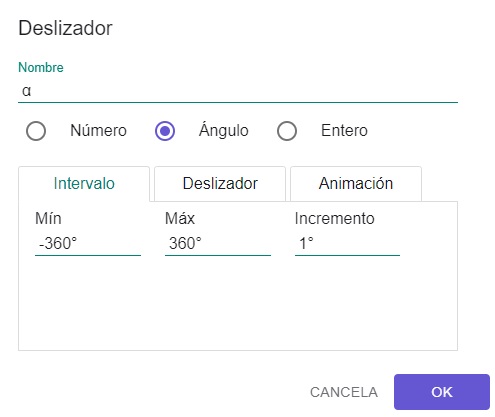
Observa que si mueves el círculo que aparece en el deslizador el muestra los grados de -360 a 360.
4. Utilizamos la herramienta rotación que se ubica en el grupo transformación.
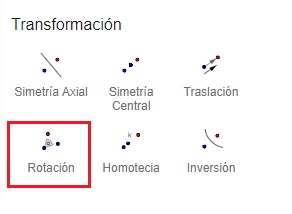
Allí me pide que seleccione el objeto a rotar, un punto de rotación y amplitud del ángulo.
En este caso vamos a seleccionar la figura y como segunda medida selecciones el punto A. Inmeditamente nos saldrá la siguiente imagen:
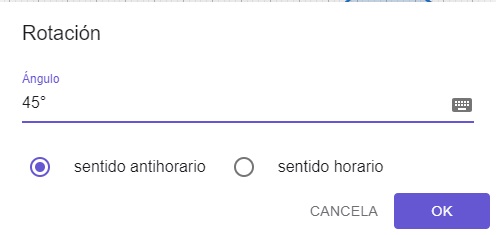
Del cual borraremos los 45° y en el dibujo del teclado que aparece al lado derecho, vamos a selecciona el ángulo del deslizador que se llama alfa (α), como lo muestra la imágen
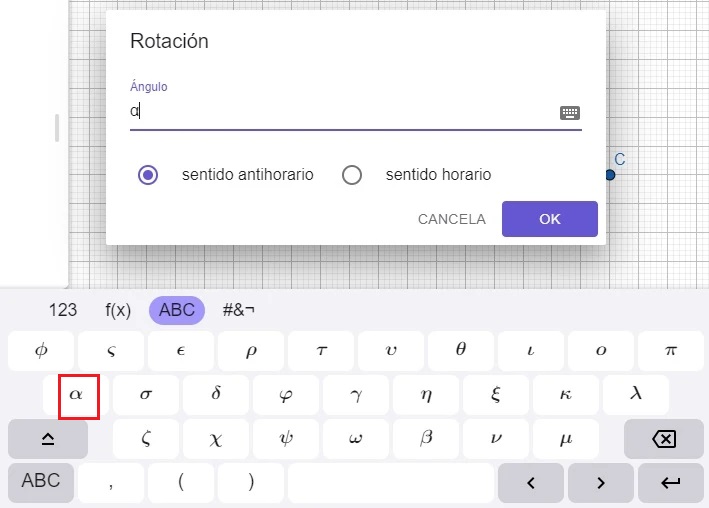
Ahora vamos a mover el deslizador y veras como la figura rota sobre el eje A:
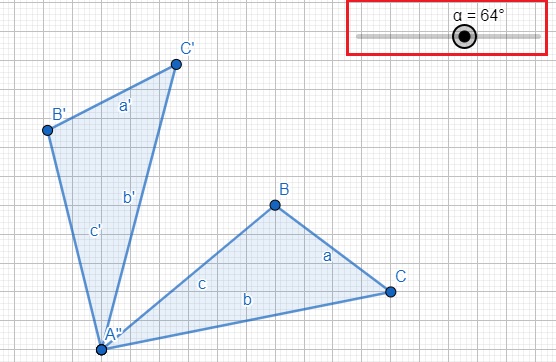
Nota: Si lo mueves a la derecho, el movimiento será positivo o antihorario o contrario a las manecillas del reloj, de lo contrario será negativo.
Si quieres realizar una animación hacemos lo siguiente:
1. Damos clic sobre el punto C´' y seleccionamos mostrar rastro

2. Damos clic derecho sobre el deslizador y seleccionamos animación:

Esta opción dejará un rastro de 360°
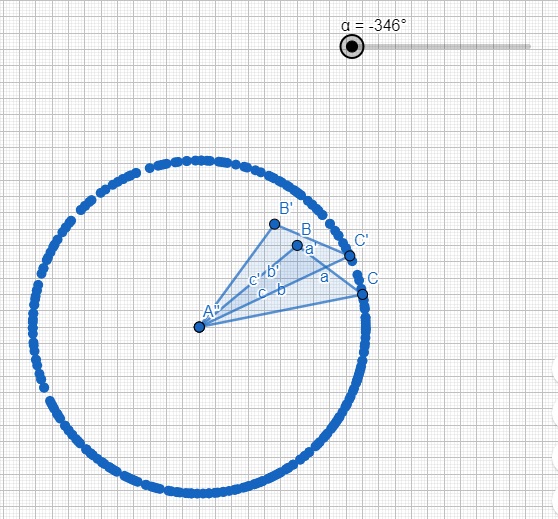
Ejercicio 3:
Realiza la rotación sobre el punto B del siguiente polígono regular utilizando deslizadores en geogebra:
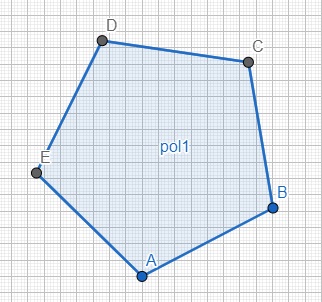
Dilataciones y contracciones
Una dilatación es cuando hacemos más grande una figura (Ampliación) y cuando la hacemos pequeña se llama contracciones (Reducción).
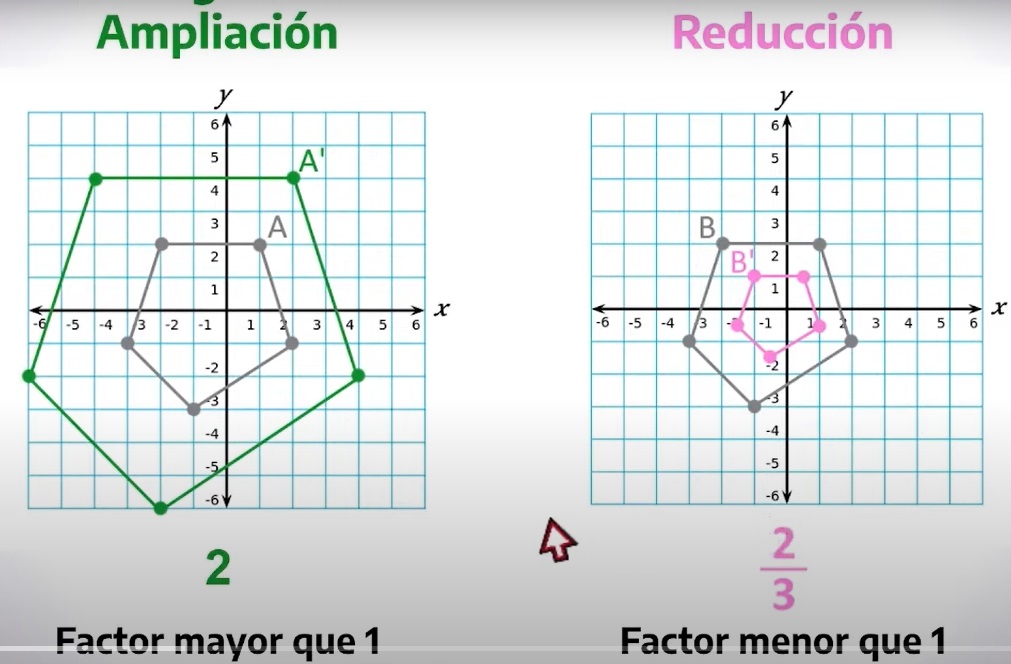
También existen dilataciones o contracciones con respecto al origen que es el punto cero (0).
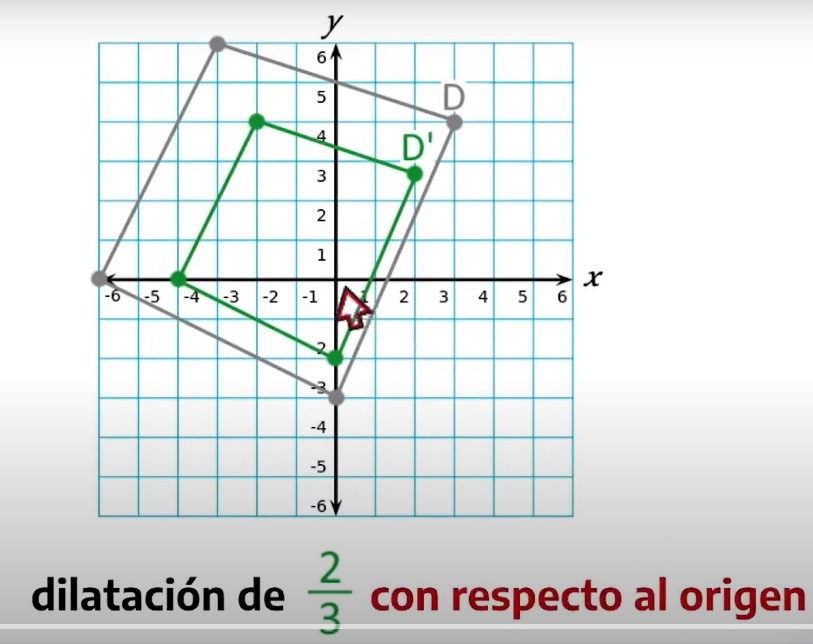
Cuando hablamos de dilataciones es posible realizarla sobre cualquier punto
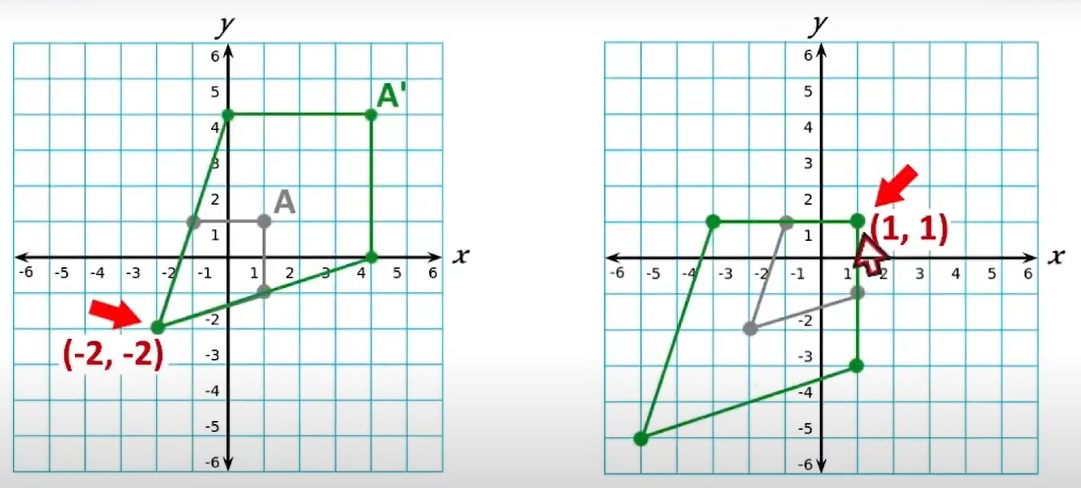
Cómo se hacen las dilataciones:
1. Primero escribimos las coordenadas originales. Ej:
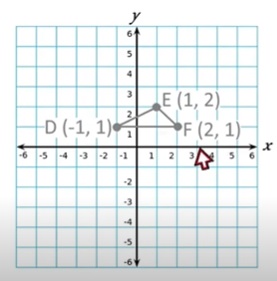
2. Multiplicamos cada coordanada por el factor escalar, Ej: 3
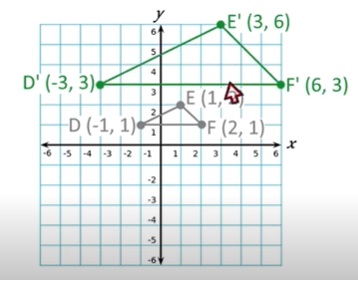
Cómo se hacen las contracciones:
Primero escribimos las coordenadas originales. Ej:
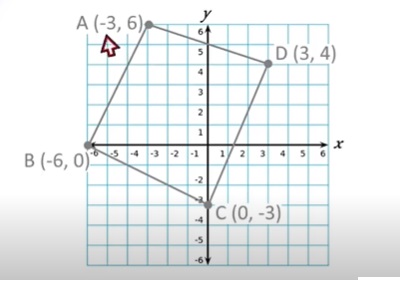
2. Multiplicamos cada coordanada por el factor escalar, Ej: 2/3

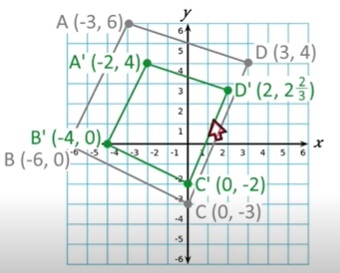
Ejercicio 4:
Realiza en papel milimetrado o en tu cuaderno cuadriculado un tríangulo con las siguiente coordenadas:
(2,0)(-2,-4)(4,-2),
1. realizar una dilatación con factor escalar de 2.
2. y una contracción de 2/3
Simetría y congruencia en transformaciones
Desde el punto de vista geométrico, un objeto posee simetría si existe una "operación" o "transformación" (como una isometría o una transformación afín) capaz de aplicar su figura sobre sí misma. De forma análoga, se dice que el objeto es simétrico porque posee una invarianza con respecto a la transformación
1. Simetría Axial:
Se da cuando los puntos de una figura coinside con los puntos de otra, tomando como referencia una línea que se llama EJE DE SIMETRÍA. Ej:
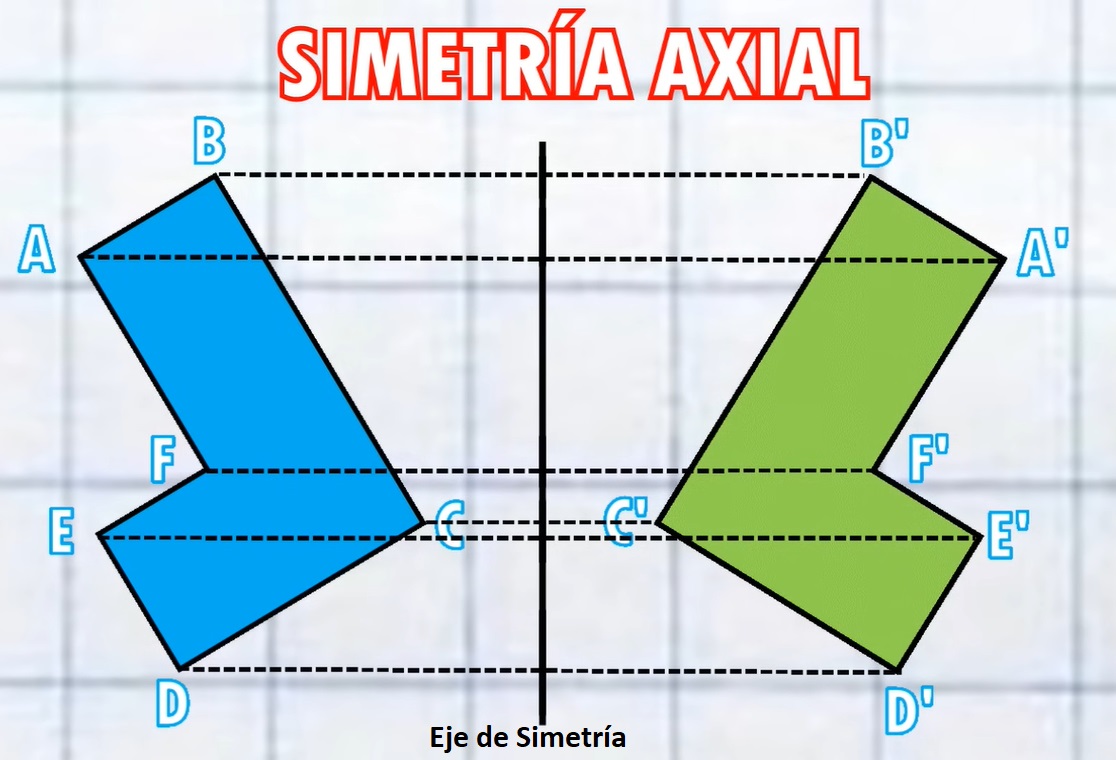
Es también llamado efecto espejo.
2. Simetría Central:
Es el reflejo de una imagen tomando como referencia un solo punto llamado punto de simetría. Ej:
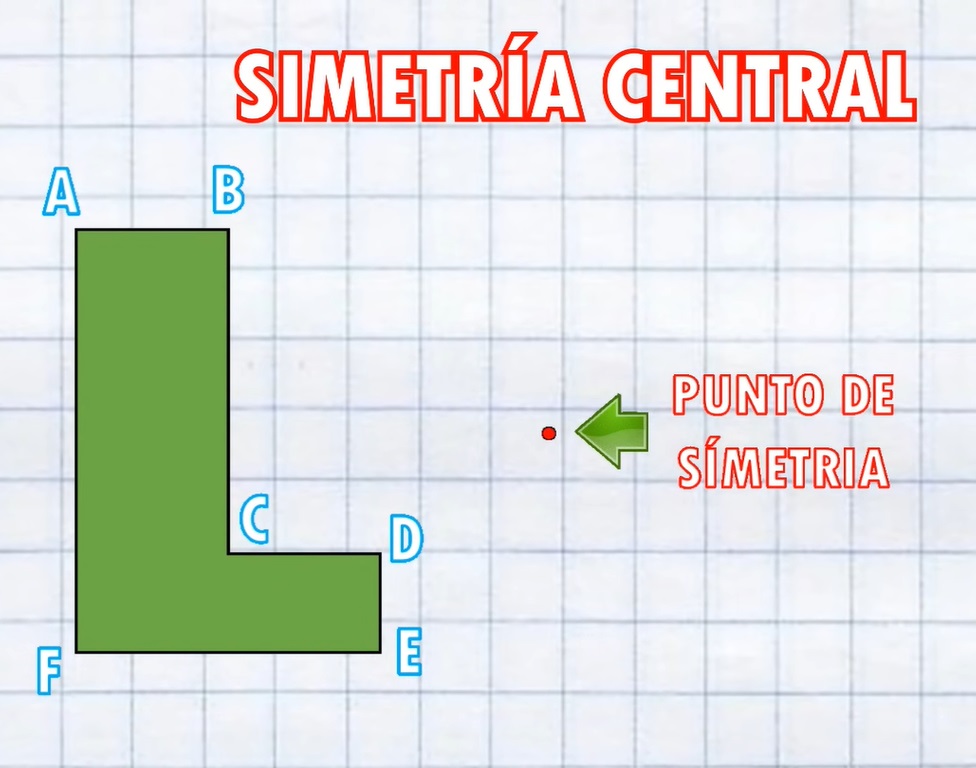
Reflejamos todos los vertices a través del punto con la misma distancia y luego unimos los puntos:
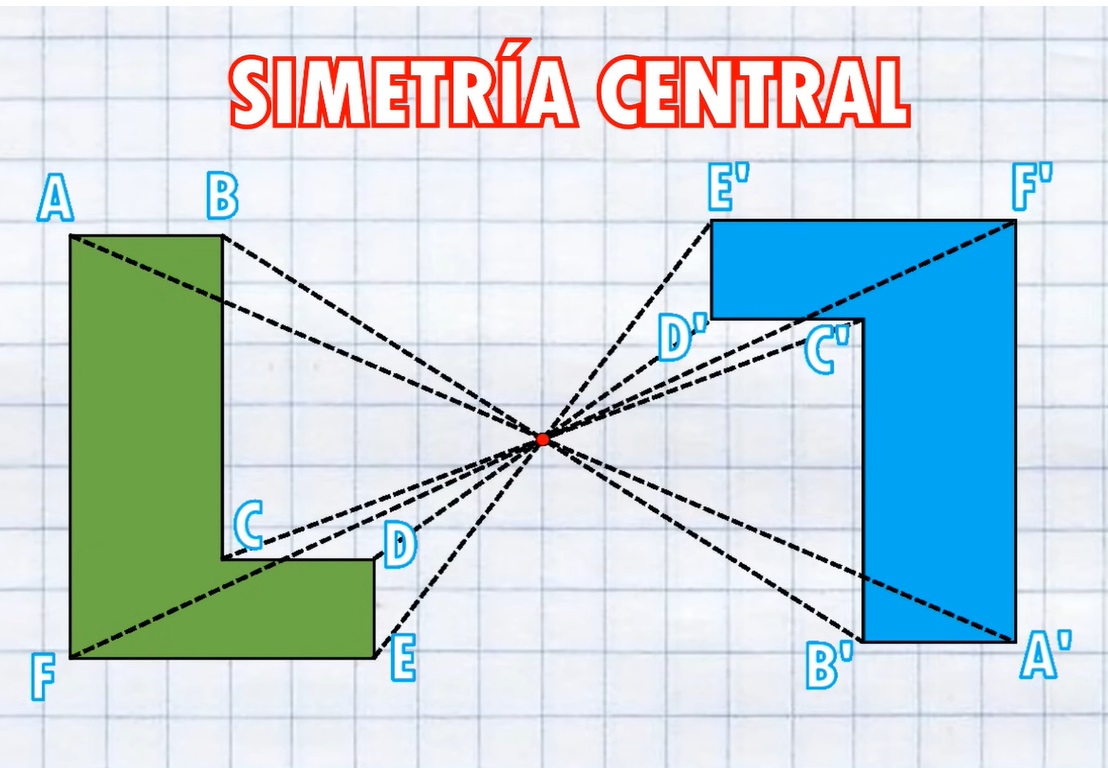
Esto es lo que llamamos un giro de 180°, es decir, la figura queda de cabeza.
Ejercicio 5. Simetría Axial.
1. Un artista tiene una obra sobre la pared, sin embargo quiere tener la misma obra pero reflejada respecto a una lámpara de piso. ¿Cuál es la opción que representa la simetría axial?
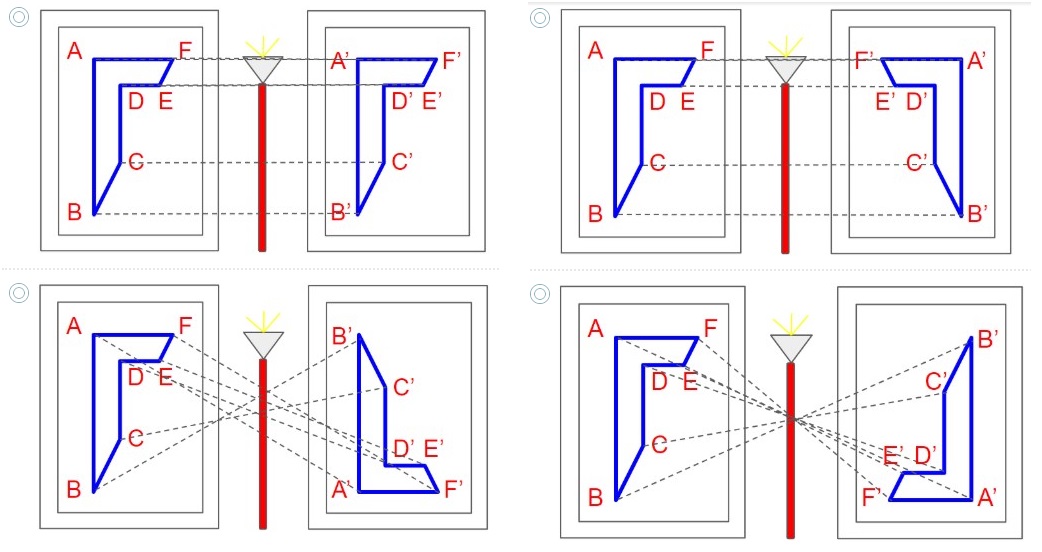
2. Un artista tiene una obra sobre la pared, sin embargo quiere tener la misma obra pero reflejada respecto a una lámpara de piso. ¿Cuál es la opción que representa la simetría axial?
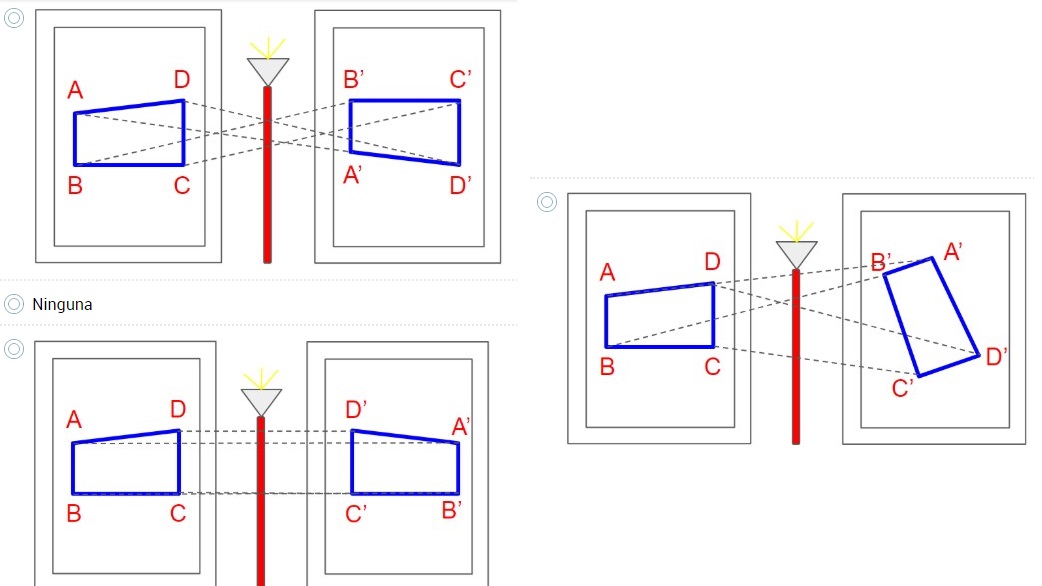
3. Un artista tiene una obra sobre la pared, sin embargo quiere tener la misma obra pero reflejada respecto a una lámpara de piso. ¿Cuál es la opción que representa la simetría axial?
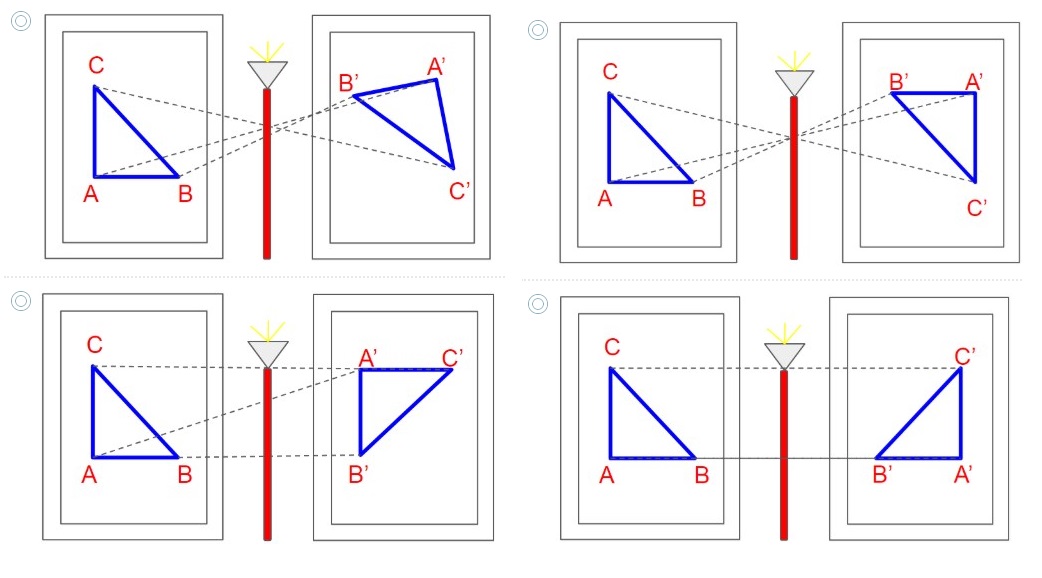
4. Un artista tiene una obra sobre la pared, sin embargo quiere tener la misma obra pero reflejada respecto a una lámpara de piso. ¿Cuál es la opción que representa la simetría axial?
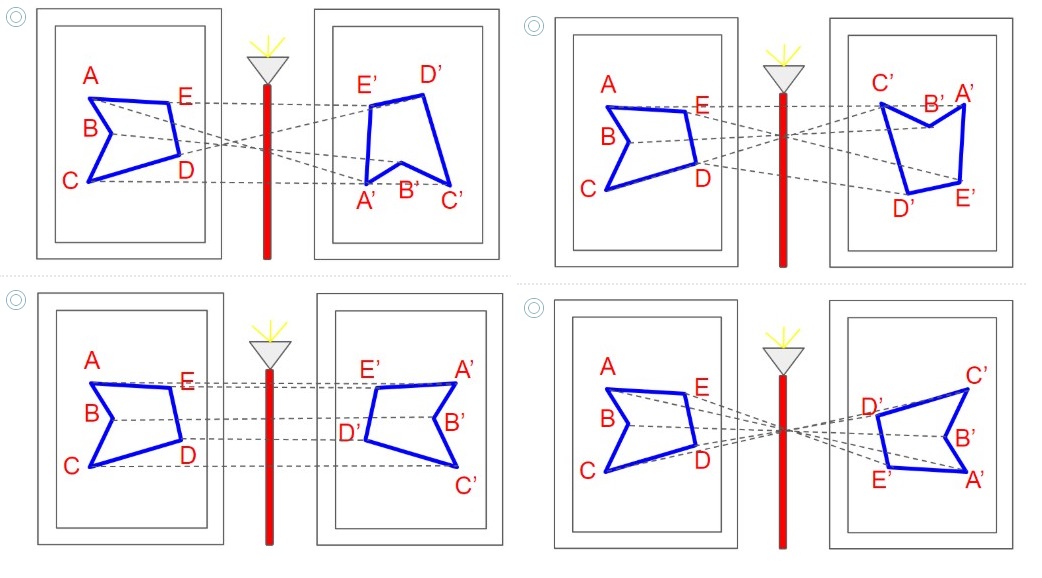
5. Un artista tiene una obra sobre la pared, sin embargo quiere tener la misma obra pero reflejada respecto a una lámpara de piso. ¿Cuál es la opción que representa la simetría axial?
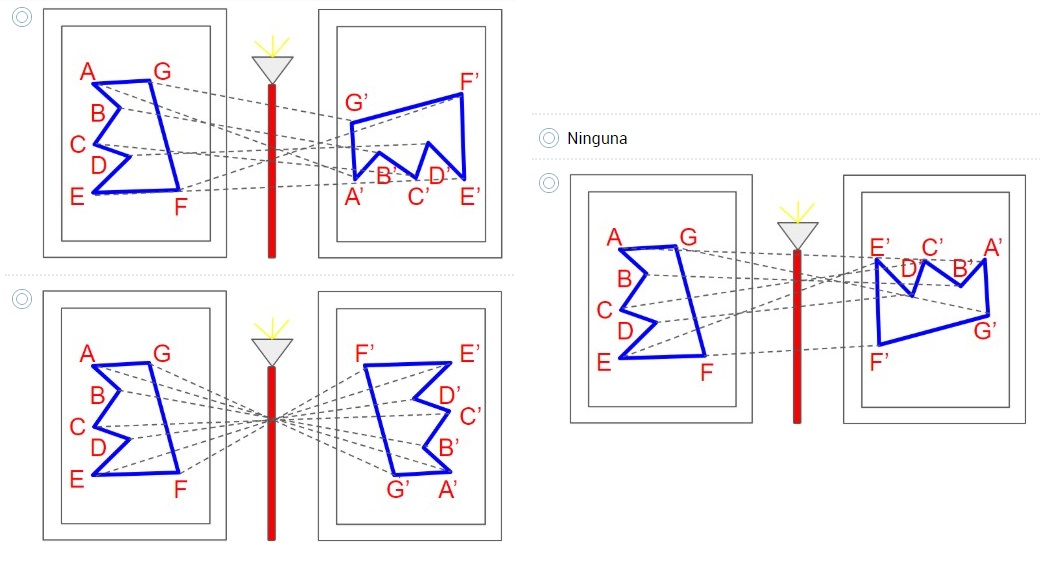
Nota: Si dispones de computador realiza el ejercicio en el siguiente link:
https://pruebat.org/SaberMas/MiClase/inicia/9610/347efda3b4d179433957dc426d73bf98/141216
Ejercicio 6. Simetría Central.
1. Halla en tu cuaderno la figura simétrica de la que te dan respecto al punto C.
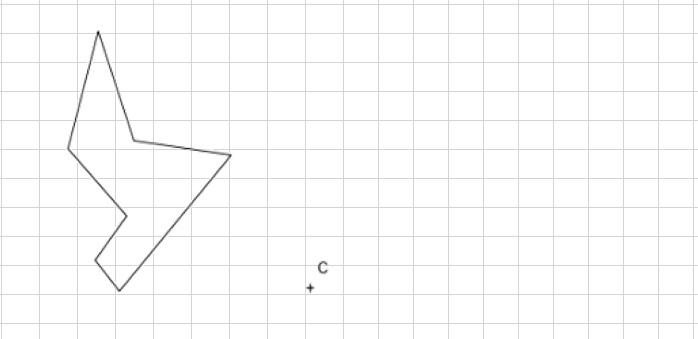
2. Realizar los ejercicios del siguiente enlace: https://www.geogebra.org/m/ad76ffwg
GEOMETRÍA ANALÍTICA BÁSICA
Ecuaciones de líneas rectas
Objetivo de Aprendizaje: Manejar las distintas formas de la ecuación de una recta y también establecer la relación Gráfica – Ecuación, a partir de los parámetros que la rigen. Conectar estos conocimientos con las operaciones hechas en cursos previos, tales como: sistemas de ecuaciones y función afín.
1. PUNTOS COLINEALES DEFINICIÓN:
La relación gráfica de colinealidad fue visto en el primer periodo del grado sexto; en este punto trataremos la fórmula para verificar si entre dos o más puntos existe colinealidad. Esto lo haremos a través de la fórmula de la pendiente.
Sin más entremos en detalles:
FÓRMULA DE LA PENDIENTE:
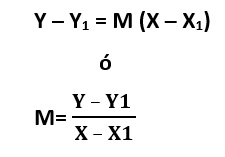
Tres o más puntos de un plano son colineales si pertenecen a una misma línea recta, es decir, si las pendientes entre cada par de puntos tiene el mismo valor.
EJEMPLO: Dados los puntos de coordenadas
P(-1,-3), Q(3,1), R(7,5), determinar si son o no
colineales.
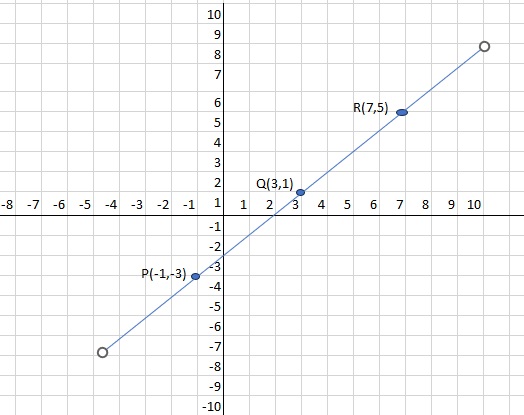
Aunque gráficamente es evidente la colinealidad, no siempre tenemos la opción de dibujarla y debemos darnos a la tarea de hallar la relación de las pendiente entre los puntos, para ello vamos a emplear la fórmula de la siguiente manera:
1. Primero vamos a hallar la pendiente entre los puntos P y Q:
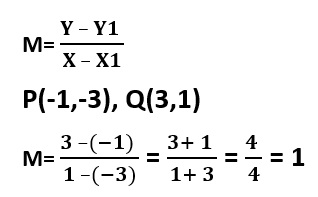
2. Hallamos la pendiente entre los puntos Q y R:
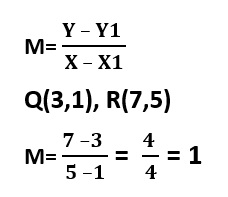
3. Por último hallaremos la pendiente de los puntos P y R:
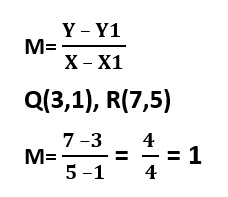
Nos damos cuenta que en todos los puntos nos dió 1, esto significa que existe colinealidad entre todos, es decir, se ubican sobre la misma recta.
2. Ecuación de la recta que pasa por un punto (x1,y1) y tiene una pendiente dada (m)
Para este ejercicio nos deben dar un punto y una pendiente, para emplearemos la fórmula general de la recta
FÓRMULA GENERAL DE LA RECTA:

FÓRMULA DE LA RECTA (PUNTO, PENDIENTE):
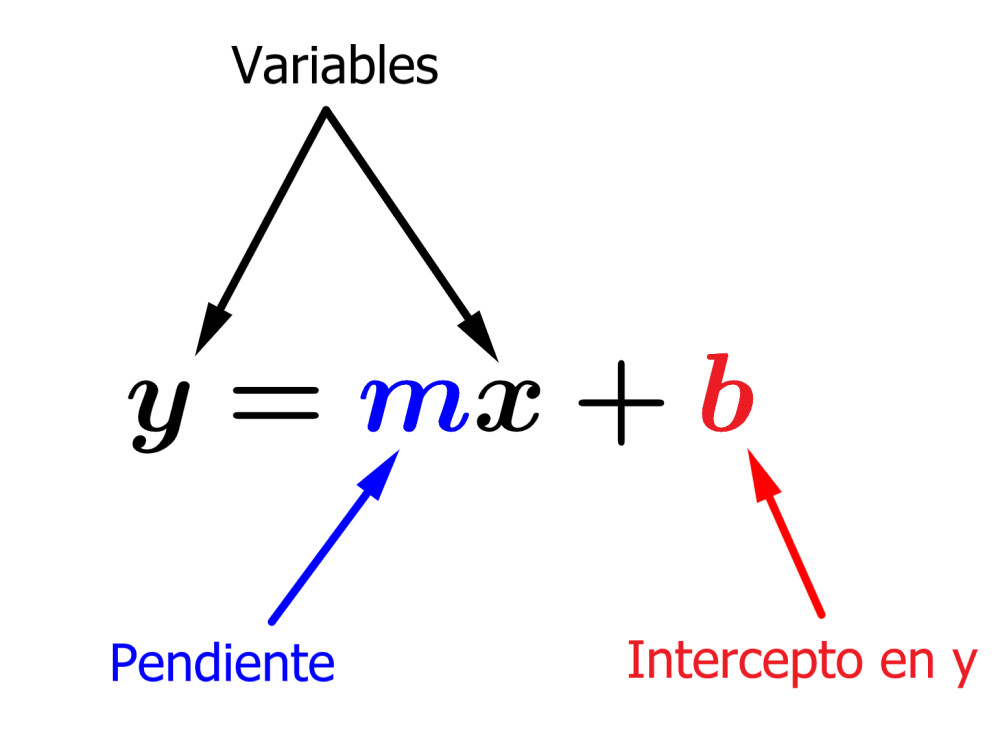
Para entender mejor el tema vamos a desarrollar el siguiente ejemplo:
Ejemplo:
Hallar la ecuación general de la recta que pasa por los puntos (-3,5) y que tiene una pendiente m=-2
1. Iniciaremos empleando y reemplazando en la siguiente fórmula:
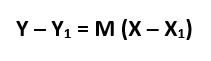

2. Igualamos de tal forma que nos quede la fórmula de la recta
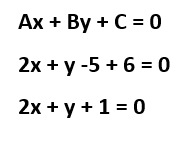
La ecuación de la recta nos dio 2x + y + 1 = 0
Si te quedó dificil comprender el tema, te invitamos a observar los siguientes videos:
Ejercicio 7.
1. Determina en cada caso si los puntos son o no colineales.
1) A(2,3), B(4,5), C(6,7)
2) D(-5,15), E(1,15), F(-4,15)
3) G(5,4), H(14,15), I(9,9)
2. Calcula el valor de p para que los puntos sean colineales.
1) A(4, 6), B(8, p), C(9, 4)
2) R(2p, 5), S(-3,4), T(-1,-2)
3. Hallar la ecuación de la recta que pasa por el punto K(-6, -2) y tiene pendiente M=2/5
Your Title
This is where your text starts. You can click here and start typing. Sed ut perspiciatis unde omnis iste natus error sit voluptatem accusantium doloremque laudantium totam rem aperiam eaque ipsa quae ab illo inventore veritatis et quasi architecto beatae vitae dicta sunt explicabo nemo enim ipsam voluptatem.


