GEOMETRÍA

Grado 9 - Periodo 2

1. Rectas cortadas por paralelas

Recordemos: Para considerar los ángulos generados entre dos paralelas cortados por una secante, es necesario recordar el significado de rectas paralelas y recta secante.

Al trazar dos rectas en un mismo plano, estas rectas pueden ser:

Ahora que sabes que son rectas secantes y paralelas entremos en el tema observando la siguiente imagen:

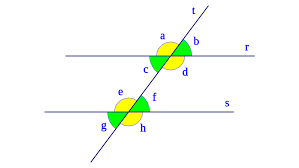
Observa que: Las rectas  r y s  son paralelas y la recta t es secante.

Dos rectas paralelas cortadas por una recta secante forman ocho ángulos, los cuales en la imagen están señalados por letras minúsculas: a, b, c, d, e, f, g, h

Estos, forman diferentes clases de ángulos, que se clasifican de acuerdo a las características que cumplan, de acuerdo a la posición que ocupen respecto a las rectas paralelas y a la recta secante.

Aprende estos conceptos:

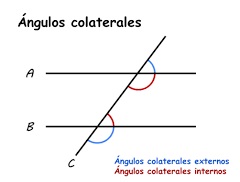
1. Ángulos Colaterales: son aquellos ángulos situados del mismo lado de la secante, existen de dos tipos: Internos y Externos

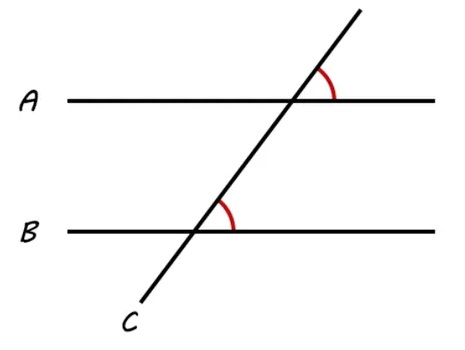
2. Ángulos Correspondientes: son un par de ángulos que podemos encontrar del mismo lado de una transversal que corta dos rectas paralelas. Estos ángulos se encuentran en el mismo nivel respecto a la recta paralela a la cual pertenecen y tienen la misma medida o ángulo.

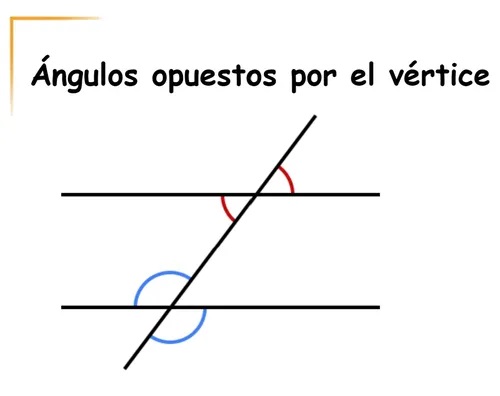
3. Ángulos Opuestos: Los ángulos opuestos por el vértice surgen en el punto de intersección de dos rectas que se cruzan, uno frente al otro, compartiendo el mismo vértice. Los ángulos opuestos por el vértice tienen la misma medida.

Ahora que ya conoces estos conceptos observa todos los ánguos que se forman:

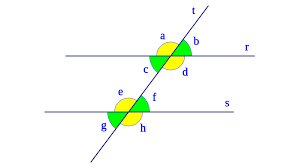
1.Ángulos Colaterales                                        5. Ángulos Alternos Externos

Externos: (a,g)(b,h)                                            (a,h)(b,g)

Internos: (c,e)(d,f)

2.Ángulos Internos                                             6. Ángulos Correspondientes

(c,d,e,f)                                                                (a,e)(b,f)(c,g)(d,h)

3.Ángulos Externos                                            7. Ángulos opuestos por el vértice.

(a,b,g,h)                                                               (a,d)(c,b)(e,h)(f,g)

4.Ángulos Alternos Internos

(c,f)(e,d)

Te invito a observar el siguiente video para que refuerces el tema:

2. Triángulos en posición de Thales

Antes de continuar quiero recordarte que es la Teoría o teorema de Thales, atribuido al matemático griego Tales de Mileto en el siglo VI A.C. 

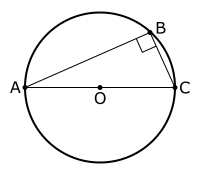
Thales creó dos teoremas el segundo es el que vamos a ver en este capítulo ahora te recordaré el primero, el cual está enfocado a  triángulos rectángulos, las circunferencias y los ángulos inscritos, consiste en el siguiente enunciado:

Sea B un punto de la circunferencia de diámetro AC y centro "O", distinto de A y de C. Entonces, el triángulo ABC es un triángulo rectángulo donde <ABC = 90°. Al rotar el punto B, Siempre formará un triángulo rectángulo.

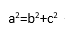
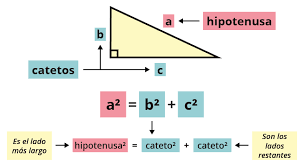
Teorema2: En un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de cada uno de los catetos:  

Observa el siguiente video para reforzar tu conocimiento:

Teorema 1 de Tales:

TRIÁNGULOS EN POSICIÓN DE TALES

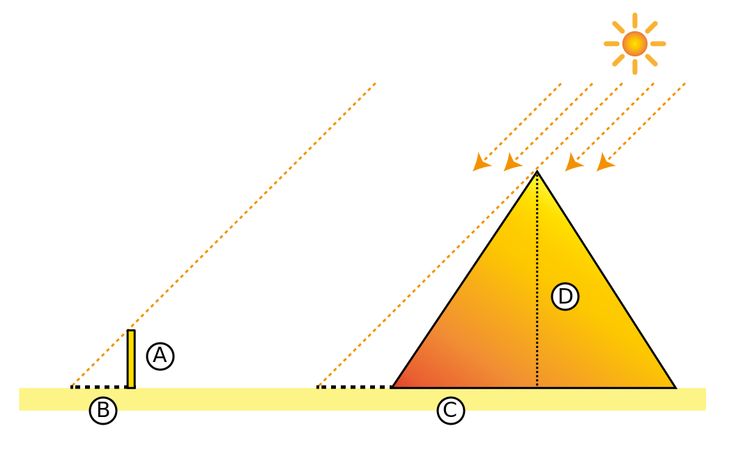
HISTORIA:  Tales de Mileto en un viaje a Egipto, visitó las pirámides de Guiza (conocidas como Keops, Kefrén y Micerinos), construidas varios siglos antes. Admirado ante tan portentosos monumentos de esta civilización, quiso saber su altura. De acuerdo a la leyenda, trató este problema con semejanza de triángulos (y bajo la suposición de que los rayos solares incidentes eran paralelos), pudo establecer una relación de semejanza (teorema primero de Tales) entre dos triángulos rectángulos, por un lado el que tiene por catetos (C y D) a la longitud de la sombra de la pirámide (conocible) y la longitud de su altura (desconocida), y por otro lado, valiéndose de una vara (clavada en el suelo de modo perfectamente vertical) cuyos catetos conocibles (AyB) son, la longitud de la vara y la longitud de su sombra. Realizando las mediciones en una hora del día en que la sombra de la vara sea perpendicular a la base de la cara desde la cual medía la sombra de la pirámide y agregando a su sombra la mitad de la longitud de una de las caras, obtenía la longitud total C de la sombra de la pirámide hasta el centro de esta.

De ahí nacio este teorema conocido como triángulos en posición de Tales:

Se dice que dos triángulos están en posición de Tales si tienen en común un ángulo y los lados opuestos a este ángulo común en cada triángulo son paralelos. Por el teorema de Tales, los lados correspondientes son proporcionales y los dos triángulos por ende son semejantes. 

Ejemplo:

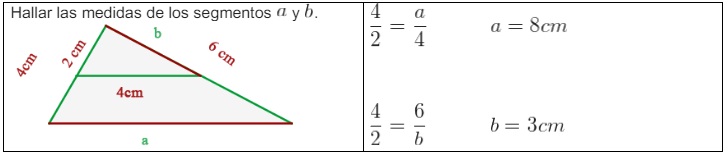
Ejercicios:

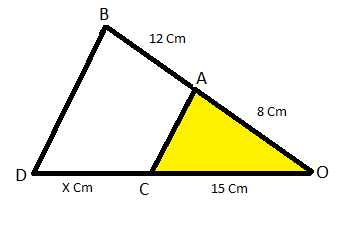
1. Resulve el valor de X:

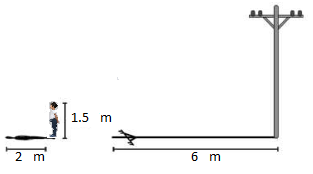
2) Observa la imagen de un poste, un hombre y sus sombras: ¿Cuánto mide la altura del poste? 

A) 4,5 m. B) 6,5 m. C) 8 m. D) 9 m 

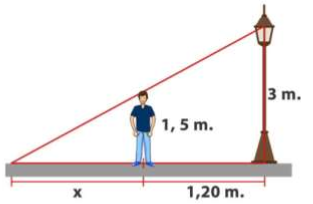
3. Nicolás mide 1,50 m. de altura, se encuentra a 1,20 m. de un poste que tiene encendida su luminaria a 3 m. del suelo, ¿cuál es el largo de la sombra que proyecta Nicolás?

ÁDICIÓN AL TEOREMA DE TALES

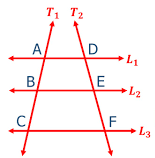
Si tres o más rectas paralelas (L) son cortadas por 2 o más secantes (T), la razón de las longitudes de los segmentos determinados en una de las paralelas es igual a la razón de las longitudes de los segmentos correspondientes determinados por las otras dos paralelas.