Grado 7 - Periodo 3

Matemáticas

TEMA: Proporcionalidad

1. Razones y proporciones, 2. proporcionalidad directa, 3. proporcionalidad inversa, 4. aplicación a la proporcionalidad, 5. regla de tres compuesta

LOGRO. Identifica y utiliza relaciones de proporcionalidad, desarrollando estrategias para representar e interpretar los datos y emplearlas para resolver problemas en situaciones cotidianas, expresando los resultados de forma coherente.

ESTANDAR BÁSICO DE COMPETENCIA: Analizo las propiedades de correlación positiva y negativa entre variables, de variación lineal o de proporcionalidad directa y de proporcionalidad inversa en contextos aritméticos y geométricos.

CONOCIMIENTOS PREVIOS: Regla de tres

1. RAZONES Y PROPORCIONES

1.1. RAZÓN

Una razón es una comparación entre dos cantidades mediante una división. La razón entre a y b se puede escribir como a/b o a : b, con la condición de que b ≠ 0. Se lee " a es a b".

Al calcular el cociente entre el antecedente y el consecuente de una razón se obtiene un número que se conoce como el valor de la razón. Si dos razones tienen el mismo valor se dice que son equivalentes.

Ejemplo:

La razón entre 6 y 5 se escribe

Cómo calculamos una razón?

Calcular una razón, significa determinar el valor de esta, el que se establece haciendo la división entre el antecedente y el consecuente.

Ejem´plo:

Actividad 1:

1. Representa cada razón como una fracción.

2. Escribir la razón pedida en cada uno de los siguientes casos:  En una fábrica trabajan 40 hombres y 25 mujeres encontrar la razón entre

a) El número de hombres y el número de mujeres

b) El número de hombres y el total de trabajadores

c) El número de mujeres y el total de trabajadores

3) Escribir la razón que corresponde a cada una de las siguientes expresiones:

4. A los alumnos de 6º básico del colegio se les consultó acerca del lugar que preferían para pasar sus vacaciones. Las respuestas son las siguientes:

Utilizando los resultados de esta encuesta y expresa la razón de dos formas distintas:

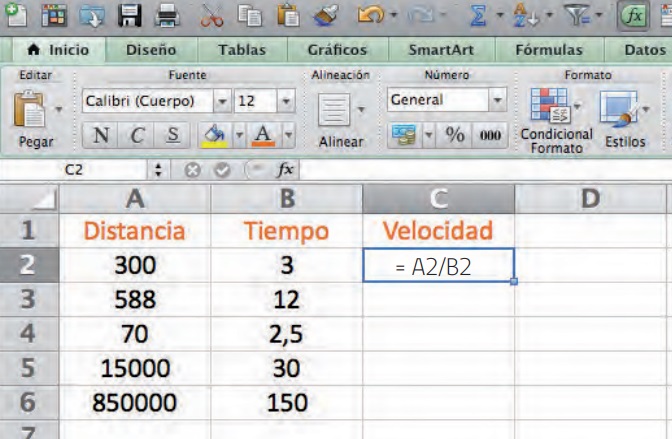
5. Desarrolla en Excel la siguiente proporcionalidad con sus fórmulas

1.2. PROPORCIÓN

Una proporción es la relación directa o inversa que existe entre dos variables, es decir, que dos variables son afectadas si una de ellas cambia.

Por ejemplo: Variable tamaño versus variable Ingredientes: Mientras más grande es la torta se entiende que usa más ingredientes.

Como podemos ver, si la variable "cantidad de huevos" sube, la otra variable "valor del huevo" también sube. Y se dice que es directamente proporcional.

1.2.1 Proporcionalidad Directa

Podemos definir una proporción directa como dos variables directamente relacionadas, es decir, si una variable aumenta la otra variable también aumenta. Si una variable disminuye la otra variable también disminuye. También se conoce una variable como independiente y la otra variable como dependiente.

Ejemplo: Variable cantidad de huevos versus variable valor del huevo.

Para calcular proporciones directas usamos la regla de tres.

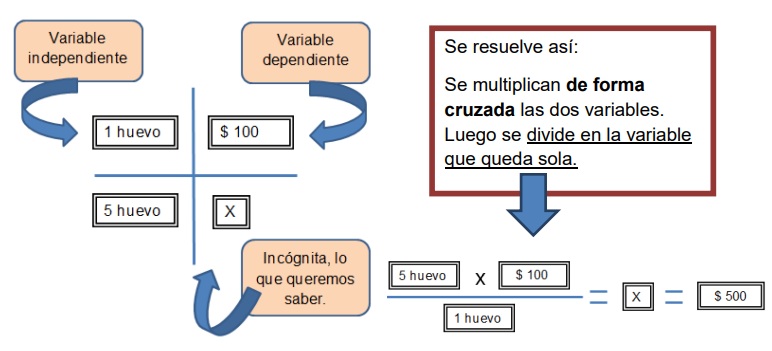
Ejemplo: Si 1 huevo cuesta $100, ¿Cuánto cuestan 5 huevos?

Actividad 2:

Calcula las siguientes proporciones directas usando la regla de tres:

a) La señora Juanita cocina tortas, si con 10 huevos ella cocina 1 tarta, ¿Cuántas tortas puede cocinar con 40 huevos?

b) Un automóvil recorre 200 kilómetros con 30 litros de bencina. ¿Cuántos kilómetros puede recorrer con 75 litros de bencina?

c) Francisco gana $5.000 por repartir 1.000 volantes. ¿Cuántos volantes debe repartir para ganar $65.000?

Para calcular proporciones INVERSAS usamos también la regla de tres.

1.2.2. Proporcionalidad inversa

Podemos definir una proporción inversa como dos variables inversamente relacionadas, es decir, si una variable aumenta la otra variable disminuyen o si una variable disminuye la otra variable aumenta.

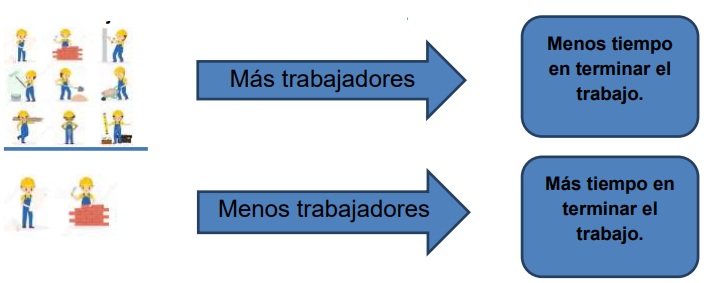
Ejemplo de proporción inversa: variable cantidad de trabajadores versus el tiempo que se demoran en realizar el trabajo. Es decir, si un trabajo lo hacen más trabajadores se demoran menos en terminar, o si son menos trabajadores se demoran más en terminar.

Ejemplo: Si 10 trabajadores se demoran 6 días en hacer un trabajo, ¿cuánto se demoran 20 trabajadores?

Actividad 3:

Calcula las siguientes proporciones inversas usando la regla de tres.

a) Si 20 trabajadores se demoran 100 días en terminar de pavimentar una calle. ¿Cuántos días se demoran en pavimentar la misma calle solo 5 trabajadores?

b) Un automóvil viaja a 100 kilómetros por hora y se demora 4 horas en llegar a su destino, ¿Cuánto se demora si aumenta la velocidad a 120 kilómetros por hora?

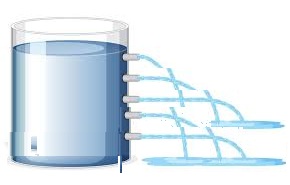
c) Una llave de agua llena una piscina en 15 horas, ¿Cuánto se demoran en llenar la misma piscina 5 llaves de agua?

2. REGLA DE TRES COMPUESTA

La diferencia de la regla de 3 simple con la regla de 3 compuesta es que en la primera se relacionan dos magnitudes y en la segunda se relacionan tres o más magnitudes. Aunque en este post solo resolveremos problemas con 3 magnitudes, la forma de resolver los problemas con más magnitudes es la misma.

2.1. Ejemplo de regla de 3 compuesta con las dos proporcionalidades directas

Hemos ido a la fuente del pueblo para recoger agua. Sabemos que 5 botellas de agua, de 2 litros cada una, pesan 10 kilos. ¿Cuánto pesan 2 botellas de 3 litros cada una?

Las tres magnitudes que tenemos en el problema son: botellas, litros y kilos. Escribimos la relación entre ellas sabiendo que:

5 botellas, 2 litros, 10 kilos

2 botellas, 3 litros, X kilos

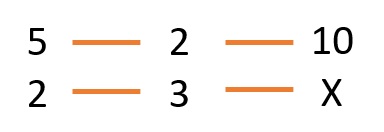
Ahora tenemos que averiguar la relación entre las magnitudes, comparando siempre con la magnitud donde esté la incógnita X.

Comparamos botellas con kilos: Si hay menos botellas entonces pesarán menos. Tienen proporcionalidad directa.

Comparamos litros con kilos: Si hay más litros entonces pesarán más. Tienen proporcionalidad directa.

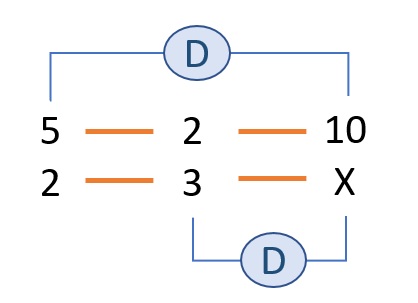
Ahora, escribimos las relaciones en forma de fracción para poder despejar la incógnita X. La primera fracción es donde está la incógnita (esto no es obligatorio, pero ayuda para después resolverlo). Después, igualamos a la multiplicación de las dos fracciones:

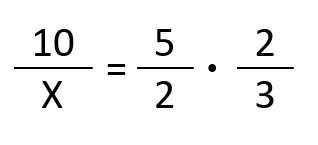
Y resolvemos:

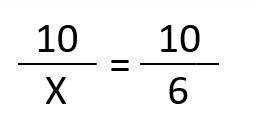
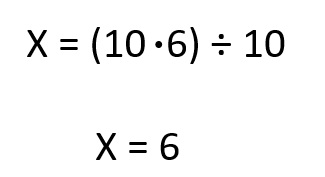
Podemos despejar la X haciendo los productos cruzados:

2 botellas, de 3 litros cada una, pesan 6 kilos.

2.2. Ejemplo de regla de 3 compuesta con una proporcionalidad directa y otra inversa

En 4 días, 6 impresoras han impreso 100 libros. ¿Cuántos días tardarán en imprimir 50 libros si tenemos 4 impresoras?

Las magnitudes que tenemos en el problema son: días, impresoras y libros. La relación entre ellas es:

4 días, 6 impresoras, 100 libros.

X días, 4 impresoras, 50 libros.

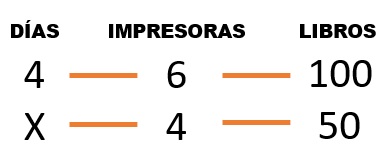
Vemos la proporcionalidad entre las magnitudes:

Si hay que hacer menos libros entonces se necesitan menos días. Proporcionalidad directa.

Si hay menos impresoras entonces se necesitan más días. Proporcionalidad inversa.

Ahora, escribimos las relaciones en forma de fracción para poder despejar la incógnita X. ¡OJO! La magnitud que es inversa debemos invertirla, es decir, el denominador pasa a ser numerador y el numerador pasa a ser denominador.

Despejamos X:

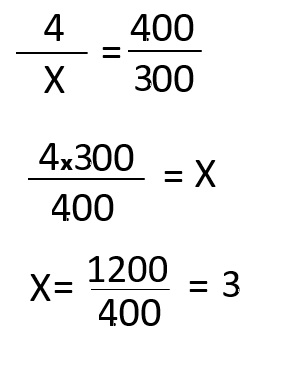
Otra forma de resolverlo es por el método de los productos cruzados:

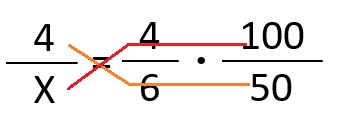
En mi concepto es mejor que te aprendas este método por que pueden haber más de 3 fraccionarios

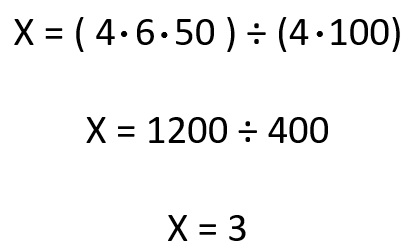
Para imprimir 50 libros, 4 impresoras tardan 3 días.

2.3. Ejemplo de regla de 3 compuesta por dos proporcionalidades inversas

En un albergue hay 180 cachorros que comen 4 porciones de alimento diario por 10 días. Próximamente serán 200 cachorros y solo se les dará 3 porciones díarias. Si se cuenta con la misma cantidad de alimento, ¿Cúantos días les durará?

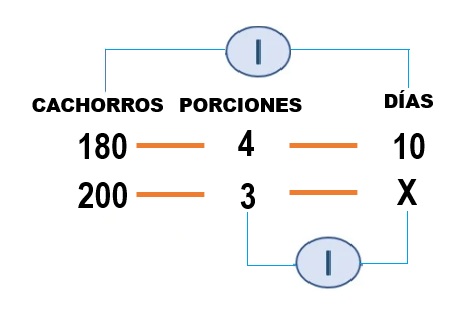
Las magnitudes que tenemos en el problema son: cachorros, porciones y días. La relación entre ellas es:

180 cachorros, 4 porciones, 10 días.

200 cachorros, 3 porciones, X días.

Vemos la proporcionalidad entre las magnitudes:

Si hay más cachorros para comer, la comida durará menos días. Proporcionalidad inversa.

Si hay menos porciones de comida durará más días. Proporcionalidad inversa.

Ahora, escribimos las relaciones en forma de fracción para poder despejar la incógnita X. ¡OJO! La magnitud que es inversa debemos invertirla, es decir, el denominador pasa a ser numerador y el numerador pasa a ser denominador. En este caso invertimos ambas fracciones.

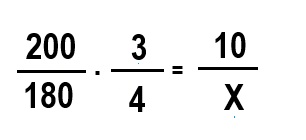
Ahora desarrollamos el ejercicio por cualquiera de los dos métodos ya vistos:

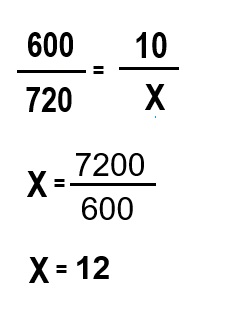
200 cachorros consumiendo 3 porciones díarias les dura la comida 12 días

Si no te quedó claro el tema te invito a observar el siguiente video con proporcionalidad directa:

Proporcionalidad inversa:

Actividad 4:

Desarrolla los siguientes ejercicios en el cuaderno:

1.- 6 máquinas excavadoras hacen una zanja en 18 días, si se averían 2 excavadoras, ¿Cuánto tardarán en abrir la zanja

2.- Un coche que va a 72 Km/h, tarda 3h y 15 minutos en hacer un recorrido.¿Cuánto tardará otro coche en hacer el mismo recorrido si va a 90 km/h?

3.- Si 3 libros de lectura cuestan 36 €, ¿Cuánto costarán 2 docenas de libros?

4.- Si 5 fotocopias cuestan 40 céntimos, ¿cuántas fotocopias haré con 8 €?

5.- Un depósito lleno de agua tarda 24 minutos en vaciarse abriendo 5 desagües. Si queremos que se vacíe en 15 minutos ¿Cuántos desagües hay que abrir?

ACÁ PUEDES DESCARGAR LA GUÍA