Grado 7 - Periodo 2

Matemáticas

TEORIA DE NÚMEROS NUMEROS FRACCIONARIOS

1. Definición del conjunto de los números racionales, 2. Fracciones equivalentes, 3. Simplificación-complicación de fracciones, 4. Clasificación de racionales, 5. Orden de los números racionales, 6. Representación de los números racionales en la recta numérica.

DBA 3. Utilice diferentes relaciones, operaciones y representaciones en los números racionales para argumentar y solucionar problemas en los que aparecen cantidades desconocidas.

Comprende y resuelve problemas, que involucran los números racionales con las operaciones (suma, resta, multiplicación, división, potenciación, radicación)

ESTANDAR BÁSICO DE COMPETENCIA: Utilizo números racionales, en sus distintas expresiones. (fracciones, razones, decimales o porcentajes) para resolver problemas en contextos de medida.

Reconozco y generalizo propiedades de las relaciones entre números racionales (simétrica, transitiva, etc.) y de las operaciones entre ellos (conmutativa, asociativa, etc.) en diferentes contextos.

Saberes anteriores: Manejo de operaciones con fraccionarios, mínimo común múltiplo. Te invitamos a observar los siguientes video, para que recuerdes estos temas de periodos pasados:

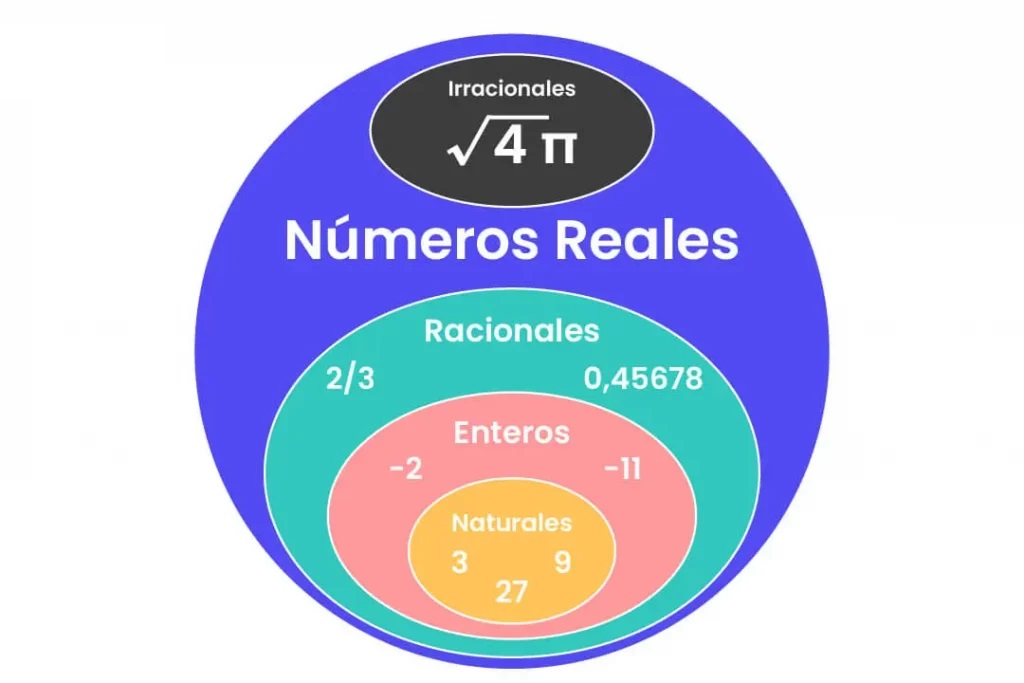
1. DEFINICIÓN DEL CONJUNTO DE LOS NÚMEROS RACIONALES

Un número racional es un número que se expresa en la forma p/q donde p y q son enteros y q es distinto de cero.

En resumen, un número racional es:

Fraccionario: Puede ser expresado como una fracción, con numerador y denominador enteros.
Números enteros:
Decimal finito o periódico: Su forma decimal termina o se repite en un patrón.
Irracional: Tienen decimales infinitos no periódicos. Ej: El número π= 3.14159 26535 89793 23846 26433...

En este periodo nos centraremos en algunos tipos de fracciones que no hemos visto y en decimales infinitos periódicos y no periódicos.

2. FRACCIONES EQUIVALENTES

Fracciones equivalentes son las que representan la misma cantidad. Dos fracciones son equivalentes si se cumple que: a/b = c/d qué es lo mismo que: a x d = b x c

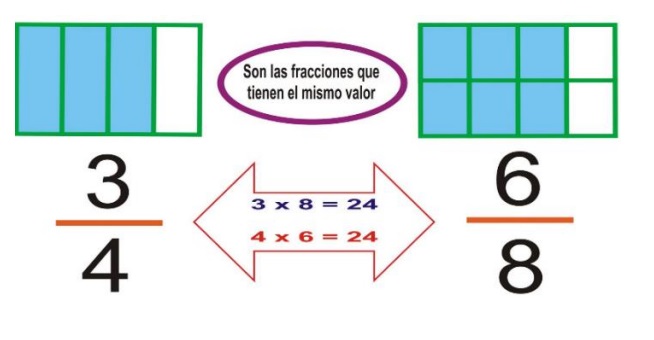
Ejemplo:

Actividad 1:

Escribe en tu cuaderno si las siguientes fracciones son o no equivalentes (Demuéstralo):

3. SIMPLIFICACIÓN/COMPLICACIÓN(Amplificación) DE FRACCIONES

3.1. SIMPLIFICACIÓN:

Para SIMPLIFICAR fracciones se DIVIDE el numerador y el denominador por el mismo número, hasta encontrar la fracción irreducible.

Ejemplo1:

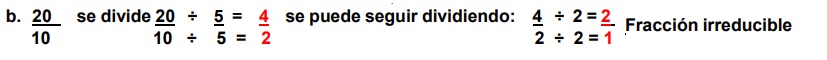
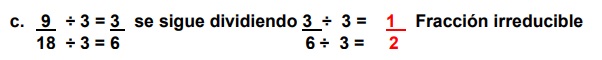
Fracción irreducible: Una fracción que no puede ser simplificada más, porque el numerador y el denominador no comparten divisores comunes además de 1.

Ejemplo 2:

Encontrar las fracciones equivalentes utilizando la simplificación:

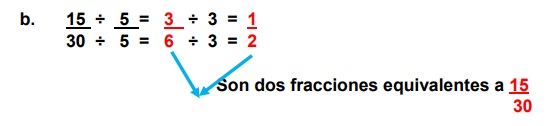
3.2. AMPLIFICACIÓN:

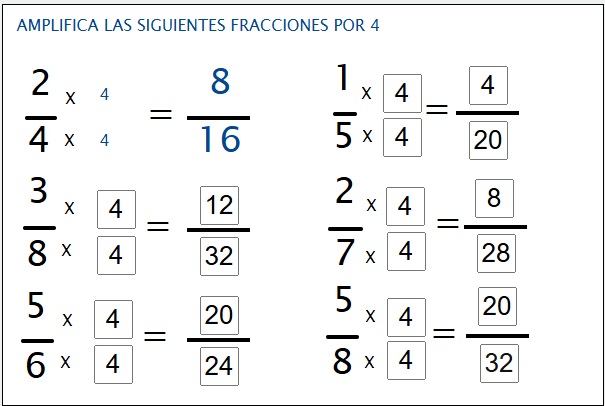
Para AMPLIFICAR una fracción se multiplica tanto el numerador como el denominador por UN mismo número, que sea distinto de cero.

Ejemplo1:

Ejemplo2:

Para reforzar el tema, te invito a observar el siguiente video:

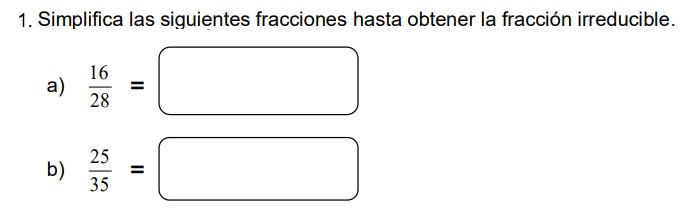
Actividad 2: Simplificación y amplificación (Contesta en tu cuaderno)

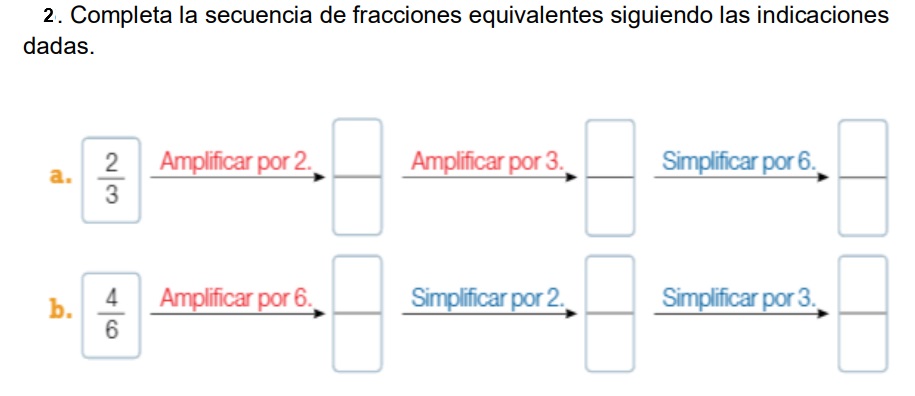
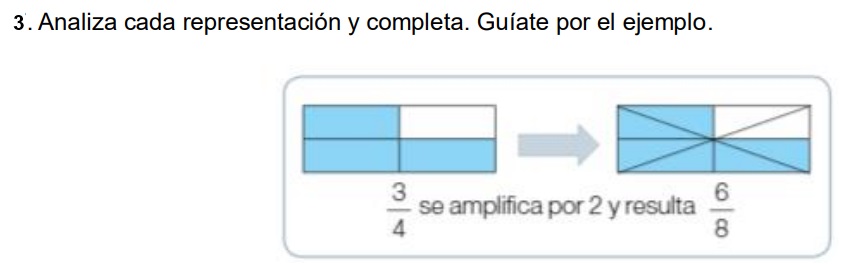
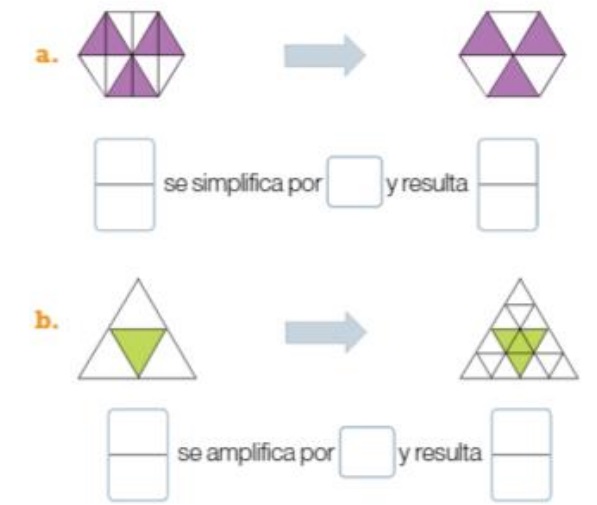
4. CLASIFICACIÓN DE NÚMEROS RACIONALES

En el grado 6, segundo periodo vimos algunas de ellas que son:

Fracciones Propias: El numerador es menor que el denominador. Representan un valor menor a la unidad (por ejemplo, 2/5, 3/7).
Fracciones Impropias: El numerador es mayor o igual que el denominador. Representan un valor igual o mayor a la unidad (por ejemplo, 5/2, 7/3, 4/4).
Fracciones Mixtas: Se componen de una parte entera y una fracción propia (por Ej: 2 1/2, 3 1/4).
Fracciones Equivalentes: Representan la misma cantidad, aunque tengan diferente numerador y denominador (por ejemplo, 1/2 y 2/4).
Fracciones Homogéneas: Tienen el mismo denominador (por ejemplo, 2/5 y 3/5).
Fracciones Heterogéneas: Tienen diferentes denominadores (por ejemplo, 2/5 y 3/7).
Fracciones Unitarias: Son fracciones propias con numerador 1 (por ejemplo, 1/2, 1/3, 1/4).

Como dijimos en un inicio, los números racionales se dividen en fraccionarios, decimales finitos, infinitos y estos a su vez en periódicos, semiperiódicos e irracionales.

En este apartado nos encargaremos de la explicación de los decimales finitos e infinitos.

DECIMALES

Un número decimal es aquel que no es entero, es decir tiene una parte que es menor que la unidad (1,2,3,4,5....), consta de una parte entera y una parte decimal, separadas por una coma (o punto, dependiendo del idioma). La parte decimal representa fracciones de la unidad. Ej:

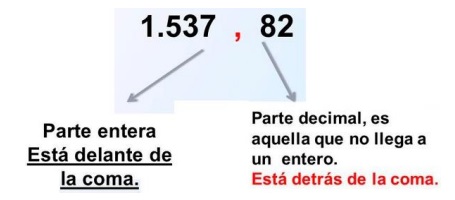
Existen dos tipos de números decimales, estos son los decimales finitos y los infinitos, los decimales infinitos a su vez de dividen en periódicos, semiperiódicos y no periódicos o irracionales.

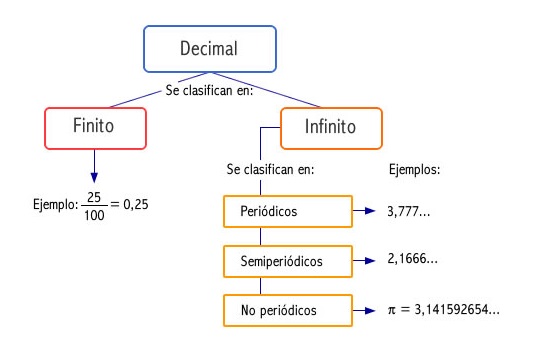
4.1. Decimales finitos

Un número decimal exacto o finito es el que se obtiene de una fracción que tiene en el denominador una potencia de 10 o una simplificación de ellas, también podemos decir que es un número decimal que tiene fin.

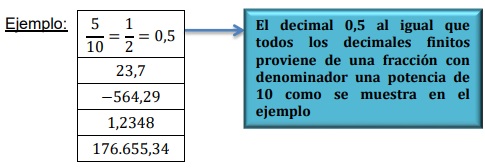
4.2. Decimales infinitos

Son aquellos números que no se acaban, es decir, hay uno o varios números que se repiten infinitamente. Por ejemplo: 3,333333..... es infinito por que el 3 se repite indefinidamente. Cuando el cociente (División) se repite indefinidamente hablamos de un número decimal infinito y la parte en que se repite la identificamos como período.

4.2.1. Infinito Periódico

Un decimal infinito es periódico, si su período comienza inmediatamente después de la coma.

4.2.2. Infinito SemiPeriódico

Un decimal infinito es semiperíodo si el período no empieza inmediatamente después de la coma.

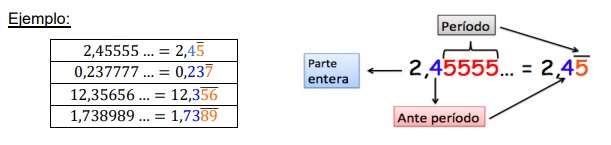
4.2.3. Infinito Irracionales o no periódico

En su forma decimal, tienen infinitas cifras que no siguen un patrón repetitivo (no son periódicos)

Un número irracional es un número que no se puede escribir en fracción - el decimal sigue para siempre sin repetirse. Los decimales no siguen ningún patrón, y no se puede escribir ninguna fracción que tenga el valor Pi. Números como 22/7 = 3.1428571428571... se acercan pero no son correctos.

Para comprender mejor el tema, te invitamos a observar el siguiente video:

Actividad 3:

Responde en el cuaderno

Identifica que tipo de decimal son los siguientes números (observa el ejemplo).

CONVERSIÓN DE NÚMEROS DECIMALES A FRACCIONARIOS

1. Decimales infinitos periódicos:

a. Cuando la parte entera es un cero:

Pondremos en el numerador los números de los decimales sin la coma, y en el denominador un 9 por cada número que tengamos en los decimales Veamos unos ejemplos:

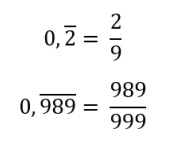
b. Cuando la parte entera no es un cero:

Pondremos en el numerador todos los números sin la coma, tanto los números enteros como los números decimales, y le restamos los números enteros, o dicho de otra manera, los números que están antes de la coma. En el denominador un 9 por cada número que tengamos en los decimales al igual que hicimos antes. Veamos unos ejemplos:

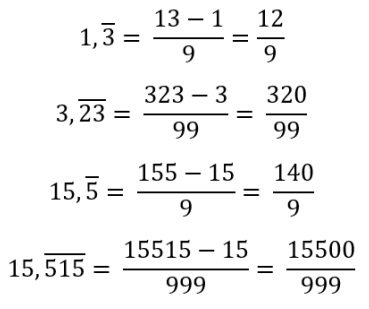
Te invitamos a observar el siguiente video:

2. Decimales infinitos periódicos mixtos:

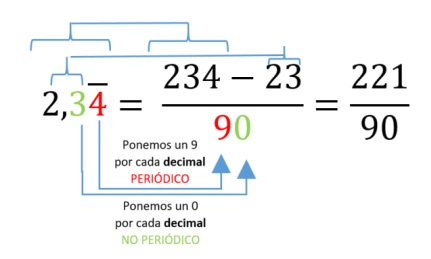
En este caso, en el numerador pondremos el número sin comas, tanto si tiene parte entera como decimal.

A continuación restaremos el número que esté fuera del periodo sin poner comas. En el ejemplo de abajo vemos que el 2 y el 3 están fuera del periodo, ya que solo tenemos al 4 en el periodo. En el denominador empezaremos colocando un 9 por cada decimal periódico que tengamos. En el ejemplo de abajo solo está el 4 en el periodo, por lo que ponemos un 9. Si la parte periódica fuera, por ejemplo 41, pondríamos dos 9. Luego, tras poner los 9 pondremos un 0 por cada decimal que esté antes del periodo (importante el detalle: por cada DECIMAL, por cada número que está a la derecha de la coma antes del periodo. No ponemos 0 por los números enteros que hay antes de la coma).

Te invitamos a observar el siguiente video:

3. Decimal finito

Escribe el número decimal sin la coma como numerador y, en el denominador, escribe un 1 seguido de tantos ceros como cifras decimales tenga el número. Luego, simplifica la fracción si es posible.

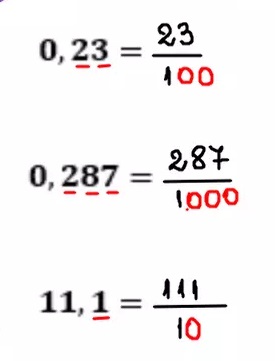
NOTA: Un número decimal irracional, por definición, no se puede expresar como una fracción de enteros, ya que su representación decimal es infinita y no periódica.

Actividad 4: Conversión - Contesta en el cuaderno:

1. transformar los siguientes números decimales finitos en fracciones

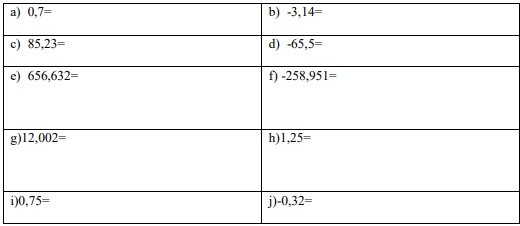
2. Transformar los siguientes números decimales periódicos en fracciones

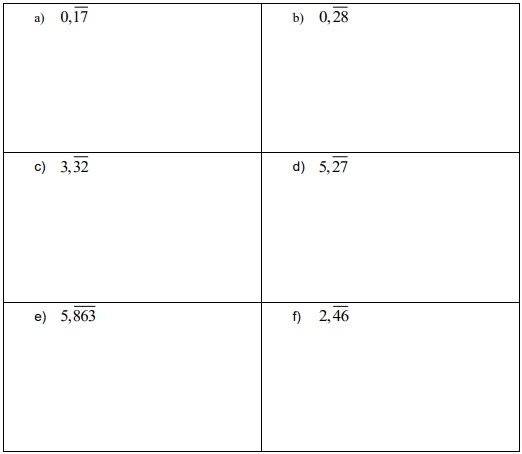
3. Transformar los siguientes números decimales semiperiódicos en fracciones

5. ORDEN DE LOS RACIONALES

Los números racionales son aquellos que se pueden escribir como una razón. El conjunto de los números racionales se denota con la letra ℚ. Todo racional expresa una o varias partes iguales de la unidad. Además, en toda fracción existen dos términos: "𝑎" llamado numerador y "𝑏" llamado denominador. Es decir:

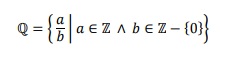
Nota: En grado 6, en el segundo periodo vimos todo lo relacionado con fracciones, tipo de fracciones y operaciones, ahora vamos a ver otros tipos de racionales.

ORDEN EN LOS RACIONALES

Los números racionales representan cantidades, por lo tanto unos pueden representar más y otros menos, es decir hay una relación de orden entre ellos.

Es por eso, que podemos determinar cuando un número es mayor que otro o si son iguales.

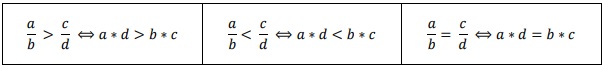
Ejemplo 1:

Además, unos conjunto de racionales se pueden ordenar, de menor a mayor o viceversa, de la siguiente forma:

1. Calcular el MCM de los denominadores.

2. Amplificar cada fracción para que todas tengan igual denominador.

3. Ordenar de menor a mayor o viceversa.

Ejemplo 2:

Ordena de menor a mayor las siguientes fracciones:

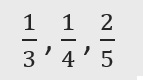
1. Calcular el mínimo común múltiplo de los denominadores. 𝑀𝐶𝑀(3, 4, 5) = 60.

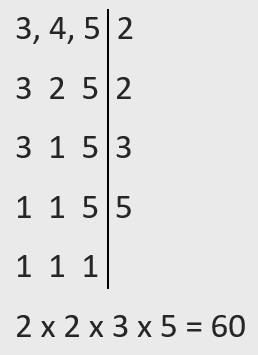
2. Amplificar las fracciones para que tengan el mismo denominador.

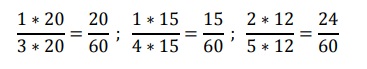
3. Escribir las fracciones ordenadas.

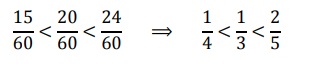
Te invito a observar el siguiente video para reforzar el tema:

NOTA: Este ejercicio también nos sirve para hallar varias fracciones en medio de 2. Se puede intercalar infinitos racionales entre dos racionales distintos, ya que el conjunto ℚ es denso, por no decir infinito.

Ejemplo 3:

Intercalar 3 fracciones entre:

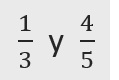
1. Calcular el mínimo común múltiplo de los denominadores.

𝑀𝐶𝑀(3, 5) = 15

2. Amplificar las fracciones.

3. Escribir las fracciones intercaladas.

Actividad 5: Orden en los racionales

Responde en el cuaderno:

1. Coloca en el ( ) el signo > , < o = según corresponda

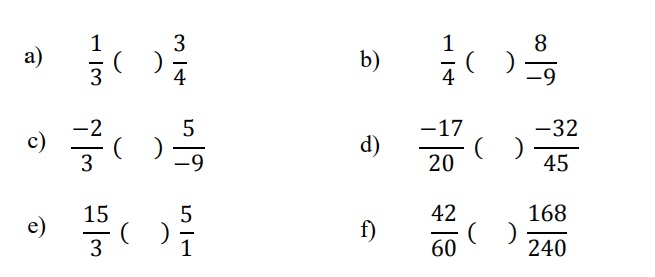
2. Ordena de menor a mayor los siguientes racionales:

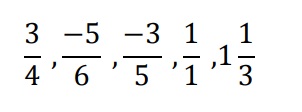
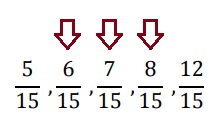
3. Intercala 5 racionales entre:

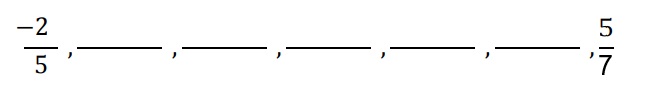
6. REPRESENTACIÓN DE LOS NÚMEROS RACIONALES EN LA RECTA NUMÉRICA

Vamos a comenzar este tema mediante ejemplos para su mayor comprensión.

Ejemplo1. En la siguiente figura se observa el peso de cinco bultos

¿Cómo podría representarse en la recta numérica el peso de cada bulto?

1. Para representar el peso de cada bulto en la recta numérica, primero se debe expresar cada peso en fracciones con el mismo denominador (como en el tema pasado, orden en los racionales), en el cual no vamos a realizar su procedimiento por ser un tema visto.

2. Ordenamos

Observa la respuesta:

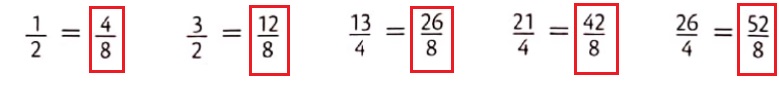
3. Posteriormente, se divide cada unidad de la recta según lo que indica el denominador (ocho partes iguales) y se toman tantas partes como indique el numerador (Contando cada una desde cero). La representación de los pesos en la recta numérica se observa en la siguiente figura

Observa lo que acabamos de hacer en la explicación del siguiente video:

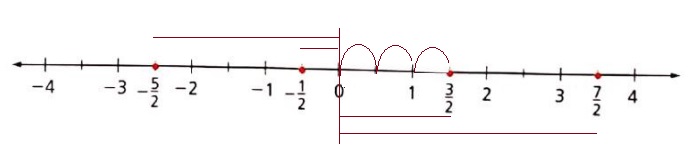
Ejemplo 2: Si se divide en dos partes iguales cada segmento unidad en la recta numérica, se pueden representar los números racionales cuya representación fraccionaria tenga como denominador 2. En la recta numérica de la siguiente figura se observa la representación de los números racionales

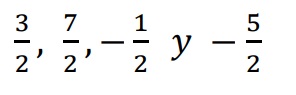
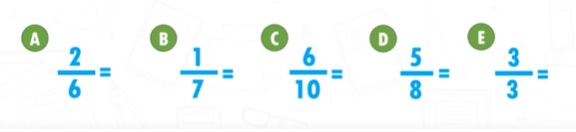
Actividad 6:

Ubica las siguientes fracciones en la recta numérica que aparecen en el video (utilizando el método del m.c.m)

HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:

• Saber Hacer (50%):

a. Elaboración y entrega de las actividades propuestas.

b. Ejercicios de Prueba.

• Saber (25%):

a. Prueba Bimestral

• Ser - Convivir (25%):

a. Normas de Convivencia.

b. Responsabilidad y Cumplimiento en la entrega de trabajos.

c. Seguimiento a las instrucciones dadas por el docente.

d. Autoevaluación y Coevaluación.

AUTOEVALUACIÓN Y COEVALUACION:

Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:

https://docs.google.com/forms/d/e/1FAIpQLSe8K6emBxx7juVipbyPzTOGq_10Rg7a2XDDfxaaipio4DKZTA/viewform?usp=pp_url