Grado 7 - Periodo 2
Estadística

TEMAS:
Medidas de dispersión
1. Rango, 2. Desviación media, 3. Varianza y 4. desviación estándar (introducción).
OBJETIVO: Cuantificar la variabilidad de un conjunto de datos. Esto se logra a través de fórmulas matemáticas que dan un valor numérico.
LOGRO:
Interpretar información estadística presentada en diversas fuentes de información, la analiza y la usa para plantear y resolver preguntas que sean de su interés.
Plantear preguntas para realizar estudios estadísticos en los que representa información mediante histogramas, polígonos de frecuencia, gráficos de línea entre otros; identifica variaciones, relaciones o tendencias para dar respuesta a las preguntas planteadas.
Conocimientos previos: Media, valor absoluto
Recuerda que la media se calcula sumando todos los valores de un conjunto de datos y dividiendo el resultado entre el número de valores. Para recordar te invito a observar el siguiente video:
El valor absoluto: El valor absoluto de un número entero es el número natural que resulta al suprimir su signo. El valor absoluto lo escribiremos entre barras verticales |-5|=5.
Te invito a observar el siguiente video sobre valor absoluto:
MEDIDAS DE DISPERSIÓN
También llamadas medidas de variabilidad, muestran la variabilidad de una distribución, indicando por medio de un número si las diferentes puntuaciones de una variable están muy alejadas de la media. Cuanto mayor sea ese valor, mayor será la variabilidad, y cuanto menor sea, más homogénea será a la media. Así se sabe si todos los casos son parecidos o varían mucho entre ellos. Las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución.
La Dispersión hace referencia a la forma en que se dispersan o alejan las puntuaciones de una distribución o lista de puntajes
Tipos de medida de dispersión
1. Medidas de dispersión absoluta (Rango, Desviación media, Varianza y desviación estándar).
2. Medidas de dispersión relativa (Coeficiente de variación)
1. RANGO
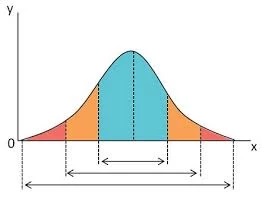
Es la diferencia numérica entre el valor máximo y el valor mínimo; por ello, comparte unidades con los datos. Permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, aún más dispersos están los datos. El rango, también es llamado amplitud o recorrido de medida.
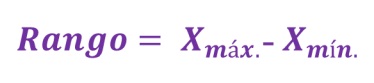
Ejemplo:
Supongamos que deseamos calcular el rango de las edades de un equipo de fútbol.

El jugador más mayor (máximo del conjunto) tiene 31 años, mientras que el más joven (mínimo) 18. Por lo tanto el rango es:
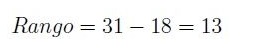
Caracerísticas del rango:
- Solo suministra información de los extremos de la variable
- Informa la distancia entre mínimo y máximo (valor observado)
- Se limita su uso a una información inicial
Te invito a observar el siguiente video sobre rango:
ACTIVIDAD 1:
Contesta en tu cuaderno:
1. Calcular el Rango del siguiente conjunto de datos = 2, 4, 5, 6, 9.
2. Calcular el Rango del siguiente conjunto de datos:
I. {𝟏𝟐, 𝟓, 𝟔, 𝟏𝟒, 𝟖, 𝟏𝟎} el rango es =
II. {𝟏. 𝟐, 𝟏. 𝟓 , 𝟐. 𝟔 , 𝟏. 𝟏𝟒, 𝟐. 𝟔𝟖, 𝟏. 𝟎𝟕 , 𝟏. 𝟏𝟕} el rango es =
3. Las ganancias de un vendedor ambulante durante las cinco primeras semanas del año se presentan en la siguiente tabla:
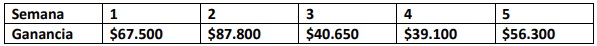
Calcular el rango de sus ganancias
2. DESVIACIÓN MEDIA
La desviación media es una medida que se utiliza para entender qué tanto se alejan los datos de un conjunto promedio.
La desviación es una herramienta fundamental para analizar y comprender conjuntos de datos en diversas disciplinas, como la economía, la psicología, la medicina y muchas otras.
Comprender cómo calcular y utilizarla es crucial para poder hacer afirmaciones precisas y tomar decisiones basadas en datos.
Es una medida que nos ayuda a entender cuánto varían los datos de un conjunto promedio. Si la desviación es grande, significa que los datos están muy dispersos o variados, mientras que si es pequeña, significa que los datos están muy cercanos entre sí.
Su fórmula es:
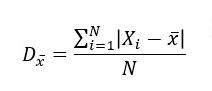
Donde:
Σ = Suma de los términos
| Xi – X | = Valor absoluto de la diferencia entre cada dato y la media
X = Media del conjunto de datos
N = Número de datos en el conjunto

Ejemplo:
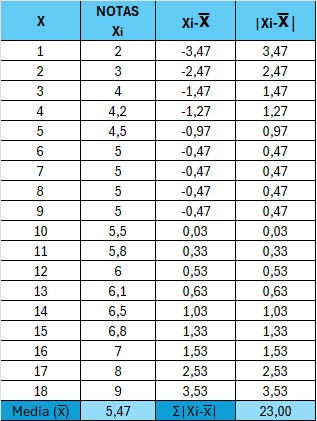
Medir la desviación media de las notas de una clase de 18 alumnos.
En el paso 1 es obtener la media (al final de la columna 2, Xi) = 5,47
Paso 2, Después la columna con las diferencias (de cada nota menos la media 5,47) columna 3 (Xi-Media(5,47))
Paso 3 a la derecha, colocaremos las diferencias en valor absoluto:
Finalmente, en el paso 4, aplicamos la fórmula de la desviación media:
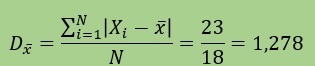
Por lo general la desviación media la utilizamos para comparar entre varias desviaciones medias, la menor de ella es la más coherente es decir más cercano los datos entre si.
Ej. en el caso que la desviación media del ejercicio anterior fuera del 3er periodo, pero, en el primer periodo fue de 1,8 en el segundo de 1,5, esto significa que en el tercer periodo (1,278) sus datos son más cercanos entre sí, no importa que sean malas o buenas notas.
Características de la desviación media:
- Todas las observaciones se usan en el cálculo
- No tiene la influencia debido a los valores altos y bajos
- Es un poco difícil trabajar con los valores absolutos
Para que te quede más claro el tema, te invito a observar el siguiente video:
ACTIVIDAD 2:
Contesta en tu cuaderno:
1. Utilizando el anterior ejemplo, Calcular la desviación media de los siguientes datos: 2, 4, 6 y 8.
2. Calcular la desviación media de los siguientes datos: 3, 5, 8, 6, 2, 4, 7 y 5.
3. VARIANZA
La varianza y la desviación estándar son medidas de dispersión o variabilidad, es decir, indican la dispersión o separación de un conjunto de datos. Hay que tener en cuenta que las fórmulas de la varianza y la desviación estándar son diferentes para una muestra que para una población.
La varianza se define como la media aritmética de los cuadrados de las diferencias de los datos con su media aritmética. Indican la dispersión o separación de un conjunto de datos
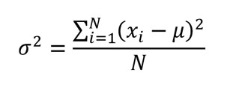
Ejemplo. De un liceo se escoge una muestra de 6 estudiantes para realizar un análisis de su masa corporal, obteniendo la siguiente información

Paso 1. Iniciaremos calculando la media o promedio, ya que es necesaria para realizar el cálculo de la varianza. Recordemos que el promedio es la suma de todos los valores dividido por el número de datos, en este caso el número de datos es n=6.
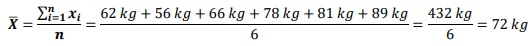
Así nuestra media es igual a 72 kg.
Paso 2. Continuaremos con el cálculo de la Varianza, para calcularla realizaremos lo siguiente: Calcularemos la diferencia entre cada uno de nuestros datos (62 kg, 56 kg, 66 kg….) con nuestra media (72 kg) y cada uno de esos resultados lo elevaremos al cuadrado
ejemplo (62 𝑘𝑔 − 72𝑘𝑔) 2 y así con todos los otros valores.
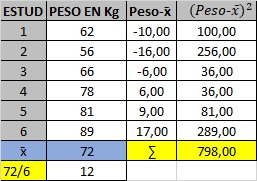
Paso 3: el resultado lo sumaremos y dividiremos por 𝑛 − 1, es decir, el número de estudiantes (6) menos 1, o sea 5, como se muestra a continuación:
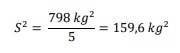
De esta manera la varianza de la muestra es 159,6 𝑘𝑔2
Te invito a observar el siguiente video sobre varianza y desviación estándar (Próximo tema)
4. DESVIACIÓN ESTÁNDAR
Se obtiene extrayendo la raíz cuadrada de la varianza. Se expresa en la misma unidad que la variable, por lo que nos puede dar una idea más cercana de los dispersos que el conjunto.
El resultado es más sencillo de lo que muestra su fórmula:
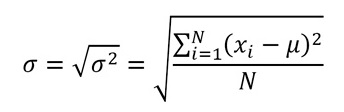
NOTA: Te recomendamos calcular primero la varianza de la población y luego sacar su raíz cuadrada para obtener la desviación estándar.
Estos son los pasos:
- Se calcula la media.
- Se calcula la varianza.
- Se calcula la desviación estándar, que es la raíz cuadrada positiva de la varianza.
Ejemplo:
Calcular la varianza y la desviación estándar de los siguientes datos: 2, 4, 6 y 8 sabiendo que corresponden a una población.
Solución:
Nos indican que estos datos forman una población, por lo tanto, usaremos las fórmulas de varianza y desviación estándar para la población, teniendo en cuenta que tenemos 4 datos, es decir, N = 4.
Paso 1: Empezamos calculando la media poblacional:
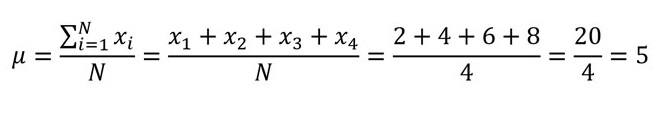
ACTIVIDAD 3:
Resuelve en tu cuaderno:
1. Calcular la desviación estándar de las notas de la alumna Juanita:
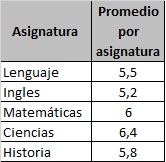
2. Un entrenador de basquetbol debe contratar a 1 jugador. Tiene 2 buenos candidatos, pero aún no sabe cuál elegir. Para tomar esta decisión decide analizar los últimos 6 juegos de ambos jugadores.
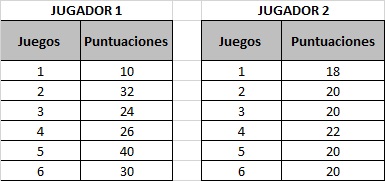
a) Calcula la media aritmética de ambos jugadores:
b) Calcular la Varianza y Desviación Estándar de ambos jugadores:
c) ¿A qué jugador elegirías para el equipo?
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad: