Grado 7 - Periodo 1

Estadística

TEMAS:

Conceptos Básicos de Probabilidad

1. Experimentos aleatorios y No aleatorios . 2. Espacio muestral. 3. Eventos y probabilidades simples.

OBJETIVO: Comprender los fundamentos de la probabilidad, incluyendo experimentos aleatorios, espacio muestral y eventos, y aplicar estos conceptos para el cálculo de probabilidades simples.

LOGRO:

• Enumerar correctamente todos los posibles resultados (espacio muestral) de un experimento aleatorio dado.

• Identificar correctamente experimentos deterministas como aquellos donde el resultado es predecible con certeza.

• Identificar correctamente experimentos aleatorios como aquellos donde el resultado no se puede predecir con certeza, incluso si se repiten bajo las mismas condiciones.

Estándar básico: Interpreto, produzco y comparo representaciones gráficas adecuadas para presentar diversos tipos de datos. (diagramas de barras, diagramas circulares.) 

Experimento aleatorio, espacio muestral, evento y probabilidad

Veamos ahora la definición clásica de probabilidad, además de las definiciones de experimento, espacio muestral y evento.

1. Experimento aleatorio

Es la reproducción controlada de un fenómeno; y cuyo resultado depende del azar. Ejemplos:

• Lanzamiento de un dado.
• Lanzamiento de una moneda.

Un experimento aleatorio puede ser repetido bajo las mismas condiciones, y se puede describir el número de resultados posibles.

2. Espacio muestral (S)

Es el conjunto de todos los resultados posibles de un experimento aleatorio.

• Si se lanza un dado, el espacio muestral está compuesto por los siguientes elementos: S={1, 2, 3, 4, 5, 6}.
• Si se lanza una moneda que tiene dos caras: perro (P) y gato (G), el espacio muestral está compuesto por: S={P, G}.
• Si se lanzan dos monedas, el espacio muestral está compuesto por: S={(P, P), (P, G), (G, P), (G, G)}.
• Si se lanza un dado y una moneda, el espacio muestral está compuesto por: S={(1,P),(1,G),(2,P),(2,G),(3,P),(3,G),(4,P),(4,G),(5,P),(5,G),(6,P),(6,G)}

Actividad1:

1. En una bolsa hay 10 bolas numeradas del 11 al 20, algunas rojas otras verdes y otras azules.

Sacamos sin mirar una bola,

• ¿cuál es el espacio muestreal numérico?
• ¿cuál es el espacio muestreal de colores?

3. Evento o suceso

Conjunto de uno o más resultados del experimento aleatorio.

• Si A = {obtener un número 5 al lanzar un dado}, entonces, A={5}.
• Si B = {obtener un número mayor que 3 al lanzar un dado}, entonces, B={4, 5, 6}.
• Si C = {obtener un número par al lanzar un dado}, entonces, C={2, 4, 6}.
• Si D = {obtener al menos 1 gato al lanzar 2 monedas}, entonces, D={(P, G), (G, P), (G, G)}

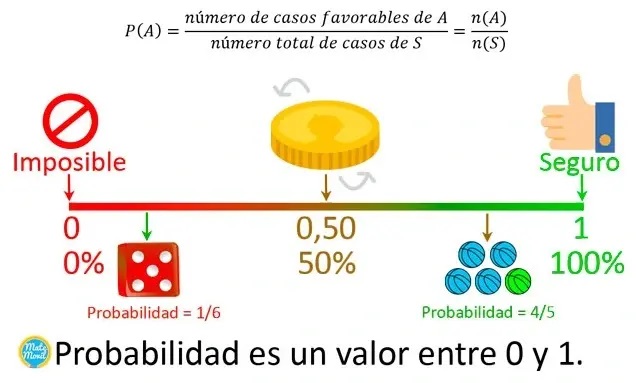
4. Probabilidad

Probabilidad es un valor entre 0 y 1, que indica la posibilidad relativa de que ocurra un evento. El valor de la probabilidad se calcula mediante la siguiente fórmula:

Recuerda que...

• El valor de la probabilidad siempre se encuentra entre 0 y 1 (incluidos ambos números), es decir, 0 ≤ P(A) ≤1.
• La probabilidad de que ocurra un evento imposible es 0. Por ejemplo, la probabilidad de obtener un 8 al lanzar un dado numerado del 1 al 6 es 0, es decir, P(X)=0.
• La probabilidad de que ocurra un evento seguro es 1. Por ejemplo, la probabilidad de obtener un número menor que 7 al lanzar un dado numerado del 1 al 6 es 1, es decir, P(X)=1.

Ejemplo 1:

Calcular la probabilidad de obtener un 2 al lanzar un dado.

Solución:

Vamos a utilizar la fórmula de probabilidad:

El experimento consiste en lanzar un dado. Luego, definimos los resultados o casos del espacio muestral.

S = {1, 2, 3, 4, 5, 6}

Definimos nuestro evento A, como obtener un 2 al lanzar un dado. Ahora, calculamos el número de casos favorables del evento A.

A = { 2 }

Ahora, empleamos la fórmula:

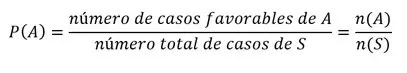
El experimento consiste en lanzar un dado. Luego, definimos los resultados o casos del espacio muestral.

S = {1, 2, 3, 4, 5, 6}

Definimos nuestro evento A, como obtener un 2 al lanzar un dado. Ahora, calculamos el número de casos favorables del evento A.

A = { 2 }

Ahora, empleamos la fórmula:

Actividad 2

En la siguiente guía de mate movil encontrarás muchísimos problemas de probabilidades resueltos, el cual debes responder el planteamiento (División) de los ejercicios del 1 al 5

En el siguiente video, vamos a revisar la definición de experimento aleatorio, espacio muestral, evento y probabilidad: