Grado 6 - Periodo 1
Matemáticas
Temas:
- Sistema de numeración decimal
- Operaciones Básicas (Adición, sustracción, multiplicación, y División).
- Potenciación y Radicación de números naturales
- Orden en naturales

DBA: Interpreta los números enteros y racionales (en sus representaciones de fracción y de decimal) con sus operaciones, en diferentes contextos, al resolver problemas de variación, repartos, particiones, estimaciones, etc. Reconoce y establece diferentes relaciones (de orden y equivalencia y las utiliza para argumentar procedimientos).

Saberes previos: (Observar video)
Quién inventó los números:
LOS NÚMEROS NATURALES
1. SISTEMA NUMÉRICO DECIMAL
En el sistema de numeración decimal cualquier cantidad se puede escribir utilizando solo 10 símbolos:
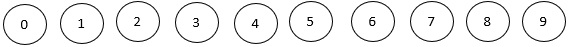
Diez unidades de un orden dado forman una unidad del orden inmediatamente superior:
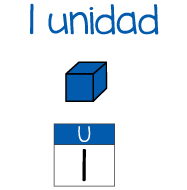
1 Unidad
Y si añadimos una a una, unidades, formaremos los números dos, tres, cuatro, cinco, etc. , hasta llegar a las 10 unidades.
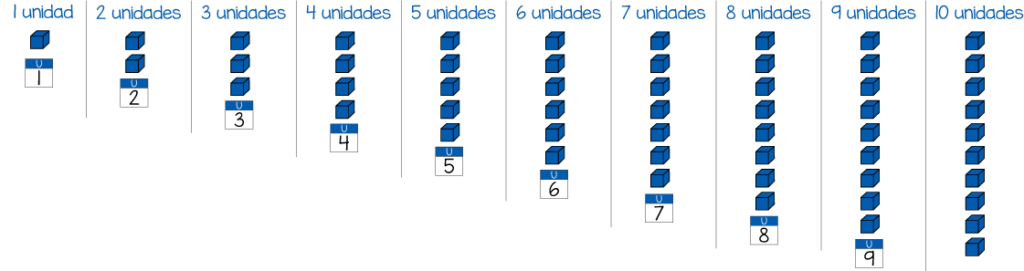
Diez unidades de un orden dado forman una unidad del orden inmediatamente superior:
10 unidades = 1 decena
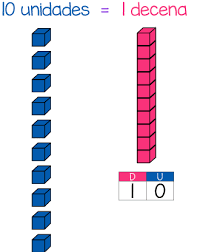
Vamos a aumentar algunas decenas más sin perder de vista el tablero de valor posicional:
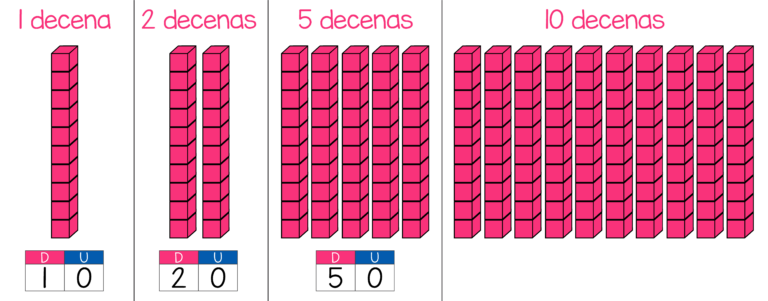
100 Unidades = 10 decena = 1 centena
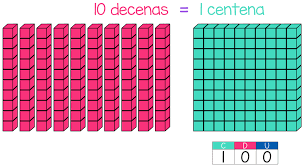
A continuación, añadiremos algunas centenas más:
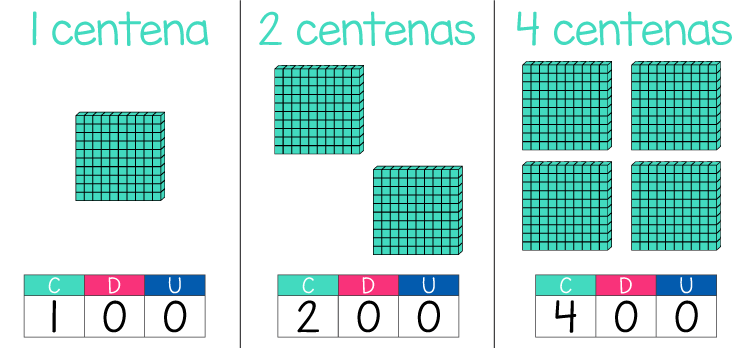
1000 Unidades = 100 decena = 1 unidad de mil
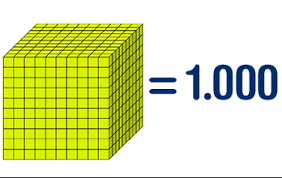
10000 Unidades = 1000 decena = 1 decena de mil
Como cada vez se hace la numeración más grande. Vamos a dar un ejemplo de ubicación de un número natural.
Ejemplo1: 145.673.294
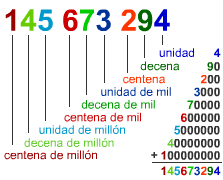
Ejemplo2:
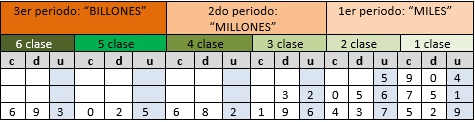
A continuación, se observa una tabla de valor posicional del número 814.372.468 , esta permite determinar el valor de las cifras de un número separados de 3 en 3 columnas:
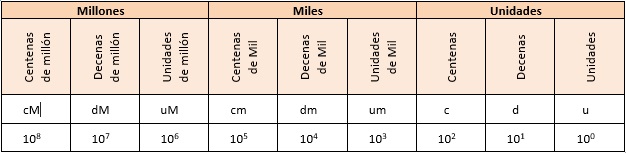

Ejemplo 3:
El número 74.305 = 7 dm + 4 um + 3 c + 0 d + 5 u
Como la suma de los valores de sus cifras
74.305 = 70.000 + 4.000 + 300 + 0 + 5
Con su desarrollo exponencial:
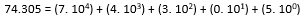
Ejemplo4:
Para números grandes se puede organizar ordenes, clases y periodos. Cada orden comprende unidades, decenas y centenas (sean de millar, millón.). Cada tres órdenes forman una clase. Dos clases forman un periodo. Fíjate que, aunque el número se empieza a escribir por tu izquierda, los órdenes se empiezan a colocar por tu derecha (unidades, decenas…)
Vamos a colocar los siguientes números:
- 5.904
- 32'056.751
- 693.025''682.196'437.529
Practica jugando en el siguiente link, muestra los resultados al docente:
https://www.cerebriti.com/juegos-de-matematicas/sistema-de-numeracion-decimal
AHORA OBSERVEMOS QUE TANTO HAS APRENDIDO
Actividad 1:
1. Observa las imágenes y completa las tablas de valor posicional, responde en tu cuaderno de matemáticas. Yo resolveré el primer ejercicio:
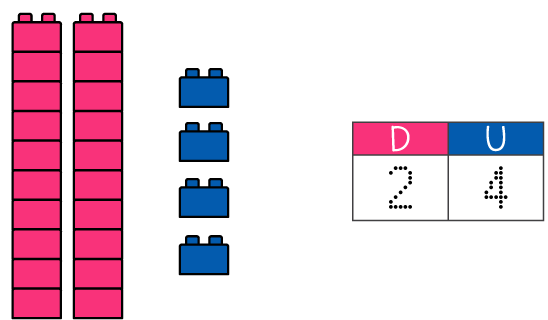
2:
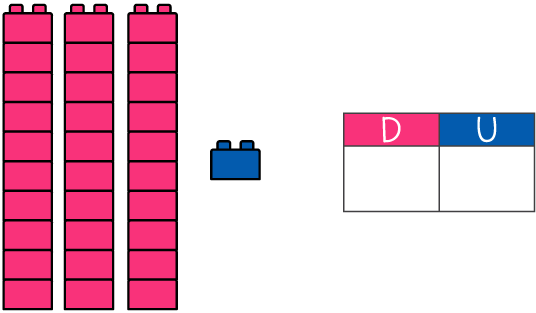
3:

4:
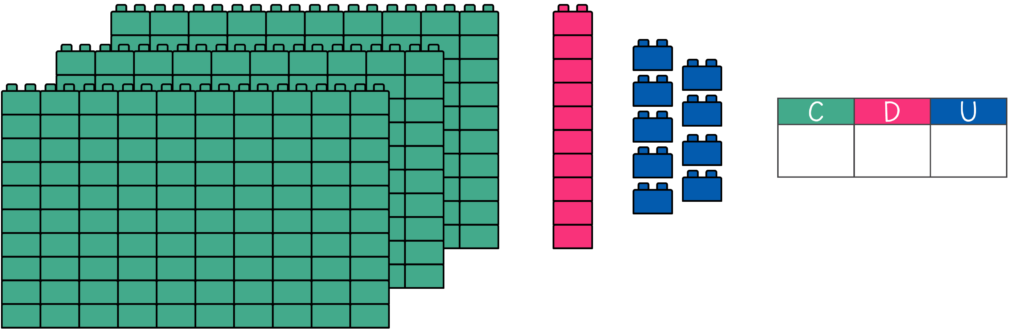
5:
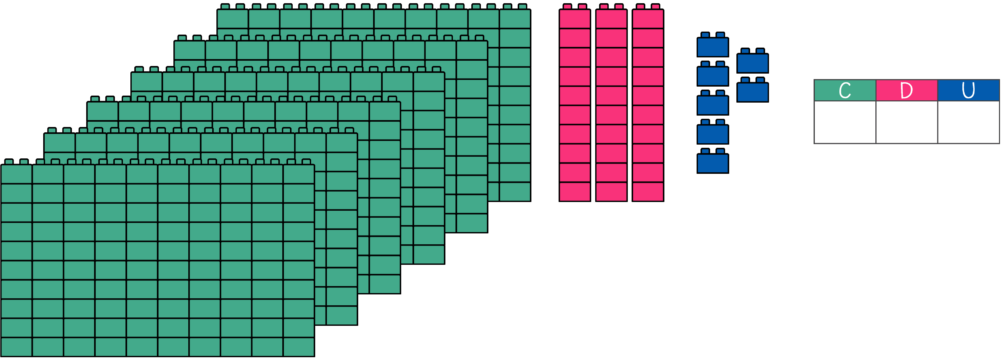
6:
En el siguiente ejercicio hay que completar los recuadros en blanco a partir de la cantidad de cubitos en la imagen
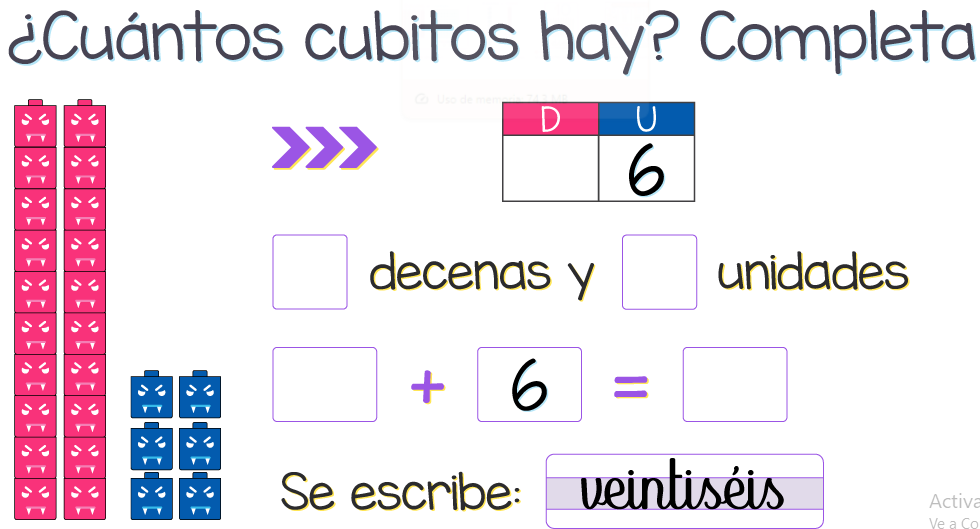
7:
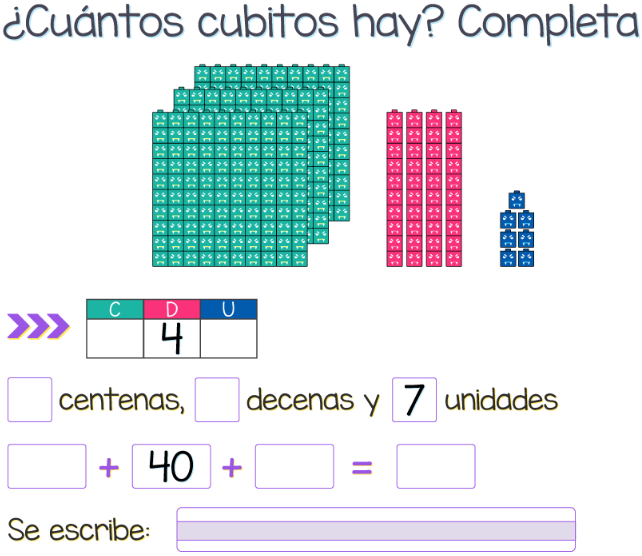
8.
Resuelve los siguientes ejercicios en el siguiente enlace: https://www.liveworksheets.com/w/es/matematicas/178620
Refuerzo: En el siguiente video, vamos a ver muchos ejemplos más de unidades, decenas y centenas.
EL CONJUNTO DE LOS NÙMEROS NATURALES
Es posible imaginar un gran conjunto universal formado por muchísimos conjuntos. Si los conjuntos son seleccionados según el número de elementos que poseen, se obtienen clases de conjuntos muy particulares. Por ejemplo , la clase de los conjuntos con un elemento, la clase de los conjuntos con dos elementos, la clase de los conjuntos con tres elementos, etc.
Si a cada clase se le asigna un nombre y un símbolo que la representa, surge el conjunto de los números naturales. Así, a la clase de los conjuntos con un único elemento se le asigna el símbolo 1; a la clase de los conjuntos con dos elementos se le asigna el símbolo 2; a la clase de los conjuntos con tres elementos se le asigna el símbolo 3 y así ssucesivamente.
Un número natural es el símbolo que representa a una clase de conjuntos con el mismo número de elementos o con el mismo número cardinal.
El símbolo que representa el conjunto de los números naturales es N , por lo
tanto,
N = {1, 2, 3, 4,..}
Los números naturales son aquellos que permiten contar los elementos de un conjunto.
Se trata del primer conjunto de números que fue utilizado por los seres humanos para contar objetos.
Existe una controversia respecto a considerar al cero
(0) como un número natural. Por lo general, la Teoría de Conjuntos incluye al cero dentro de este grupo, mientras que la Teoría de Números prefiere excluirlo.
N = {0,1, 2, 3, 4,..} es el conjunto de los números naturales y el cero.
Representación de los números naturales en la Recta numérica.
Para representar los números naturales en la recta numérica lo hacemos siguiendo los siguientes pasos:
1. Dibujamos la recta, dividida en partes iguales y colocamos el 0 en la izquierda
2. El conjunto de los números naturales es ilimitado, ya que a cada número le sigue siempre otro número. Los números naturales se pueden representar en una semirrecta numérica del siguiente modo:

Orden y representación de los números naturales.
Los números naturales están ordenados: el 0 es menor que el 1, el 1 es menor que el 2, etc... En vez de escribirlo así, para ahorrar tiempo y espacio en matemáticas se escribe con el símbolo <. Por ejemplo, para decir:
El 3 es menor que el 7" se escribe: 3 < 7
De la misma forma, para decir "es mayor que" usaremos el símbolo "
"5 es mayor que 1" se escribe: 5 >1 .

Suma o adición de números naturales
ADICIÓN

La suma es la operación matemática que resulta al reunir en una sola varias cantidades. También se conoce la suma como adición. Las cantidades que se suman se llaman sumandos y el resultado suma o total. Para su notación se emplea entre los sumandos el signo + el cual se lee "más".
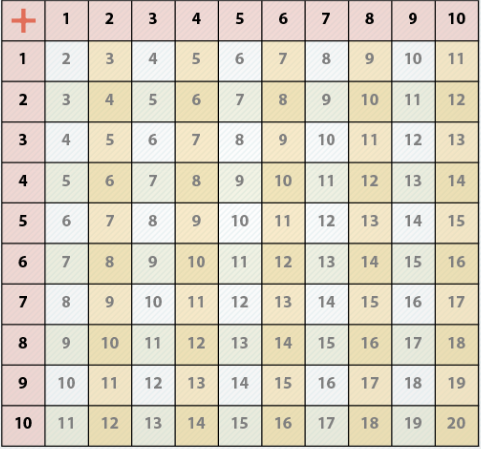
Suma de dos números de una sola cifra La suma de dos números de una sola cifra se halla mentalmente, una vez que se ha aprendido la tabla de la suma. Observa detalladamente la siguiente tabla:a + b = c
PROPIEDADES DE LA SUMA
Las propiedades nos indican en que orden son válidas las operaciones con los números naturales. Ellas son:
1. Clausurativa:
2. Asociativa
3. Conmutativa
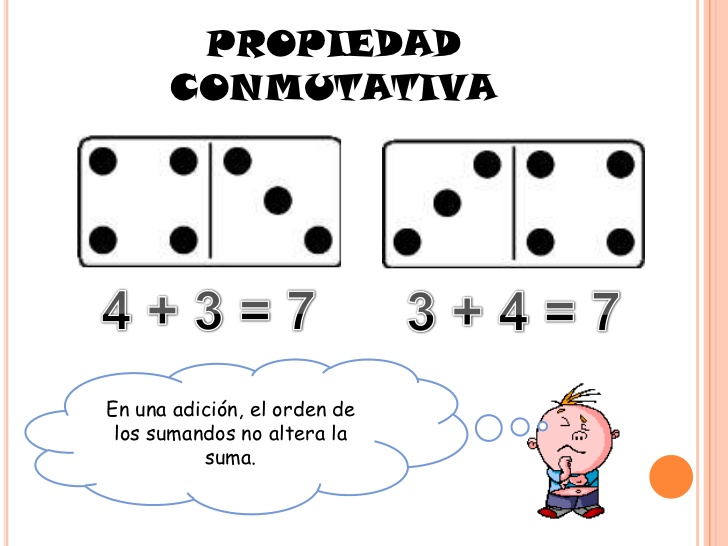
Actividad 2:
Razonamiento Lógico, Solución de Problemas y Operaciones Básicas
Responder en el cuaderno:
- En los siguientes ejercicios se encuentran unas sumas realizan los ejercicios e identifican que propiedad es:
- (8 + 7) + 5 = 8 + (7 + 5) _____ __________
- (2 + 16) = (16 + 2) _____ __________
- 215 + 0= _____ __________
2. En el siguiente ejercicio aplica las propiedades conmutativa y asociativa juntas y resolverlo.
12 + 15 + 7 + 2=
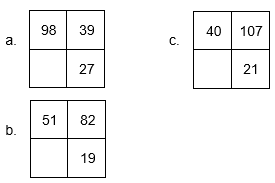
3. Escribir el número que falta en cada cuadrado, teniendo en cuenta que la suma de todos los números debe ser 200
Sugerencia para este punto:
Primero : sume los tres valores que hay, Segundo : Reste 200 menos la suma de los tres números del cuadro, Así:

1º) 107 + 42 + 23 = 172
2º) 200 – 172 = 28
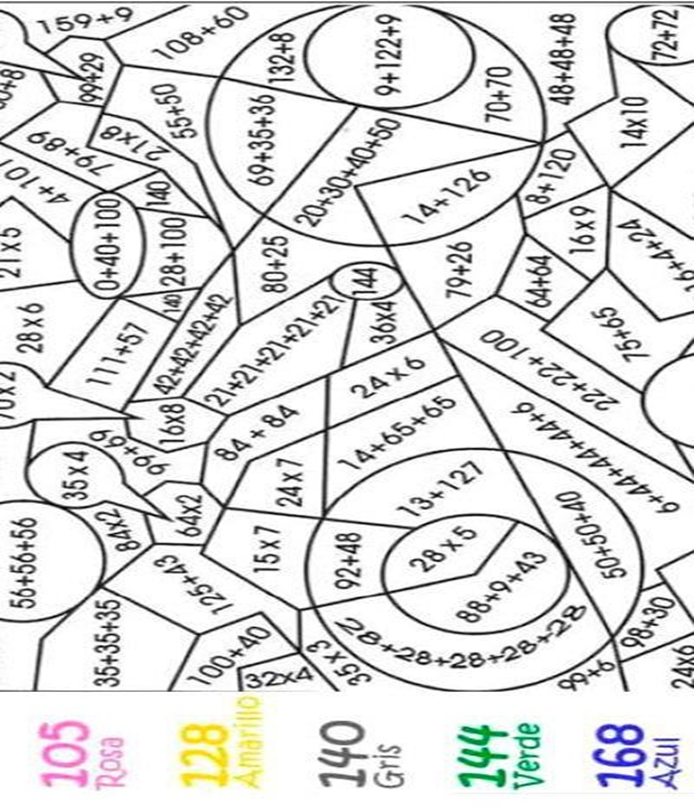
Actividad 3:
Mate Arte: Artística y Matemática . En esta actividad lúdica los estudiantes de 6º van a realizar las operaciones que se encuentran en cada zona del dibujo comparando su resultado con una escala de 5 valores que tienen asignados colores distintos y que se encuentran en la parte inferior del cuadro, el estudiante coloreara la zona con un lápiz del color que corresponde al valor de la suma obtenida en dicha zona. Por ejemplo, si la suma en la zona es 9 +122+9 = 140, esta zona se debe colorear de gris según la escala.
NOTA : Para esta actividad te sugerimos que pegues la imagen en Paint y utiliza la opción de relleno de acuerdo a los colores o en su defecto pégala en word e imprímela para después colorearla y pegarla en tu cuaderno.

Resta o sustracción de números naturales
SUSTRACCIÓN

La sustracción o resta de números naturales es
una operación que consiste en quitar o separar de un número mayor
otro número menor, para hallar la diferencia entre dos números. Los términos de la sustracción son: Minuendo,
Sustraendo
y diferencia
M = Minuendo: es el número al que se le resta.
S = Sustraendo: es el número que se le resta o quita al minuendo.
D = Diferencia:resultado de la operación.
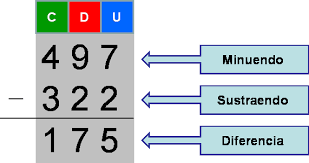
Procedimiento para realizar la sustracción o resta de
dos números naturales
Se toma el minuendo (cantidad mayor) y el sustraendo (cantidad menor), y se organizan las unidades debajo de las unidades, las decenas debajo de las decenas, así sucesivamente y se resta.
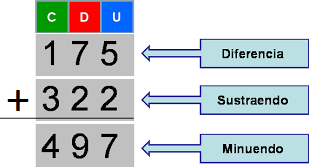
Prueba de la Resta.
Para probar si el resultado de una resta es correcto, se toma la diferencia y se le suma el sustraendo y tiene que dar como resultado el minuendo.
Diferencia + sustraendo = Minuendo. D + S = M
PROPIEDADES DE LA RESTA
La resta NO tiene propiedades, pero sigue varios patrones importantes; es anticonmutativa, lo que significa que el cambio del orden cambia el signo de la respuesta. No es asociativa, lo que significa que cuando se restan más de dos números, importa el orden en el que se realiza la sustracción. Restar 0 no cambia un número.
Actividad 4:
Ejercicios de resta:
1. En la siguiente tabla se muestran cinco planetas del sistema solar, su diámetro y su distancia al sol.
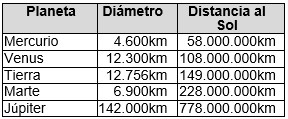
- ¿Cuál es el Planeta con mayor diámetro? ¿Qué diferencia en kilómetros tiene el diámetro de este planeta con el diámetro de la tierra?
- Qué número es mayor, el diámetro de la Tierra, Venus, Marte y Mercurio juntos o el diámetro de Júpiter.
- Calcular la diferencia entre el diámetro de la tierra y el diámetro de mercurio.
2. Observa el número aproximado de habitantes de cuatro departamentos colombianos:
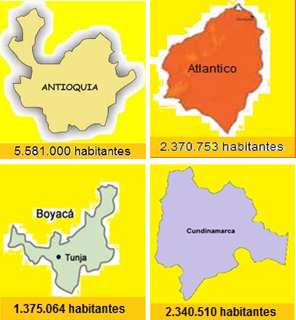
· Averiguar donde viven Alba, José, Ana y Jairo si se sabe que:
a. Alba vive en el departamento que tiene 3.190.247 habitantes menos que Antioquia.
b. José vive en el departamento que tiene 965.446 habitantes más que Boyacá.
c. Ana vive en el departamento que tiene más habitantes.
d. Jairo vive en el departamento que tiene 995.689 habitantes menos que atlántico.
3. Problema. Usando cubitos de madera, Pedro construyo la figura que se muestra. ¿Cuántos cubitos uso?
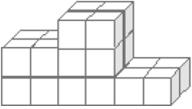
(a) 12 (b) 18 (c) 19 (d) 22 (e) 24
4. Realiza las siguientes
Sustracciones y cuando termines verifica
si la respuesta es correcta
realizando la prueba:


Multiplicación de números naturales
Multiplicación

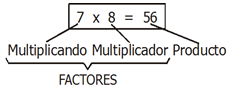
Toda multiplicación de dos números naturales nos da como resultado otro número natural. Al igual que en el caso de la suma, el resultado o producto de una multiplicación será otro número natural siempre que los factores pertenezcan a ese conjunto. Los términos de la sustracción son: Factor y producto
F1 = Factor1: es el número al que se le multiplica, también se le conoce como multiplicando.
F2 = Factor2: es el número que multiplica también se le conoce como multiplicador
P = Producto: resultado de la operación.
La multiplicación o producto de dos números naturales es una forma abreviada de expresar la suma repetida de un número. Si a y b son números naturales, su multiplicación se define como la suma repetida del número a una cantidad de veces igual al número b y se utiliza el símbolo "+":
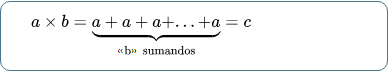
PROPIEDADES DE LA MULTIPLICACIÓN
Procedimiento para Multiplicar por dos, tres o mas cifras

Actividad 5:
1. Problema. Miguel escogió un número, lo multiplicó por sí mismo, luego sumó 1, multiplicó el resultado por 10, a lo que obtuvo le agregó 3 y luego multiplicó su resultado por 4. El resultado de todo esto fue 2012.
¿Qué número escogió al principio?
(a) 7 (b) 8 (c) 9 (d) 11 (e) 13
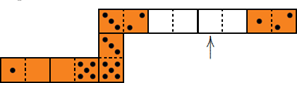
2. Problema. Pancho hizo una hilera con 7 fichas de dominó de manera que los lados con el mismo número de puntos quedaran uno al lado del otro. Originalmente la hilera tenía un total de 33 puntos, pero el hermanito de Pancho se llevó dos de las fichas.
¿ Qué cantidad de puntos había en el lugar que señala la flecha en la figura?
3. Realiza las siguientes Multiplicaciones
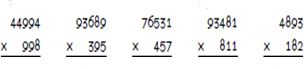

División de números naturales
DIVISIÓN

La división es la operación inversa a la multiplicación. Nos dice cuántas veces una cantidad llamada dividendo contiene a otra cantidad llamada divisor. La cantidad resultante de la operación se llama cociente.
También la podemos entender como la operación mediante la cual distribuimos una cantidad (el divisor) en determinado número (el dividendo) de partes iguales
Se denota con el símbolo , mediante una barra inclinada (/) o en forma de fracción (a/b) y tiene la siguiente forma:
Se denota con el símbolo ÷, mediante una barra inclinada ( / ) o en forma de fracción ( 𝑎 ) y tiene la siguiente forma
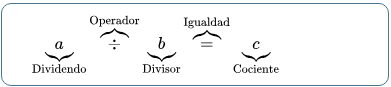
Por ser la operación inversa a la multiplicación, podemos definirla en términos de esta última como el número (cociente) por el que debemos multiplicar el divisor para obtener el dividendo. Por ejemplo:

Divisiones exactas
En la división exacta, la igualdad a÷b=c se cumple porque tenemos suficientes unidades en el dividendo (a) para distribuirlas en una cantidad de grupos igual al divisor (d), todos de tamaño igual al cociente (c). Los siguientes son ejemplos de divisiones exactas:

Divisiones inexactas
En la división inexacta no se cumple la igualdad porque no existe un número natural que nos permita repartir las unidades del dividendo en una cantidad de grupos iguales. Cuando lo intentamos nos quedan unidades sobrantes. A esas unidades sobrantes las llamamos residuos de la operación.
En el siguiente ejemplo, al dividir 23 entre 5 obtenemos un cociente de 4 unidades (grupos completos) y un residuo de 3 unidades (las unidades restantes):
23=(5x4)+3
Otros ejemplos de divisiones inexactas son:
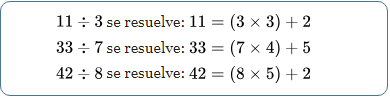
Nota: La división donde el divisor es 0 NO tiene solución en el conjunto de los números naturales.
Dividir un número por cero (a÷0=?) es equivalente a encontrar un número que multiplicado por 0 números del dividendo (0×?=a). Pero debido a que el 0 es el elemento absorbente en la multiplicación, el resultado de multiplicar por cero siempre es cero. Por eso no existe ningún número que multiplicado por cero nos de un resultado diferente de cero.
La división 0÷0 tampoco está definida porque al escribir 0÷0=? como multiplicación obtenemos 0×?=0. ¿Al reemplazar? con los primeros números naturales obtenemos:

PROPIEDADES DE LA DIVISIÓN
La división no es conmutativa
Conmutar significa cambiar una cosa por otra. La propiedad conmutativa hace referencia al intercambio del orden de la operación . Es decir, si resulta lo mismo a÷b que b÷ a. Veamos a través de un ejemplo que la división no cumple esta propiedad.
Si realizamos 2÷ 1 obtenemos como resultado 2. Por otra parte, si tratamos de resolver 1÷ 2 obtendremos que el resultado ni siquiera es un número entero, pues estamos dividiendo una sola unidad entera en dos partes iguales.
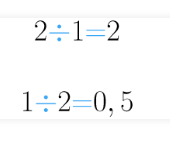
La división no es asociativa
La propiedad asociativa dice que cuando se tiene una expresión como 24÷ 4÷ 2 es posible realizarla de dos formas: asociando los dos primeros números, o los dos últimos . Lo anterior quiere decir que, de cumplirse la propiedad asociativa, se debe tener (24÷ 4)÷ 2=24÷ (4÷ 2), Veamos si esto se cumple:
Resolvamos primero Operando en el orden que indican los paréntesis se realiza primero Luego se opera obteniendo el resultado final.
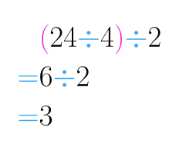
Por otra parte, resolviendo 24÷ (4÷ 2), se empieza por 4÷ 2
que da como resultado 2. Después se realiza 24÷2
así llegamos a la respuesta final.
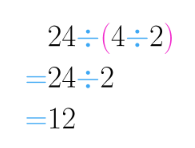
Como te puedes dar cuenta los resultados finales fueron distintos, de esta forma podemos concluir que la división no cumple la propiedad asociativa.
Nota: Cero (0), divido por cualquier número siempre dará Cero (0)
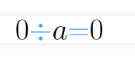
PASOS PARA LA DIVISIÓN POR DOS CIFRAS
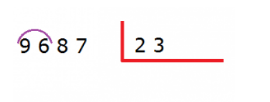
1. Toma las primeras cifras del dividendo, el mismo número de cifras que tenga el divisor. Si el número que has tomado del dividendo es más pequeño que el divisor tienes que tomar la siguiente cifra del dividendo.
En este ejemplo queremos dividir 9687 entre 23. El divisor (23) tiene 2 cifras por lo tanto tendremos que tomar las 2 primeras cifras del dividendo (96).
Como 96 es mayor que 23 podemos dividirlo.
2. Divide el primer número del dividendo (o los dos primeros números si en el paso anterior has tenido que tomar otra cifra más) entre la primera cifra del divisor. Escribe el resultado de esa división en la parte del cociente.
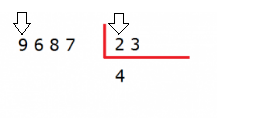
La primera cifra del dividendo es 9 y la primera del divisor es 2, por lo tanto tenemos que dividir 9 entre 2
9 : 2 = 4. Escribimos el 4 en el cociente.
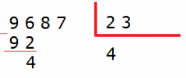
3. Multiplica la cifra del cociente por el divisor, el resultado escríbelo debajo del dividendo y réstalo. Si no se puede porque el dividendo es más pequeño tendrás que escoger un número más pequeño en el cociente hasta que se pueda restar.
Multiplicamos el cociente (4) por el divisor (23): 4 x 23 = 92
Escribimos el resultado de la multiplicación debajo del dividendo (96) y restamos los dos números:
96 – 92 = 4
4. Una vez hecha la resta baja la cifra siguiente del dividendo y vuelve a repetir los pasos desde el punto 2, hasta que no queden más números en el dividendo.
Ahora bajamos la siguiente cifra del dividendo (8).
Ahora tenemos que dividir 48 entre 23 repitiendo los mismos pasos que antes.
¿Sabría continuar tú solo?
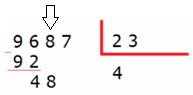
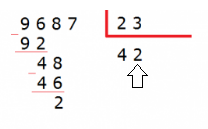
Dividimos 48 entre el divisor: 48 : 23 = 2
Escribimos el 2 en el cociente y lo multiplicamos por el divisor:
2 x 23 = 46.
Escribimos el 46 debajo del dividendo y restamos:
48 – 46 = 2

Bajamos la siguiente cifra: el 7.
Ahora tenemos que dividir 27 entre 23: 27 : 23 = 1
Escribimos el 1 en el cociente y lo multiplicamos por el divisor: 1 x 23 = 23
Ahora restamos 27 – 23 = 4
Como ya no quedan más cifras en el divisor ya hemos terminado de hacer la división de 2 cifras.
El resultado es 421 y el resto o residuo es 4.
¿Has aprendido a hacer ejercicios de división de 2 cifras?
Bien, ahora ya que has aprendido, observa el siguiente video para reforzar tus conocimientos:
Actividad 6:
Resuelve los siguientes problemas
1) Juan tenía 220 canicas y las quería regalar a sus amigos. ¿Cuántas canicas les dará a sus amigos si las tiene que repartir entre 10?
2) La mama de Eunice les compro dos pizzas de 16 porciones cada una y las tiene que dividir entre su familia que son 4 miembros. ¿Cuantas porciones les tocara a cada uno si el padre se comerá 7?
3) Tenemos 45 bombones y queremos repartirlos entre 9 niños por lo que tenemos que formar 9 grupos con el mismo número de bombones.
4) Une cada división con su repuesta
a)125/5 a)6
b)12/4 b)25
c)36/6 c)20
d)200/10 d)3
5. Realiza las siguientes divisiones y cuando termines verifica si la respuesta es correcta realizando la prueba:

Operaciones varias:
6. Mategrama o Crucigrama Matemático: aplicado a las operaciones básicas. Los estudiantes de 6º realizaran las operaciones básicas que se encuentran a la derecha del crucigrama y luego escribirán sus resultados en letras sin equivocaciones, y luego llenaran el crucigrama con las palabras que corresponde en la horizontal o vertical según sea el caso. Por Ejemplo, Horizontal
10. 5x3= 15 , en la horizontal 10 va la palabra quince.

NOTA:
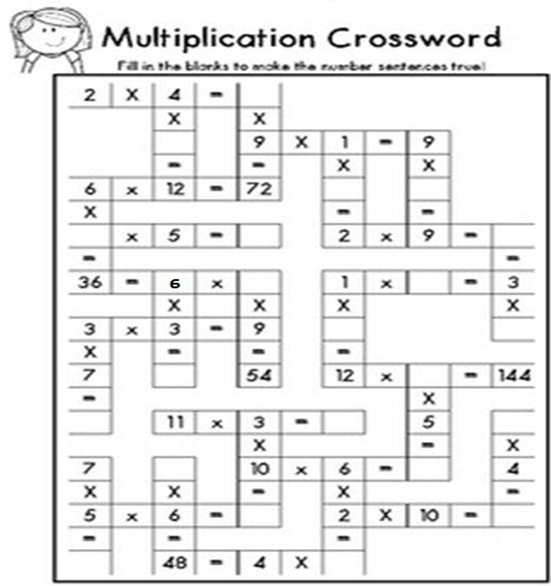
7. Crucigrama Matemático con la multiplicación: El estudiante de 6º llenará los espacios en blanco con los resultados de la multiplicación de dos números que estén operando con el signo X.
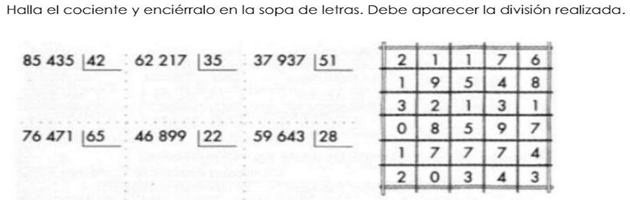
8. Sopa de letras Matemático con la división por 2 cifras: El estudiante de 6º primero realizara la división en su cuaderno de apuntes de manera muy organizada y luego buscara el cociente obtenido en la sopa de letras para encerrarlo con un ovalo.
POTENCIACIÓN Y RADICACIÓN DE NÚMEROS NATURALES
RECORDEMOS
Una multiplicación formada por factores iguales se puede escribir en forma de potencia:
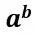
donde a, conocida como la base, es el número que se repite y b, conocido como el exponente, es el número de veces que se repite el factor.
Por ejemplo, tendríamos que
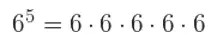
Para este ejemplo de potencia tendríamos que la base es 6, mientras que el exponente es 5.
1. POTENCIA DE NÚMEROS NATURALES
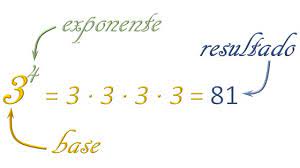
1.1. POTENCIAS CON EXPONENTES ENTEROS
A. Potencia con exponente entero positivo

B. Potencia con exponente entero negativo
Una potencia con exponente negativo es igual al inverso multiplicativo de la base de la potencia elevado al exponente positivo (siempre que la base sea distinta de cero).
Así, tenemos que:
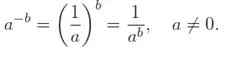
A. Potencia de número positivo
Cuando en una potencia la base es fraccionaria, elevamos tanto el numerador como el denominador al exponente.
B. Potencia con base fraccionaria y exponente negativo
Una potencia con base fraccionaria y exponente negativo es igual al inverso multiplicativo del base elevado al exponente positivo. Recordemos que el inverso de una fracción es igual a cambiar el numerador y el denominador entre sí, esto es, el inverso
PROPIEDADES DE POTENCIACIÓN
Las propiedades de las potencias nos permiten manipularlas y simplificar expresiones complejas de manera eficiente. Estas propiedades son fundamentales para trabajar con operaciones matemáticas avanzadas.
1. Producto de potencias de la misma base

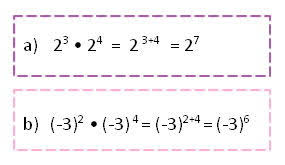
2. Cociente de potencias de la misma base
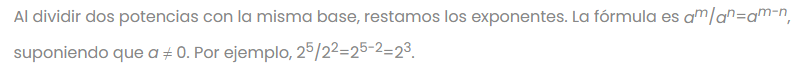
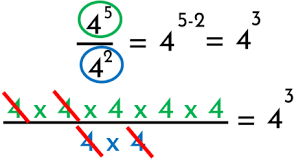
3. Potencias con exponente nulo


4. Potencias de exponente negativo

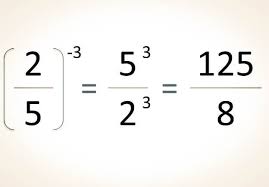
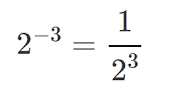
5. Potencia de una potencia

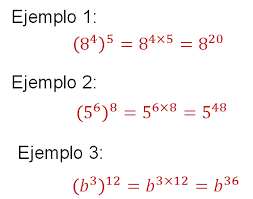
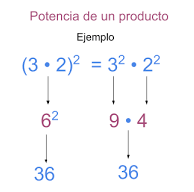
6. Potencia de un producto

7. Potencia de un cociente


Tabla de Propiedades de las Potencias
Para consolidar nuestro entendimiento de las propiedades de las potencias, te dejo esta tabla. sirve como una referencia rápida para recordar cómo manipular potencias bajo diferentes operaciones. A continuación, se presenta una tabla resumen con las propiedades más importantes de las potencias discutidas previamente:

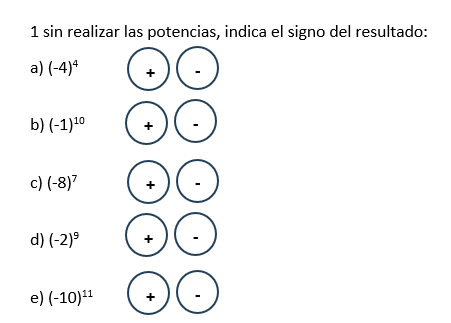
Nota: Una base negativa con exponente impar su resultado será negativo y si su esponente es par su resultado es positivo.
Si no te quedó claro el concepto, te invito a que observes este video:
Video:
Actividad 7:
1. Desarrolla los 10 ejercicios que se encuentra en el siguiente link interactivo, anota los resultados en tu cuaderno y entrégalo al docente.
Actividad 8:
TODAS LAS RESPUESTAS DE LOS EJERCICIOS DEBEN JUSTIFICARSE CON LAS RESPECTIVAS OPERACIONES, PROCEDIMIENTOS O PROCESOS.





2· RADICACIÓN
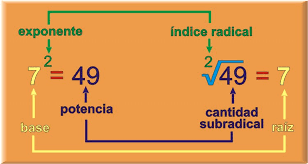
La radicación es una de las operaciones inversas de la potenciación, que nos permite conocer la base de la potencia cuando se conocen la potencia y el exponente. Los elementos o partes de la radicación son:
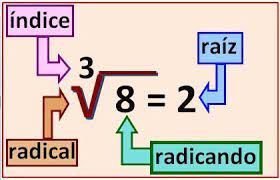
Las partes que forman una Radicación:
1. Radical: Es el símbolo de la operación √
2. Índice: el número que indica cuántas veces deberá multiplicarse por sí misma la raíz, esto se realiza con el propósito de conseguir el radicando.
3. Radicando o Cantidad subradical: Es el número que le vamos a calcular la raíz, el número que se encuentra dentro del radical, es decir, que le señalaría al índice cuál es el resultado que debe dar el número que se desempeñe como raíz, cuando se multiplique por sí mismo, tantas veces como señale el índice.
4. Raíz: Es el número que multiplicado la cantidad de veces que indica el índice da como resultado el
radicando.
Nombre de la raíz según su índice: De acuerdo con su índice, la raíz recibe nombres particulares:
- Para el índice 2 (si el índice es 2, se suele omitir) se le llama raíz cuadrada.
- Para índice 3, se llama raíz cúbica.
- índice 4, raíz cuarta
- índice 5, raíz quinta, y así sucesivamente, es decir se nombra el número ordinal.

Propiedades de la Radicación:
Las propiedades de la radicación son similares a las de la potenciación puesto que la raíz es una potencia con
exponente fraccionario.


Actividad 9:
1. Expresa en forma de raíz las siguientes potencias:

2. Escribe en forma de potencia las siguientes raíces:
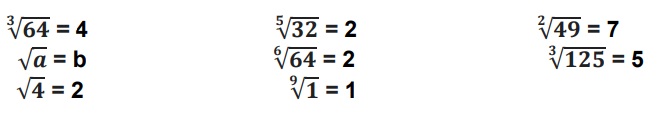
3. Halla los resultados de las siguientes raíces:
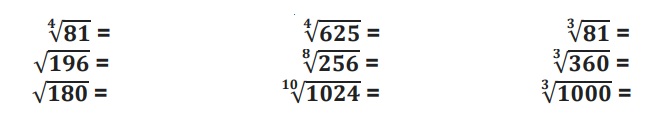
4. Simplifica cada caso utilizando las propiedades de la radicación.
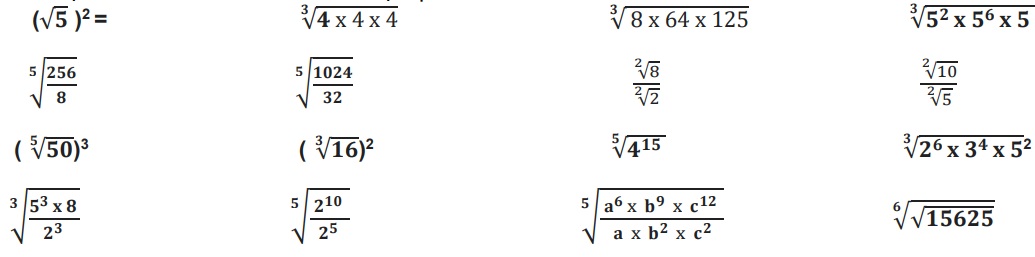
5. Completa la siguiente tabla: Observando el ejemplo

HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad: