Grado 6 - Geometría
Periodo 3

TEMAS:
Cuadriláteros
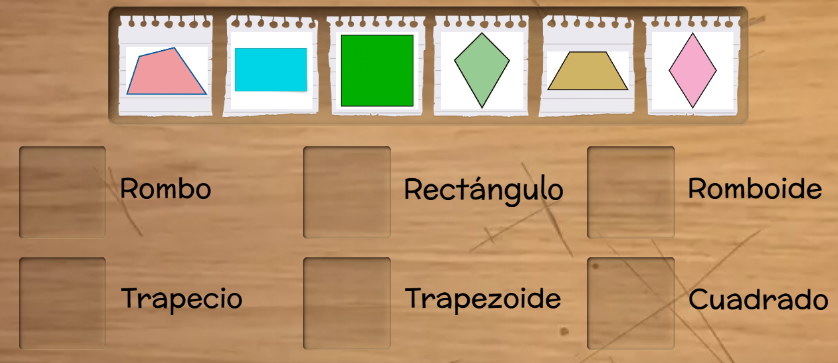
- Clasificación de cuadriláteros (cuadrados, rectángulos, rombos, trapecios)
- Propiedades y características de los cuadriláteros.
- Perímetro y área de cuadriláteros.
Círculos
- Elementos del círculo (radio, diámetro, circunferencia)
- Propiedades y características del círculo.
- Perímetro (circunferencia) y área del círculo
DBA7 . Reconoce el plano cartesiano como un sistema bidimensional que permite ubicar puntos como sistema de referencia gráfico o geográfico.
Estándar Básico de aprendizaje: Identificador de características de localización de objetos en sistemas de representación cartesiana y geográfica.
CUADRILÁTEROS
Los cuadriláteros son polígonos de cuatro lados, cuatro vértices y cuatro ángulos interiores. La suma de sus ángulos interiores es igual a 360°. Además, tienen 2 diagonales.
1. CLASIFICACIÓN (tomado de: https://www.wited.com/cuadrilateros-y-su-clasificacion/)
Los cuadriláretos tienen tres clasificaciones principales: paralelogramos, trapecios y trapezoides.
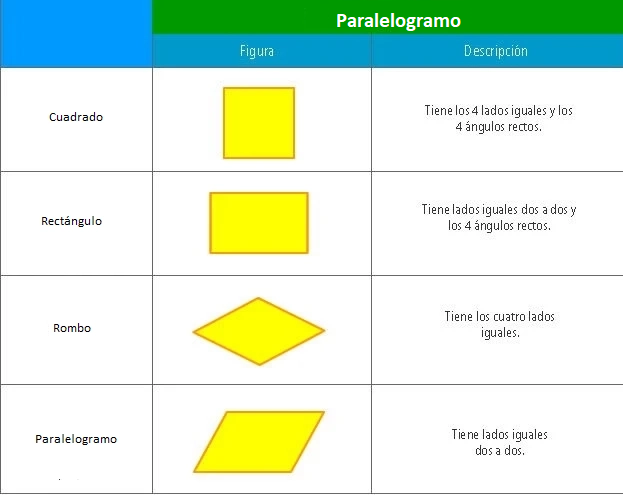
1.1. Paralelogramo
Son las figuras de 4 lados que son paralelos dos a dos, es decir, poseen dos pares de lados paralelos. Se clasifican en:
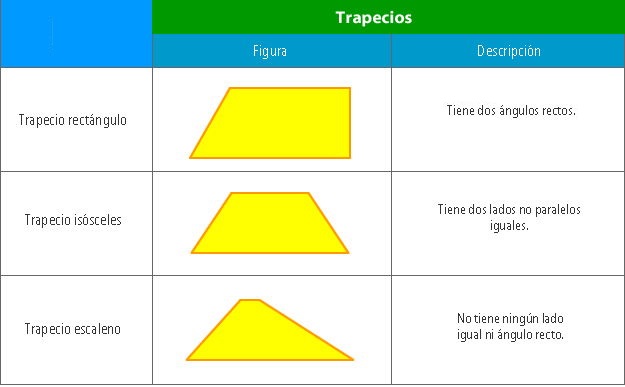
1.2. Trapecios
Cuadriláteros que tienen dos lados paralelos, llamados base mayor y base menor y otros dos lados no paralelos. Se clasifican en:
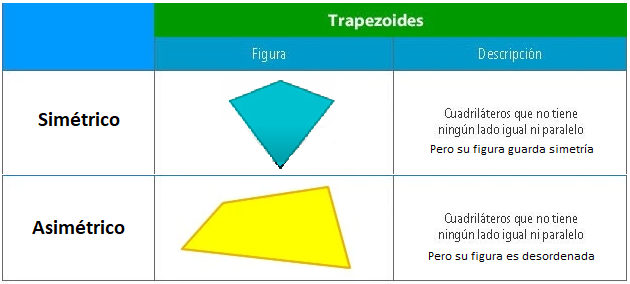
1.3. Trapezoides
Cuadriláteros que no tiene ningún lado igual ni paralelo.
Paraca reforzar el tema te invito a observar el siguiente video
Actividad 1:
Te invita a clasificar los cuadriláteros a través del siguiente juego en línea (Enséñale los resultados a tu docente):
2. · Perímetro y área de cuadriláteros
2.1. Perímetro
El perímetro de un cuadrilátero se define como la longitud total de su frontera. Es decir, es la suma de todos sus lados. Así, si tuviéramos un cuadrilátero ABCD
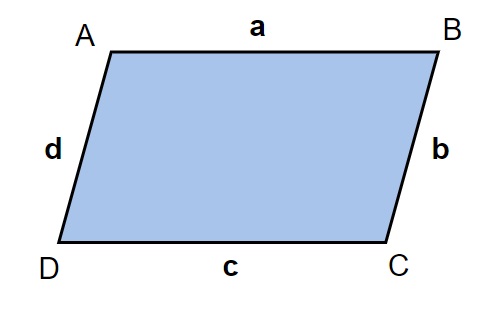
El perímetro de los cuadriláteros, con los lados AB, BC, CD y DA , el perímetro, P es
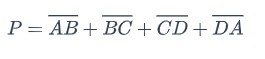
o
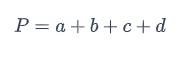
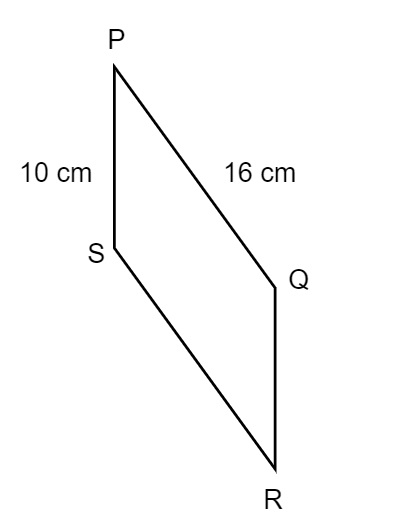
Ejemplo 1: Hallar el perímetro del siguiente cuadrilátero
Solución
Recuerda que un paralelogramo tiene lados opuestos de igual longitud. Esto significa que PQ = SR y PS = QR. Así, SR = 16 cm y QR = 10 cm. PQ = SR y PS = QR. Así, SR = 16 cm y QR = 10 cm.PS = QR. Así, SR = 16 cm y QR = 10 cm.SR = 16 cm y QR = 10 cm. Distancia entre ejes: 10 cm.
Para hallar el perímetro de esta forma dada, simplemente sumamos la longitud total de cada lado como se ha mencionado.
P=16+16+10+10⇒P=2(16)+2(10)⇒ P=32+20⇒ P=52cm P=32+20⇒ P=52cm P=52cm
Así, el perímetro de este paralelogramo es de 52 cm.
Ejemplo 2:
Halla la longitud de los lados que faltan de la cometa de abajo dado que el perímetro es igual a 98 cm.
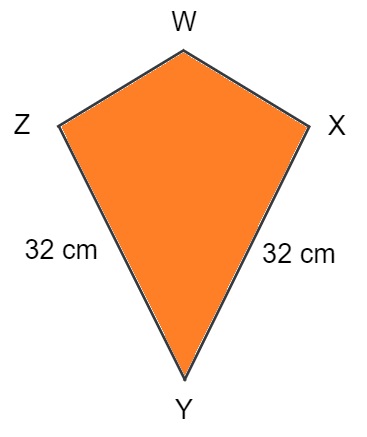
Solución:
En primer lugar, ten en cuenta que una cometa tiene dos pares de lados adyacentes iguales. Esto significa que WZ = WX (e YZ = YX = 32 cm).
Por la fórmula del perímetro de un cuadrilátero, obtenemos
P=32+32+WX+WZ⇒98=64+WX+WX⇒98=64+2WX
Reordenando esto, obtenemos:
64+2WX=98⇒2WX=98-64⇒2WX=34
Simplificando aún más, WX=34/2⇒WX=17cm.
Por tanto, la longitud de WX y WZ es de 17 cm.
2.2. perímetro de cuadriláteros en un plano
Supongamos que te dan un conjunto de cuatro puntos, (x, y), en un plano cartesiano. Uniendo estos puntos con cuatro segmentos de recta (separados), encontramos que forma la figura de algún cuadrilátero. A continuación, se te pide que halles el perímetro de esta forma utilizando estas coordenadas. ¿Hay algún método que podamos utilizar para conseguirlo?
Para abordar este problema, utilizaremos la fórmula de la distancia. Se presenta a continuación.
Fórmula de la distancia
Dados dos puntos A(x1, y1) y B(x2, y2), la distancia entre A y B, denotada por DAB, se halla utilizando la fórmula siguiente.
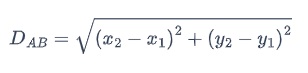
Dicho esto, podemos hallar el perímetro de este cuadrilátero calculando la distancia de estos cuatro segmentos de recta (formados por su correspondiente par de puntos) y sumándolos todos.
Nota: Dado un conjunto de cuatro puntos, puede ser útil que esboces el contorno de este cuadrilátero para que podamos calibrar aproximadamente el tipo de cuadrilátero con el que estamos tratando. De este modo, nos daremos cuenta de sus distintas propiedades y podremos calcular su perímetro de forma mucho más eficaz.
Para verlo mejor, veamos los ejemplos siguientes.
Ejemplo:
Halla el perímetro de un rectángulo con vértices en A (1, 6), B (1, 2), C (4, 2) y D (4, 6).
Solución:
Empecemos por dibujar este cuadrilátero en el plano cartesiano.
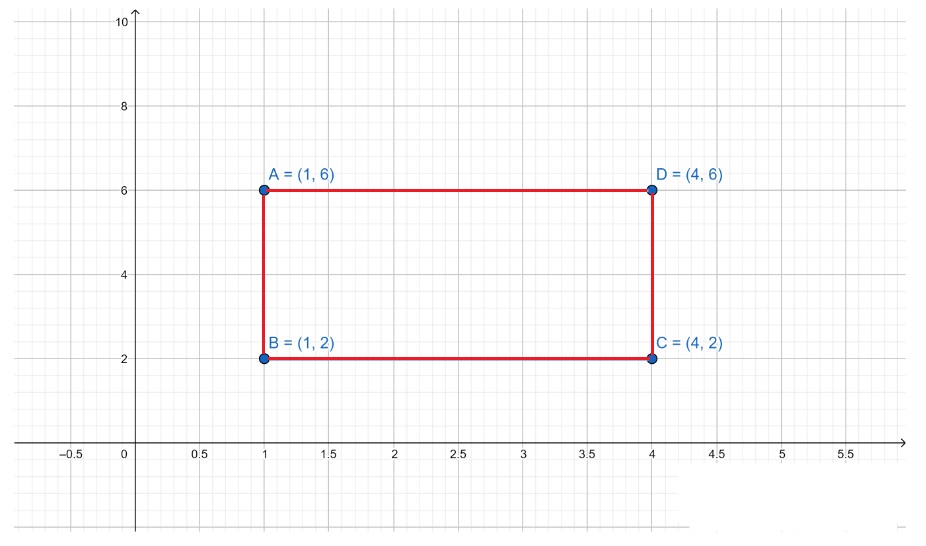
Como tenemos un rectángulo, AB = DC y AD = BC. Por tanto, podemos utilizar la fórmula de la distancia para las longitudes de AB y AD.
Distancia AB, A (1, 6) y B (1, 2)
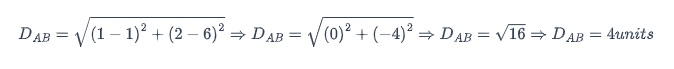
Distancia AD, A (1, 6) y D (4, 6)
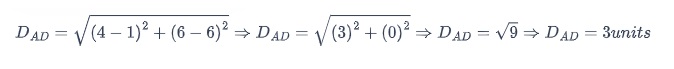
Perímetro ABCD
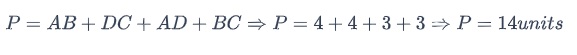
2.3. Área de los cuadriláteros
El área de un cuadrilátero viene descrita por el espacio interior delimitado por su contorno. Cada uno de los seis tipos de cuadriláteros que hemos mencionado anteriormente tiene su propia fórmula del área.
PARALELOGRAMO

Ejemplo 1:
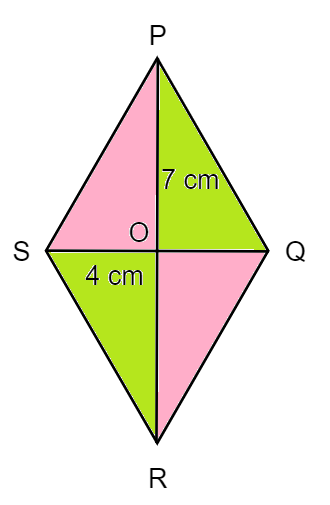
Calcule el área del rombo de abajo dado que PO = 7 cm y SO= 4 cm. El punto O es el punto en el que las dos diagonales PR y SQ se bisecan perpendicularmente.
Solución:
Recuerda: Necesitamos las medidas de las diagonales PR y SQ, del rombo para calcular su área. Como las diagonales de un rombo son perpendiculares y se bisecan entre sí, nos encontramos con que
PO = OR y SO = OQ y, por tanto,
PR=PO+OR =2PO SQ= SO + OQ = 2SO
Resolviendo esto, lo conseguiremos
PR=2(7)=14cm SQ=2(4)=8cm
Por tanto, la diagonal vertical PR mide 14 cm y la diagonal horizontal SQ mide 8 cm. Por la fórmula del área de un rombo,
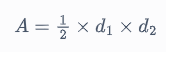
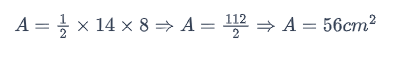
Por tanto, el área de este rombo es de 56 cm2.
Ejemplo 2:
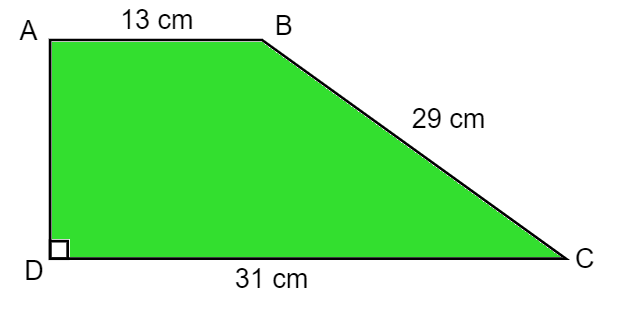
¿Cuál es la altura del trapecio de abajo dado que su área es de ¿330cm2?
Solución
Como AB es paralelo a DC, las bases de este trapecio vienen dadas por AB = 13 cm y DC = 31 cm. La altura viene dada por AD. Por la fórmula del área de un trapecio, obtenemos:
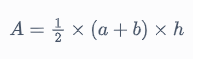
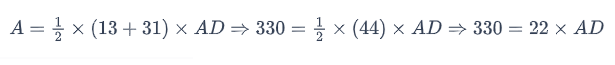
Reordenando y simplificando nuestra expresión, obtenemos:
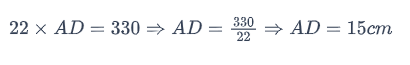
Por tanto, la altura de este trapecio, AD, es de 15 centímetros.
Cálculo del área de cuadriláteros en el plano
Para encontrar el área de un cuadrilátero representado por un conjunto de puntos en el sistema de coordenadas cartesianas, utilizaríamos simplemente la misma técnica que en el caso del perímetro. Sí, aquí también se aplica la fórmula de la distancia. Sin embargo, aquí debemos tener cuidado, ya que hay algunas fórmulas de área que no incluyen los lados de un cuadrilátero dado, sino su altura diagonal o perpendicular; como el paralelogramo, el trapecio, el rombo y la cometa.
Ejemplo 3:
Halla el área de una cometa con vértices en A(0, 4), B(1, 2), C(0, -4) y D(-1, 2).
Solución
Empecemos por dibujar este cuadrilátero en el plano cartesiano.
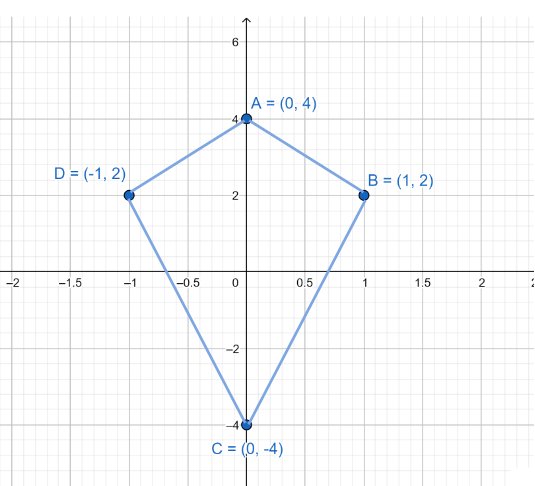
Distancia AC, A (0, 4) y C (0, -4)
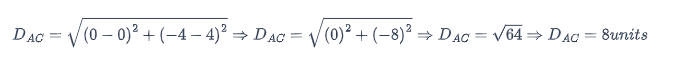
Distancia BD, B (1, 2) y D (-1, 2)
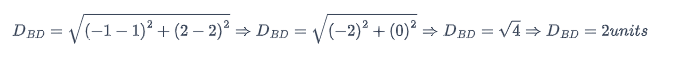
Área A B C D
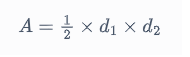
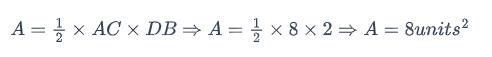
Actividad 2: (Responde en el cuaderno)
1. Di el área y el perímetro de este rectángulo:
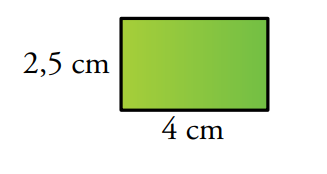
2. ¿Cuál es el lado de este cuadrado cuya área conocemos? ¿Y su perímetro?
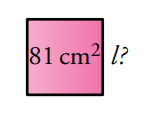
3. Halla el área y el perímetro de este paralelogramo:
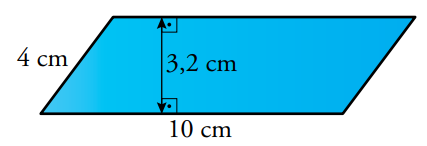
4. Calcula el perímetro y el área de un salón rectangular de dimensiones 6,4 m y 3,5 m.
5. Mide las dimensiones de una página de este libro. ¿Cuántos metros cuadrados de papel se necesitan para hacer el libro completo, sin contar las tapas?

Nota: El libro mide 22,5 cm de ancho por 29 cm de alto. Además, sin contar las tapas, el libro tiene 288 páginas. Como se imprime por las dos caras del papel, en realidad tenemos 144 hojas.
6. Halla el área y el perímetro de las siguientes figuras:

7. Elena tiene un hijo que va a la escuela, de la casa a la escuela hay 1000 m. Esa, también, es la distancia entre la Biblioteca Pública y el Banco. El jueves va por su hijo a la escuela, pero, después irán a la Biblioteca Pública, que queda a 500 m de la escuela. Al salir de la Biblioteca deben ir al Banco, para luego ir a la casa. La disposición de tales edificios es así:
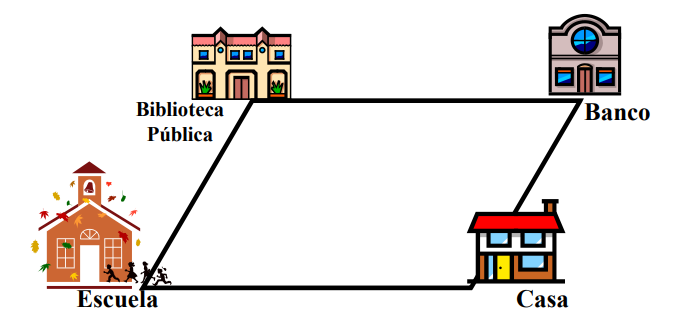
El camino que Elena va a recorrer tiene forma de un cuadrilátero, ¿cómo se llama ese cuadrilátero? Calcule el perímetro del cuadrilátero descrito.
CÍRCULOS
Un círculo representa un conjunto de puntos, todos ellos a una misma distancia de un punto específico. Este punto se llama centro
1. Elementos del círculo
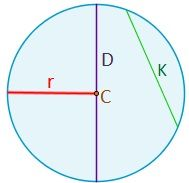
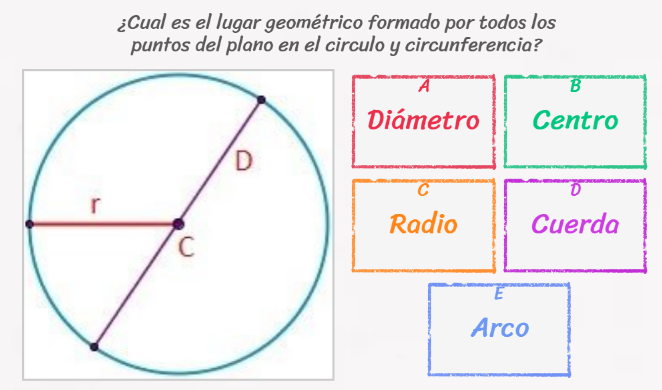
- Centro: el centro C es un punto fijo interior, equidistante de su perímetro (o circunferencia) a una distancia igual al radio.
- Radio: es el segmento r que une el centro ( C ) del círculo con cualquier punto del perímetro de éste.
- Diámetro: segmento D que une dos puntos del perímetro del círculo pasando por el centro ( C ). Su longitud es el doble que la de la radio.
- Cuerda: es un segmento K que une dos puntos del perímetro del círculo sin pasar por el centro.
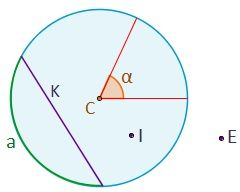
- Arco: es la parte del perímetro del círculo ( a ) que queda entre los dos extremos de una cuerda.
- Punto interior: punto que pertenece al círculo ( I ), encontrándose a una distancia del centro menor o igual quea.
- Punto exterior: puntos que están fuera del círculo ( E ), es decir, a una distancia del centro mayor que a.
- Angulo central: es el ángulo comprendido entre dos segmentos (o radios) que van del centro a dos puntos del perímetro del círculo (α). Un ángulo central determina un arco.
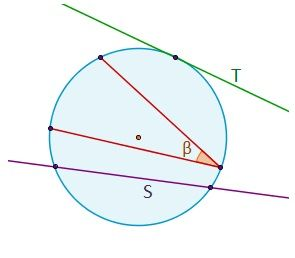
- Tangente: es una recta (T) con un único punto común con el perímetro del círculo. El radio es perpendicular a la tangente en el punto de tangencia.
- Secante: es una recta (S) que corta el perímetro del círculo en dos puntos.
- Ángulo inscrito: ángulo (β) que forman dos cuerdas que coinciden en un mismo punto de la circunferencia. Es decir, es el ángulo que generan tres puntos de ésta.
2. Partes del círculo:
En la superficie del círculo se pueden formar las siguientes partes o figuras circulares:
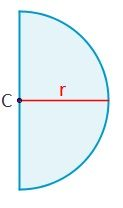
A. Un semicírculo es la superficie del círculo comprendida entre la mitad de una circunferencia y delimitado por su diámetro. El semicírculo es medio círculo.
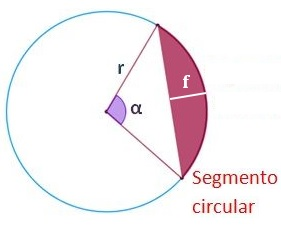
B. El segmento circular (o segmento de un círculo) es la parte del círculo delimitado por un arco del mismo y su cuerda. Un segmento circular cuyo ángulo sea de 180° es un semicírculo.
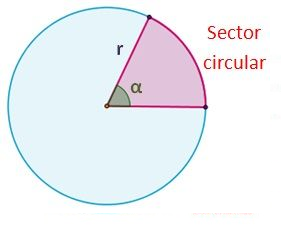
C. Un sector circular es la parte del círculo comprendida entre dos radios y el arco que delimitan
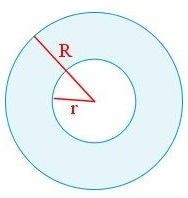
D. La corona circular (o anillo circular) es la superficie del círculo comprendida entre dos circunferencias concéntricas
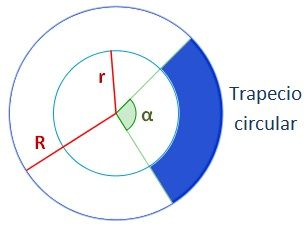
E. Un trapecio circular es la parte de una corona circular comprendida entre dos radios del círculo mayor.
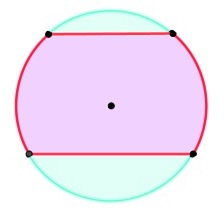
F. Zona circular es la parte de la superficie circular comprendida entre dos cuerdas paralelas
JUEGA: Te invito a que practiques jugando sobre las partes de una circunferencia:
https://wordwall.net/es/resource/5015617/elementos-de-la-circunferencia-y-el-circulo
3. Perímetro de un círculo
¿Sabías que el famoso número pi (π), (la relación entre la longitud de una circunferencia y su diámetro), ya tenía una aproximación de cinco decimales en la Babilonia del siglo XX antes de J. C.
Los matemáticos griegos intentaban resolver la cuadratura del círculo (construir un cuadrado cuya área sea igual a la de un círculo dado).
En la misma época, Arquímedes, a base de dos polígonos regulares de 96 lados, uno inscrito y otro circunscrito, llega a un valor de π = 22/7 (3,1428571428571428571428571428571), aproximación muy importante para su época.
Después, muchos matemáticos han buscado el valor de π, hasta que Lambert, en 1768, demuestra que π es un número irracional y en 1882, Lindemann demuestra la imposibilidad de la cuadratura del círculo.
Con la utilización de potentes ordenadores se ha llegado hasta 206 millones de decimales.
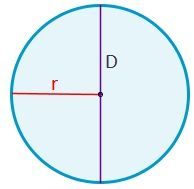
El perímetro de un círculo es el doble del producto de π por el radio (r). También se puede calcular a partir del diámetro (D), siendo el producto de π y el diámetro.
El perímetro del círculo es una circunferencia.

Ejemplo 1:
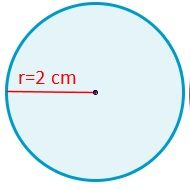
Sea un círculo de radio conocido, siendo éste r =2 cm.
Obtendremos el perímetro a partir del radio:
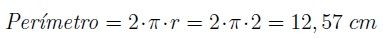
Y se obtiene que el perímetro de un círculo de radio 2 cm es de 12,57 cm.
Ejemplo 2:
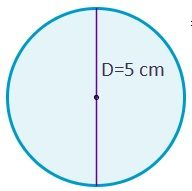
Supongamos que tenemos un círculo de diámetro conocido, siendo D=5 cm.
¿Cuál es su perímetro?
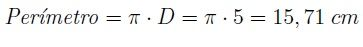
Este círculo de diámetro 5 cm tiene un perímetro de 15,71 cm.
Ejemplo 3:
Un ciclista participa en una competición con bicicleta con rueda lenticular trasera de 622 mm ø.
¿Cuántas vueltas habrá dado la rueda trasera de la bicicleta cuando el ciclista haya corrido 2 km?
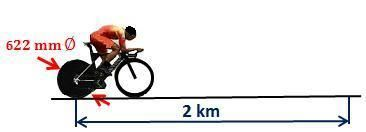
En primer lugar, calcularemos la distancia que recorre la bicicleta cuando la rueda trasera da una vuelta completa, que no es otra cosa que el diámetro de esa rueda lenticular (o sea, el perímetro del círculo).
Perímetro = π · D = π · 0,622 = 1,954 m
Dividiremos la distancia de 2 km, que son 2000 m entre 1,954 m y tendremos:
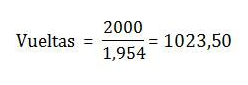
La rueda trasera habrá dado 1.023,50 vueltas.
4. Área del círculo
El área del círculo es igual al producto de π por el radio (r) al cuadrado.
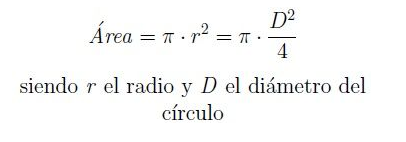
También se puede calcular el área conociendo el diámetro del círculo (D), ya que éste es el doble del radio.
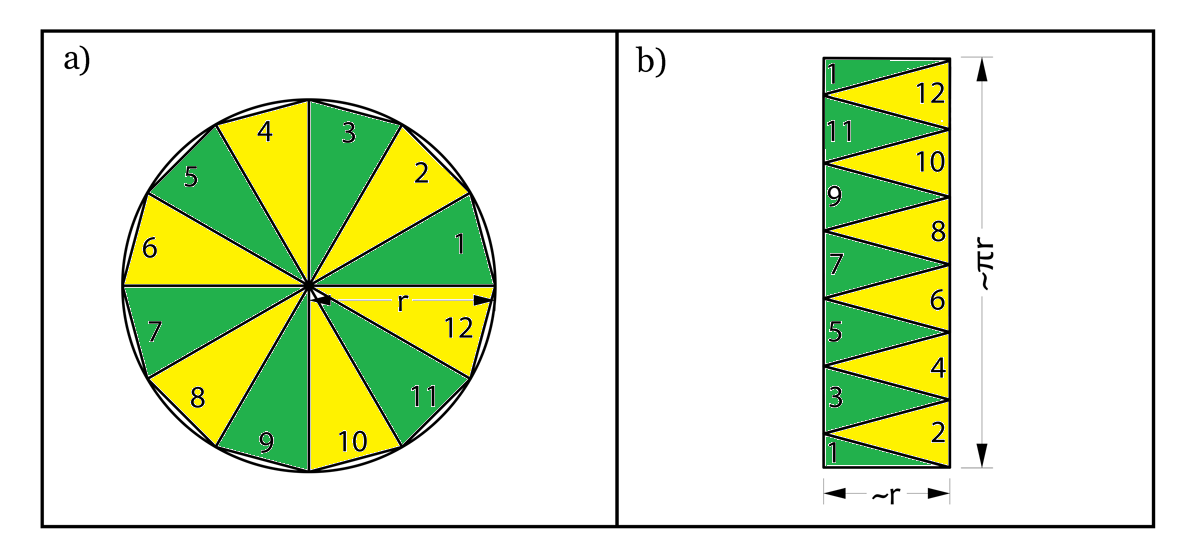
Como un círculo es un polígono regular de infinitos lados, podemos aplicar la fórmula general del área del polígono regular:
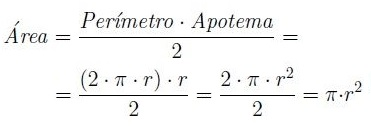
Ejemplo: Hallar el área de un círculo de radio conocido, siendo éste r=2 cm.
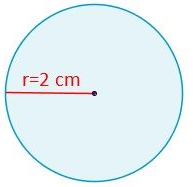
Resolviendo el problema encontramos:
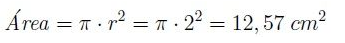
Y se obtiene que el área de un círculo de radio 2 cm es de 12,57 cm2.
Para reforzar más el tema, te invito a observar el siguiente video:
NOTA: Qué diferencia hay entre un círculo y una circunferencia? La diferencia entre un círculo y una circunferencia es que la circunferencia es la línea que rodea al círculo, mientras que el círculo es la superficie que contiene la circunferencia
Actividad 1
1. Calcula el perímetro de cada círculo. Luego, responde en el cuaderno.
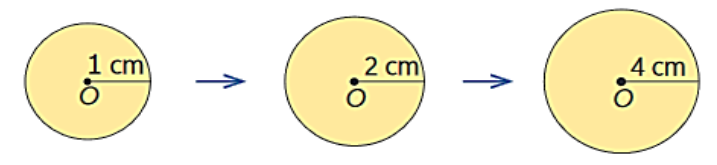
a) ¿A medida que el radio de la circunferencia se duplica, ¿qué ocurre con el perímetro?
b) ¿Cuánto debiese medir el perímetro de un círculo cuyo radio mide 8 cm? Justifica.
2. Calcula el área de cada círculo (realiza los ejercicios en tu cuaderno)
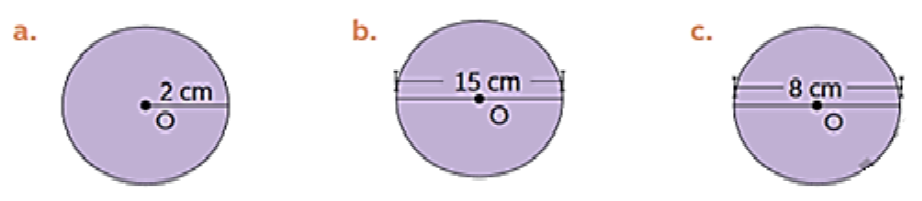
3. ¿cuánto mide el área de la parte pintada, si los radios son 5cm y 3 cm respectivamente? (considere 𝜋 = 3,14)
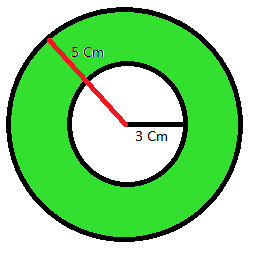
4. La piscina circular se encuentra en un terreno cuadrado, cuyo perímetro mide 16 m2 ¿Cuánto mide el perímetro de la piscina?

5. Lily tiene que calcular el diámetro de la circunferencia. La profesora solo le dijo que el perímetro es 43,96 cm y que considerara 𝜋 = 3,14. Piensa y piensa y no sabe qué hacer. ¿Cómo resolverías tú el ejercicio que le dieron a Lily?
6. ¿Qué uso o usos le darías al cálculo del área de un círculo en tu vida cotidiana?
7. ¿Pediste ayuda para desarrollar la actividad? ¿a quién? Si no lo hiciste, explica por qué.
8. Para recuperar puntos te invito a desarrollar los ejercicios en línea jugando:
https://www.cerebriti.com/juegos-de-matematicas/area-y-perimetro-del-circulo
9. para el siguiente ejercicio trata de no utilizar calculadora. Realiza los ejercicios en tu cuaderno o en una hoja, o en su defecto el docente hará una competencia del que termine primero el ejercicio.
https://es.educaplay.com/recursos-educativos/3214655-perimetro_y_area_del_circulo.html
HETEROEVALUACIÓN:
La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad: