Grado 11 - Cálculo
Periodo 2


DBA 3. Utiliza instrumentos, unidades de medida, sus relaciones y la noción de derivada como razón de cambio, para resolver problemas, estimar cantidades y juzgar la pertinencia de las soluciones de acuerdo con el contexto.

ESTANDAR BÁSICO DE COMPETENCIA: Analizo las relaciones y propiedades entre las expresiones algebraicas y las gráficas de funciones.
TEMAS:
1. Defina el concepto de relación y función. 2. Notación y representación de funciones. 3. Conoce las propiedades de las funciones. 4. Clasifica los diferentes tipos de funciones, por su gráfica y ecuación. 5. Operaciones entre funciones
SABERES PREVIOS

1. EXPRESIONES ALGEBRAICAS
Una expresión algebraica es una combinación de números (constantes y coeficientes), variables (letras) y operaciones matemáticas (+, -, ×, ÷, potenciación) que se utiliza para representar cantidades y relaciones. Estas combinaciones pueden contener un solo término (monomio) o varios, conectados por sumas y restas.
Acá te dejo un video para que refresques la memoria
2. BINOMIO CUADRADO
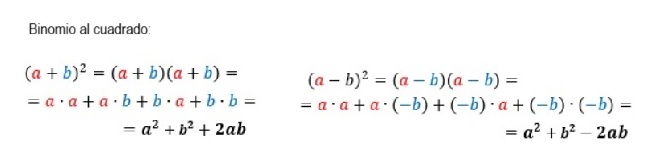
3. PENDIENTE DE UNA RECTA A PARTIR DE DOS PUNTOS
4. GRÁFICA DE LA RECTA: PENDIENTE-ORDENADA AL ORIGEN (y=mx+b)
5. FUNCIONES PARES E IMPARES
6. FUNCIÓN LOGARÍTMICA
De la misma manera que la radicación, la logaritmación es una operación inversa a la potenciación. Esta operación permite hallar el exponente cuando se conoce la base y la potencia.
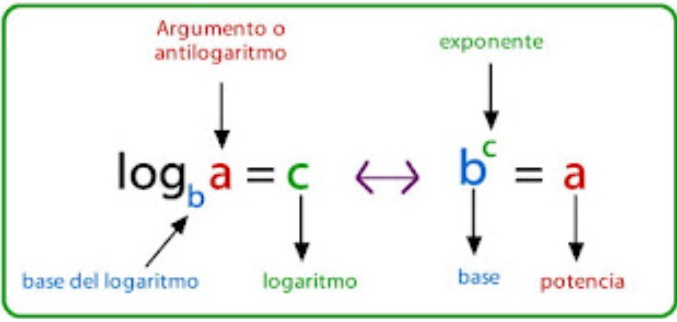
La expresión log𝑎 𝑏 = 𝑛 se lee "logaritmo en base a de b es igual a n"
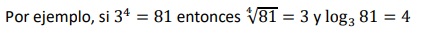
Actividad 1. Practica estos ejercicios:
EJERCICIOS DE EXPRESIONES ALGEBRAICAS
Ejercicio 1.- Expresa en lenguaje algebraico cada uno de los siguientes enunciados:
a. El 30% de un número.
b. El área de un rectángulo de base 3 cm y altura desconocida.
c. El perímetro de un rectángulo de base 3 cm y altura desconocida.
d. El doble del resultado de sumarle a un número entero su siguiente.
Ejercicio 2.- Traduce al lenguaje algebraico las siguientes expresiones:
a. El triple del resultado de sumar un número con su inverso.
b. El doble de la edad que tendré dentro de cinco años.
c. El quíntuplo del área de un cuadrado de lado x.
d. El área de un triángulo del que se sabe que su base es la mitad de su altura.
Ejercicio 3.- Expresa en lenguaje algebraico:
a. La mitad del resultado de sumarle 3 a un número.
b. La tercera parte del área de un rectángulo en el que la base mide el doble que la altura.
c. El cuadrado de la suma de dos números enteros consecutivos.
d. La media de un número y su cuádruplo.
Ejercicio 4.- Traduce al lenguaje algebraico cada uno de estos enunciados:
a. La cuarta parte de un número entero más el cuadrado de su siguiente.
b. El perímetro de un triángulo isósceles del que sabemos que su lado desigual mide 4 cm menos que cada uno de los dos lados iguales.
c. La diagonal de un cuadrado de lado x.
d. El doble de la edad que tenía hace 7 años.
Ejercicio 5.- Traduce al lenguaje algebraico:
a. La suma de un número con el doble de otro.
b. El precio de una camisa rebajado en un 20%.
c. El área de un círculo de radio x.
d. La suma de tres números enteros consecutivos.
EJERCICIOS DE SIMETRÍA:
Ejercicio 6.- Determina si las siguientes funciones son simétricas o no:
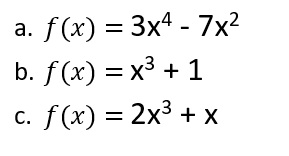
EJERCICIOS BINOMIO CUADRADO:
Ejercicio 7.- Realiza los siguientes ejercicios

PENDIENTE DE UNA RECTA A PARTIR DE DOS PUNTOS:
Ejercicio 8.- Realiza el ejercicio interactivo en el siguiente enlace:
GRÁFICA DE LA RECTA: PENDIENTE-ORDENADA AL ORIGEN (y=mx+b)
Ejercicio nº 9.- Grafica la siguiente recta de acuerdo a su función
y = 2x + 7
I. RELACIÓN - RANGO - FUNCIÓN
CONCEPTO:
Relación es la correspondencia de un primer conjunto, llamado Dominio , con un segundo conjunto, llamado Recorrido o Rango , de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango. Por su parte, una Función es una relación a la cual se añade la condición de que a cada valor del Dominio le corresponde uno y sólo un valor del Recorrido, en otras palabras una función es una regla que asocia elementos de un conjunto con elementos de otro conjunto, de modo que elemento del primer conjunto se asocia con uno y sólo un elemento del segundo conjunto.
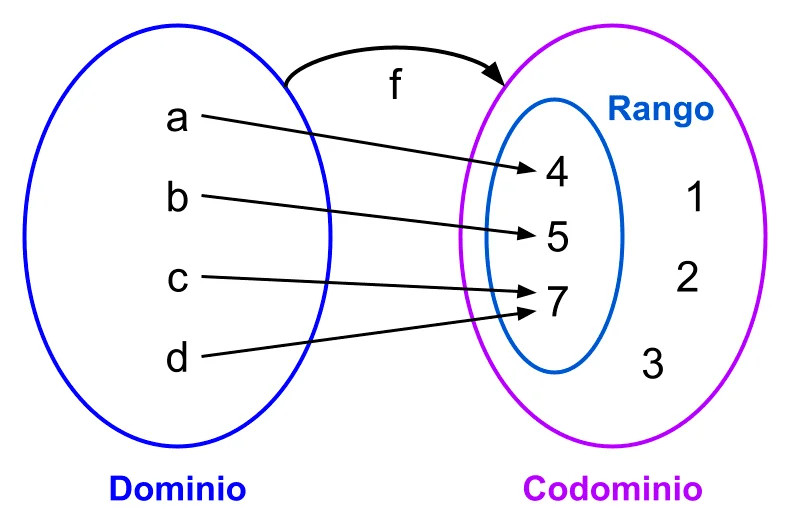
Si (a,b) Ɛ f y (a,c) Ɛ f => b = c
El concepto de relación implica la idea de correspondencia entre los elementos de dos conjuntos que forman parejas ordenadas. Cuando se formula una expresión que liga dos o más objetos entre sí, postulamos una relación (no necesariamente matemática).
Ejemplo 1: Samuel es padre de Irma. (Samuel, Irma)
Del ejemplo anterior podríamos decir matemáticamente que: S ---> I Relación: Es padre
Se llama relación entre los conjuntos A y B a un subconjunto del producto cartesiano A x B. Este puede estar formado por un solo par ordenado, varios o todos los que forman parte de A x B. Si establecemos una relación entre los elementos de un mismo conjunto
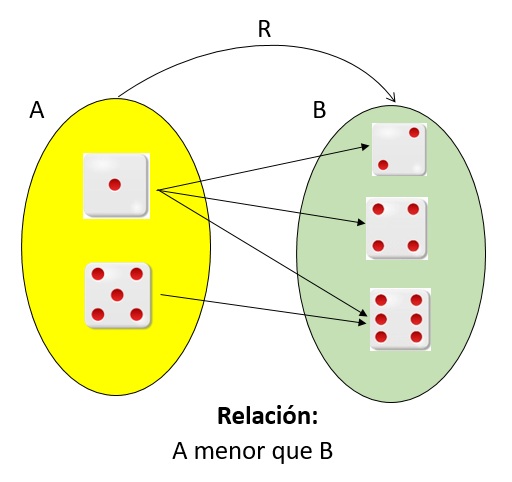
Ejemplo 2
Sea A = {1, 2, 3, 4}
B = {4, 5, 6, 7, 8}
R la relación definida de A en B determinada por la regla "y es el doble de x" o "y = 2x", encontrar dominio y rango de la relación.
Solución: El total de pares ordenados que podemos formar, o producto cartesiano es:
A x B = {(1, 4), (1, 5), (1, 6), (1, 7), (1, 8), (2, 4), (2, 5), (2, 6), (2, 7), (2, 8), (3, 4), (3, 5), (3, 6), (3, 7), (3, 8), (4, 4), (4, 5), (4, 6), (4, 7), (4, 8)}
Pero los pares que pertenecen a la relación R (y = 2x) son solo: R = {(2, 4), (3, 6), (4, 8)}
En esta relación vemos que: "4 es el doble de 2"; esto es, "4 es la imagen de 2 bajo R", dicho de otro modo, "2 es pre imagen de 4".
Así, el dominio y rango para el ejercicio es:
Dominio = {2, 3, 4} Rango = {4, 6, 8}
Según lo que vemos, ¿Qué relación hay entre el Dominio y el conjunto de partida?
A = {1, 2, 3, 4}
B = {4, 5, 6, 7, 8}
En el Dominio falta el elemento 1 del conjunto de partida (verifica los datos de A), por lo tanto el Dominio es un subconjunto de A.
Otra pregunta: ¿Todo elemento del conjunto de llegada es elemento del rango? La respuesta es no, pues en el rango faltan el 5 y el 7 (Verifica los datos de B).
Resumiendo:
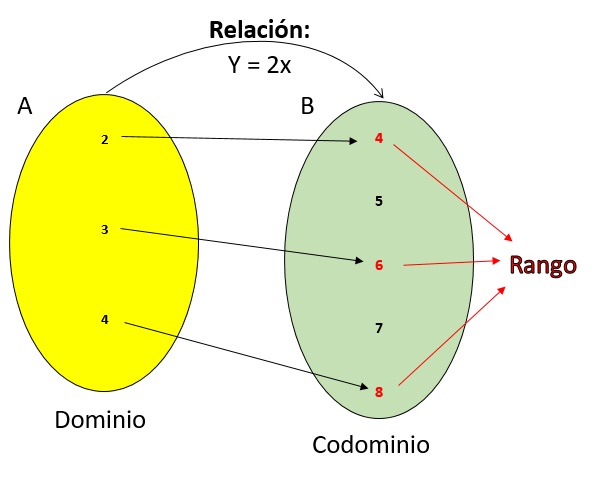
- El conjunto A, es el conjunto inicial
- El conjunto B, es el conjunto final
- El Dominio es {2,3,4)
- El Rango es {4,6,8}
- El codominio es el conjunto B
- La relación es (y = 2x)
FORMAS DE DEFINIR UNA FUNCION
Las funciones se pueden determinar de varias formas:
1. Tabla de valores: es una representación de datos, mediante pares ordenados que expresan la relación entre dos variables.
2. Expresión analítica de una función: es una ecuación que relaciona algebraicamente las variables que intervienen.
3. Gráfica: es un dibujo o boceto que permite conocer intuitivamente el comportamiento de dicha función.
Acá damos un ejemplo con las tres características:
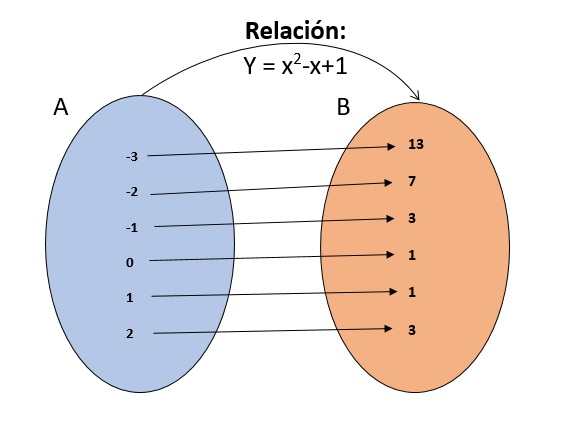
Ejemplo. La relación o expresión analítica: A cada número le corresponde elevarlo al cuadrado menos el mismo número más uno
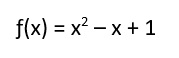
Es una función que está expresada mediante su expresión analítica. Para trazar su gráfica, puede construirse una tabla de valores.
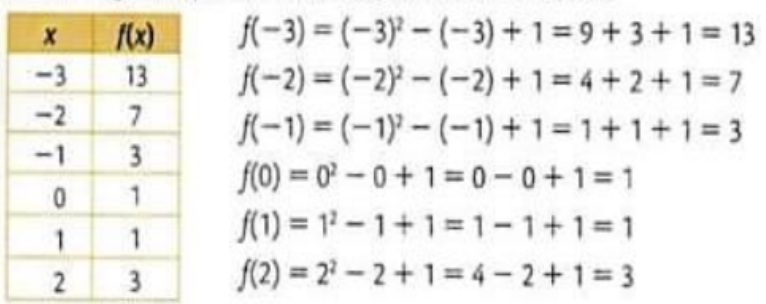
Al representar las parejas ordenadas (-3,13), (-2,7), (-1,3), (0,1), (1,1), (2,3) y unirlas mediante un trazo, se obtiene la representación gráfica de la función f(x):
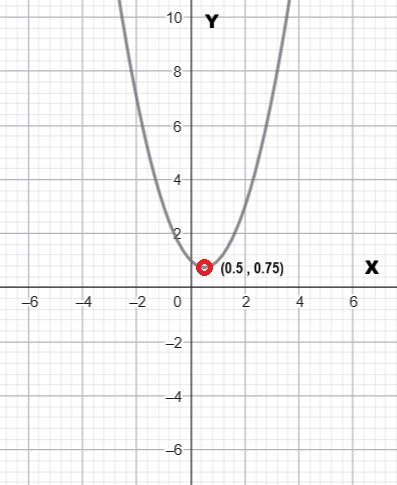
A partir de la gráfica de la función f(x) es posible determinar su dominio y recorrido.
Puesto que X puede tomar cualquier valor real D(f) = R (Dominio de la función es un real).
De otro lado Y toma valores mayor o igual a 1/2;
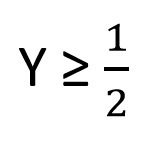
La relación de la función sería la siguiente:
Si te quedó dificil entender el tema, te invito a observar el siguiente video:
Actividad 2. Elabora en tu cuaderno los siguientes ejercicios:
1. Grafica en tu cuaderno o con la ayuda de Geogebra la función f(x) = 8 y responde:
a. ¿Cuál es el dominio y rango de f?
b. Cómo se escribiría por comprensión el conjunto de valores de f.
c. ¿Cuál es la imagen para x = 5?
d. ¿Pertenece al dominio el número 7?
e. ¿Pertenece al rango el valor y = 4?
f. ¿Qué se puede afirmar acerca del crecimiento o decrecimiento de la función?
g. ¿Las funciones constantes son funciones continuas? ¿por qué?
2. Grafica la función determinada por la expresión:
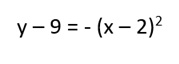
y determina (Nota, tienes que desarrollar utilizando binomio cuadrado):
a. Su vértice e intercepto con los ejes.
b. Dominio y Codominio.
c. Rango teniendo en cuenta su vértice.
d. Intervalos de crecimiento y decrecimiento
e. ¿Su vértice es un valor máximo o un valor mínimo de la función?
f. Paridad
g. Continuidad
h. ¿Es una parábola que abre hacia arriba o hacia abajo?
3. La recta pasa por los puntos 𝑃1(2,4) 𝑦 𝑃2(−3,4), entonces la pendiente de la recta es
A. 𝑚 = 0
B. 𝑚 = −1
C. 𝑚 = 1
D. 𝑚 = 6
4. Observa el siguiente gráfico:
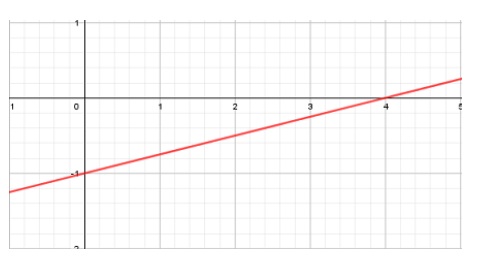
El intercepto en el eje y corresponde a:
A. 𝑥 = 4
B. 𝑥 = −1
C. 𝑦 = 4
D. 𝑦 = −1
5. Observa el siguiente gráfico:
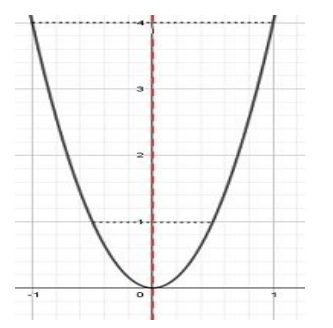
La ecuación que representa la gráfica mostrada está dada de la forma:
A. 𝑦 = 𝑚𝑥 + 𝑏
B. 𝑦 = 0
C. 𝑦 = 𝑎𝑥2
D. 𝑦 = −𝑎𝑥2
2. PROPIEDADES DE LAS FUNCIONES
Al analizar una función podemos encontrarnos con una serie de características distintivas. Entre las propiedades de una función tenemos:
- Dominio: es el conjunto de partida que contiene todos los valores para los cuales la función está definida.
- Codominio: es el conjunto de llegada de la función.
- Rango: es el conjunto de todos los valores que la función produce como resultado.
Ejemplos:
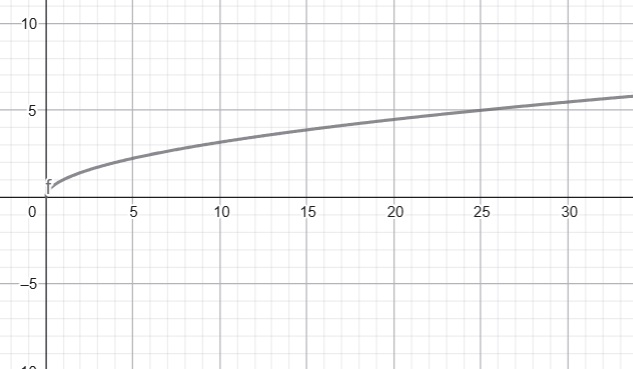
y=√ x
- La función raíz cuadrada y=√ x solo está definida para valores no negativos de x, por lo que su dominio es Df=[0,+∞). El codominio es R. Como la raíz cuadrada arroja un resultado no negativo, el rango de la función es R=[0,+∞).
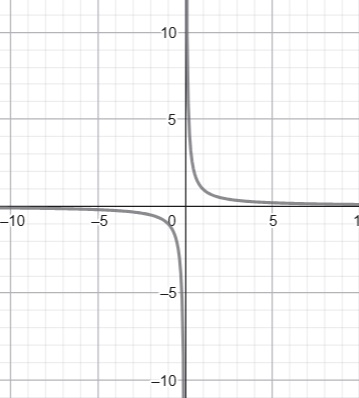
f(x)=1/x
- La función racional f(x)=1/x está definida para todos los números reales excepto el cero, entonces, su dominio es Df=R−{0}. El codominio, como no se especifica, es R (Reales). Como valores de salida tenemos a todos los números reales menos el cero, por lo tanto, su rango es Rf=R−{0}.
4. Signo: describe si la función es positiva o negativa en un intervalo dado. si su gráfica se encuentra por encima del eje x en ese intervalo es positiva y se simboliza como f(x)>0. De forma análoga, la función es negativa en un intervalo si su gráfica se encuentra por debajo del eje x y se denota como f(x)<0. Los valores donde la gráfica corta al eje x son llamados raíces o ceros; en ellos, la función es cero: f(x)=0.
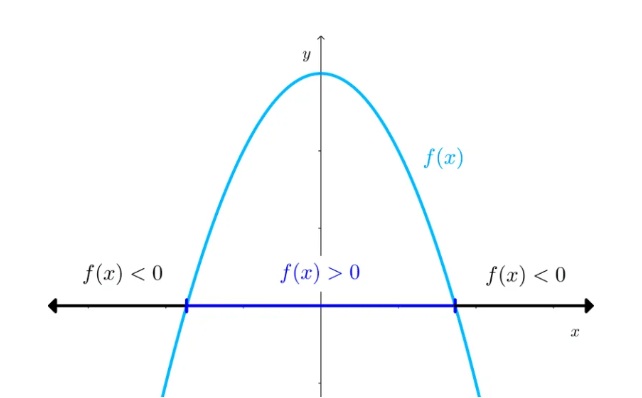
5. Puntos de corte con los ejes: La gráfica de una función puede cortar a los ejes cartesianos. La intersección con el eje x se da cuando y=0, los valores de x que anulan la función se llaman ceros o raíces. La intersección con el eje y se da cuando x=0; si esta intersección existe, es única.
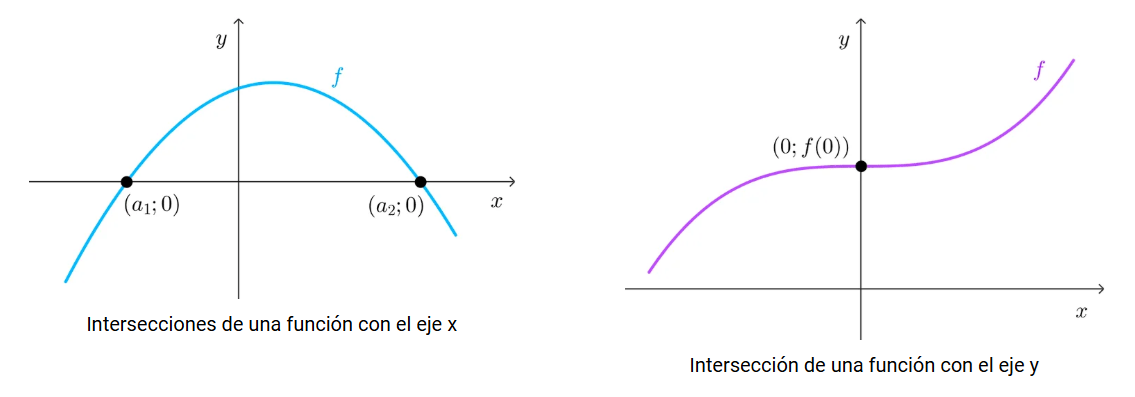
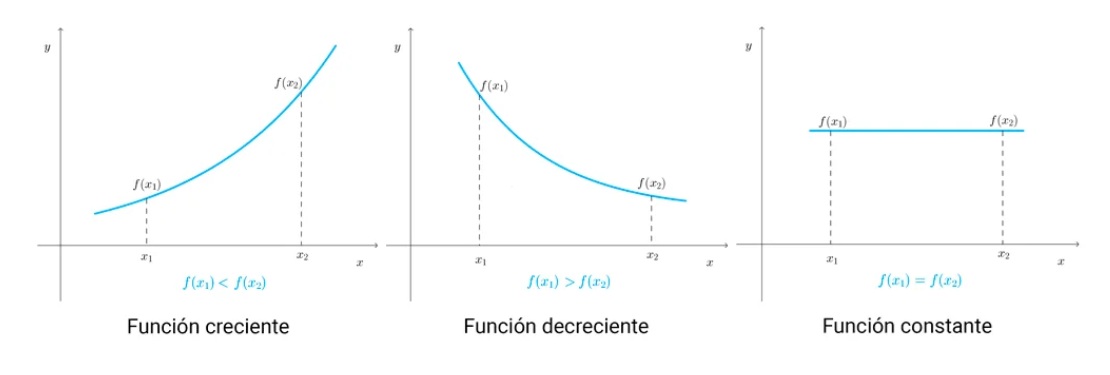
6. Monotonía: describe si la función aumenta, disminuye o permanece constante en un intervalo dado.
Una función es
crecienteen un intervalo si sus valores aumentan a medida que la variable independiente aumenta. Gráficamente, la curva de la función sube de izquierda a derecha.
Una función es
decrecienteen un intervalo si sus valores disminuyen a medida que la variable independiente aumenta. Gráficamente, la curva de la función baja de izquierda a derecha.
Una función es
constanteen un intervalo si sus valores son iguales en cualquier punto del intervalo. Gráficamente, la curva es un segmento de recta paralelo al eje x.
Formalmente, dada una función f y el intervalo I que pertenece a su dominio:
- f es creciente en I si y solo si f(x1)<f(x2) siempre que x1<x2 en I.
- f es decreciente en I si y solo si f(x1)>f(x2) siempre que x1<x2 en I.
- f es constante si f(x1)=f(x2) para todo x1 y x2 en I.
Una función se dice monótona si solo crece o solo decrece en todo su dominio. Si la función tiene intervalos de crecimiento y decrecimiento en su dominio, se dice que es no monótona
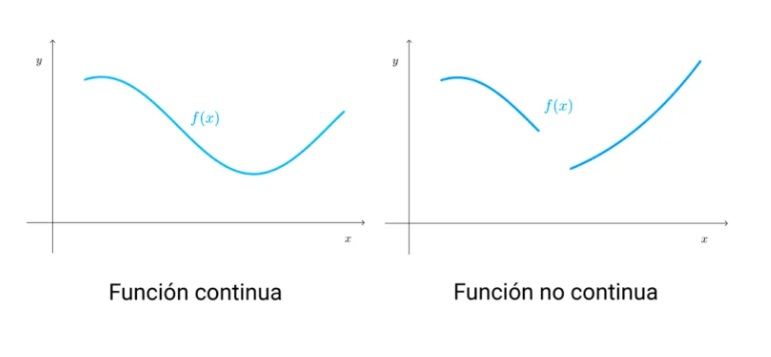
indica si la función podría ser graficada en un solo trazo sin levantar el lápiz del papel. Una función continua es aquella que no presenta "saltos" o "interrupciones" en su gráfica. En otras palabras, podemos dibujar su gráfica sin levantar el lápiz del papel.
Ejemplos
- Las funciones polinómicas (constantes, lineales, cuadráticas, cúbicas, etc.) son continuas en todo su dominio, por tanto, sus gráficas no presentan saltos.
- La función f(x)=∣x∣/xf(x)=∣x∣/x presenta una discontinuidad en x=0 porque su gráfica "salta" de -1 hasta 1.
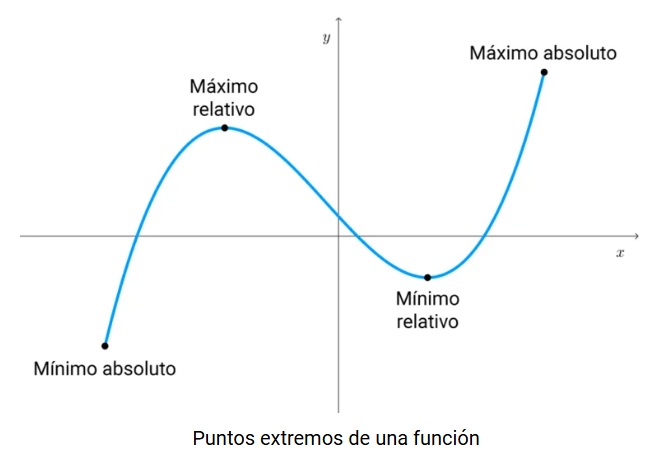
8. Puntos extremos:
Son los valores máximos o mínimos que la función puede tomar. Los puntos extremos de una función son aquellos donde su valor alcanza el valor más grande o más pequeño posible. Estos puntos son importantes para analizar el comportamiento de la función. Existen cuatro tipos de puntos extremos:
- Máximo local o relativo: es un punto donde la función alcanza un valor mayor que todos los valores de la función en un intervalo a su alrededor.
- Mínimo local o relativo: es un punto donde la función alcanza un valor menor que todos los valores de la función en un intervalo a su alrededor.
- Máximo absoluto o global: es el punto donde la función alcanza el valor más grande posible en todo su dominio.
- Mínimo absoluto o global: es el punto donde la función alcanza el valor más pequeño posible en todo su dominio.
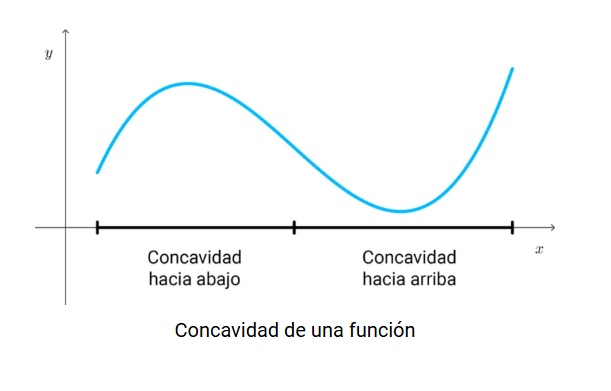
9. Concavidad:
Describe si la gráfica de la función se curva hacia arriba o hacia abajo. La concavidad de una función describe la forma de su gráfica, indicando si se curva hacia arriba o hacia abajo en diferentes intervalos de su dominio. En un intervalo, la función puede ser cóncava hacia arriba (con forma de U) o cóncava hacia abajo (con forma de ∩). Los puntos donde la concavidad cambia se llaman puntos de inflexión.
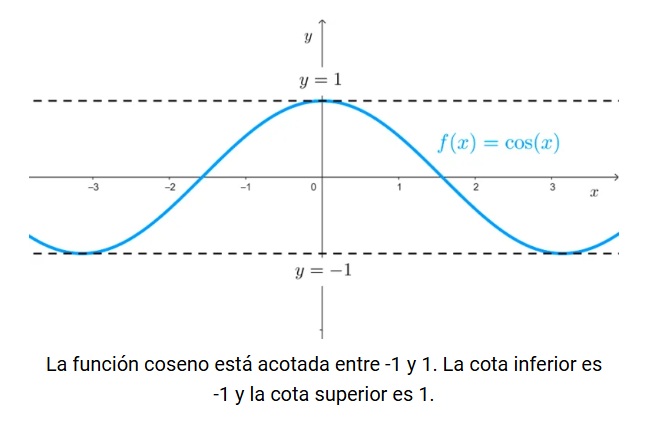
10. Acotación:
Indica si la función está limitada en su crecimiento o decrecimiento por ciertos valores.
Una función está acotada superiormente si existe un valor que las imágenes no superan, y está acotada inferiormente si sus imágenes se mantienen siempre por encima de cierto número. Se dice que una función está acotada si existen esos dos valores.
Formalmente, si f una función definida en un conjunto D, entonces:
- f está acotada superiormente si existe un número real M tal que f(x)≤M para toda x en D. M recibe el nombre de cota superior.
- f está acotada inferiormente si existe un número real m tal que f(x)≥m para toda x en D. El valor m recibe el nombre de cota inferior.
- f es una función acotada si está acotada superior e inferiormente. Se cumple entonces que m≤f(x)≤M.
Ejemplo
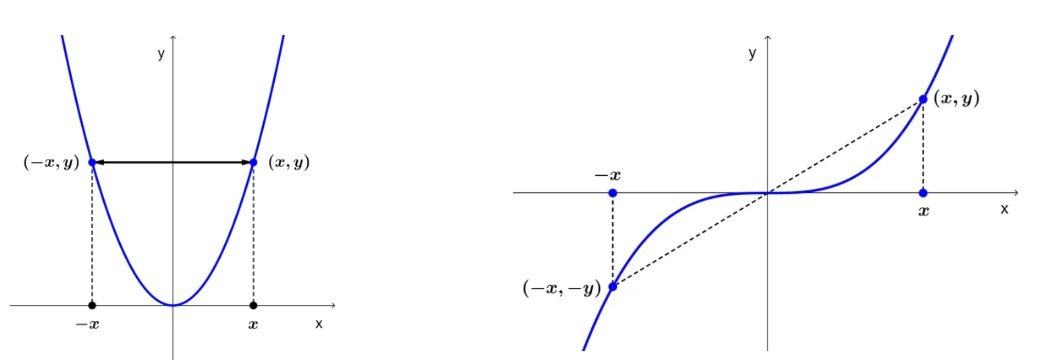
11. Simetría:
Describe si la función exhibe algún tipo de simetría respecto al eje y o al origen de coordenadas.
La simetría de una función se refiere a la propiedad que tiene su gráfica de coincidir consigo misma al ser reflejada respecto a un eje o un punto. Existen dos tipos principales de funciones según su simetría:
- Funciones pares: son aquellas simétricas respecto al eje y.
- Funciones impares: son aquellas simétricas respecto al origen de coordenadas.
12. Periodicidad:
Indica si la función se repite en intervalos regulares.
Las funciones periódicas son aquellas que repiten sus valores en intervalos regulares. Esto significa que para cualquier valor del dominio, la función produce el mismo valor después de cierto intervalo.
Formalmente, una función f es periódica con período T si se cumple que f(x+T)=f(x) para toda x del dominio. El número T es positivo y se llama período de la función. Al valor más pequeño del período se le llama período fundamental.
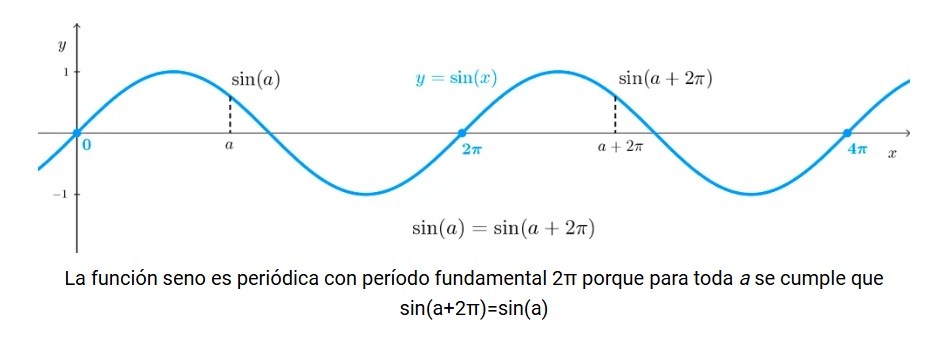
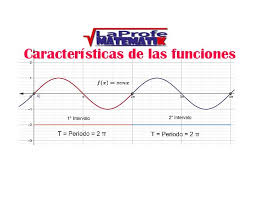
Observa la función Seno (Amplitud, fase y periodo):
13. Comportamientos asintóticos:
Describe si la gráfica de la función se acerca a una recta a medida que la variable independiente se acerca a un valor, aumenta o disminuye sin límites.
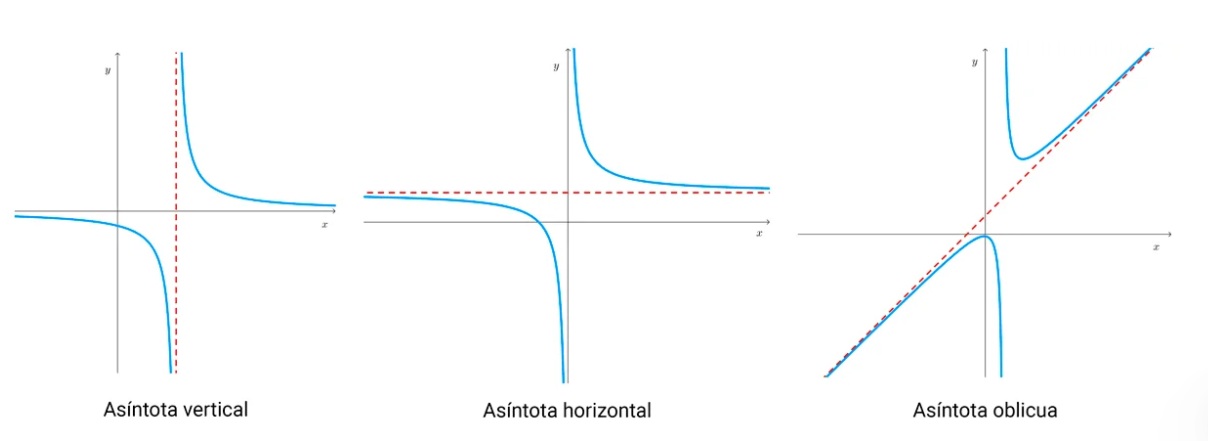
Una asíntota es una recta a la que la gráfica de una función se acerca a medida que el valor de la variable independiente se acerca a un valor específico o se aleja hacia el infinito. Existen tres tipos de asíntotas:
- Asíntotas horizontales: son líneas horizontales a las que la gráfica se acerca cuando la variable independiente tiende a infinito positivo o negativo.
- Asíntotas verticales: son líneas verticales a las que la gráfica se acerca cuando la variable independiente se acerca a un determinado valor.
- Asíntotas oblicuas: son líneas no horizontales ni verticales a las que la gráfica se acerca cuando la variable independiente tiende a infinito positivo o negativo.
La presencia de asíntotas es común en funciones racionales, aunque existen otros tipos de funciones que pueden tenerlas. Existen funciones que no tienen ninguna asíntota.
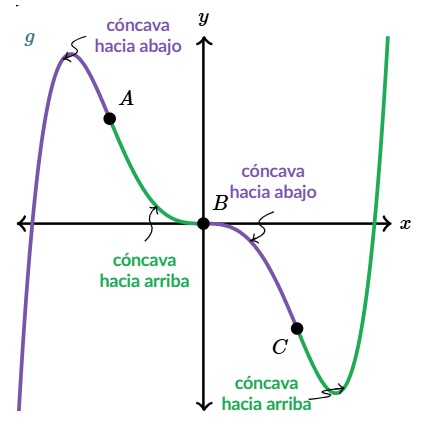
14. Puntos de inflexión:
Los puntos de inflexión son lugares en una curva donde cambia su concavidad (de "U" a "∩", o viceversa), cruciales para entender su forma; matemáticamente, ocurren cuando la segunda derivada es cero o indefinida y cambia de signo, marcando un giro en la tendencia de la función, lo cual es vital en cálculo para el análisis de funciones y en narrativa para momentos críticos que transforman una historia.
Te invito a reforzar más el tema con el siguiente video:
O este otro: https://www.youtube.com/watch?v=YH6H3-d0YUk

Actividad 3.
1) ¿Cuáles de las siguientes relaciones representan funciones?
a) f = {(2,−2),(−3,3),(4,−4),(−5,5)}
b) g = {(5,2),(1,3),(5,4)}
c) F = {(x, y) : |x + 4| − y = 0}
d) G={(x ,y) : ( y-1)2 + (x + 7)2 = 8}
2) ¿Cuáles de las siguientes gráficas representan funciones?
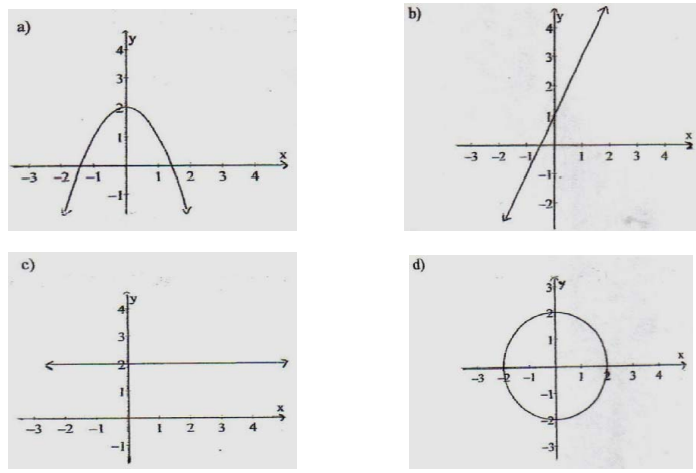
3) ¿Cuáles de las siguientes correspondencias representan funciones?
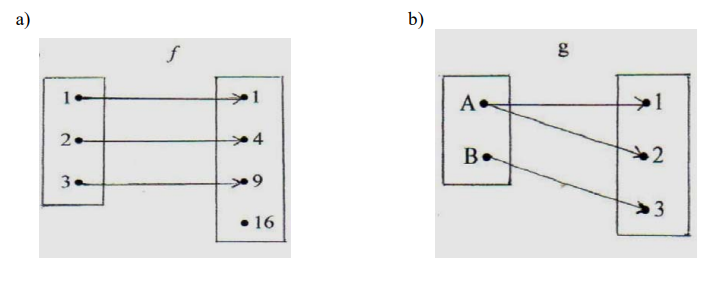
4. Sea:
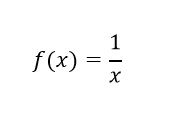
Halla:
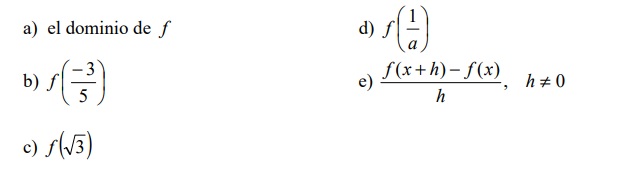
5. Usando la gráfica de la función f que aparece a continuación, halla:
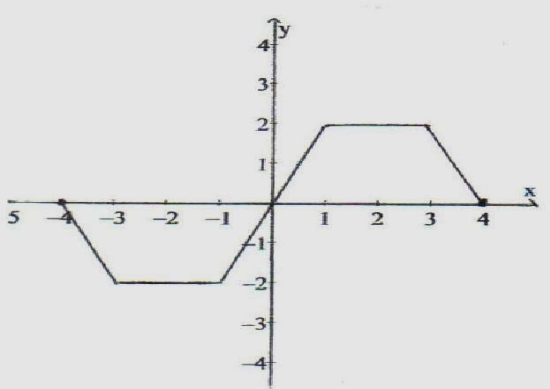
a) dominio i) intervalos donde f es:
b) campo de valores 1) creciente
c) f (0) 2) decreciente
d) f (−2) 3) constante
e) interceptos en el eje de x j) valores de x donde:
f) intercepto en el eje de y 1) f (x) = 2
g) ceros de f 2) f (x) < 0
h) simetría de la gráfica (si la tiene) 3) f (x) ≥ 0
6. Usando la prueba algebraica, determina cuáles de las siguientes funciones son pares, impares o ninguna de las dos:

7. Halla los interceptos en x y el intercepto en y para las siguientes funciones:

8.
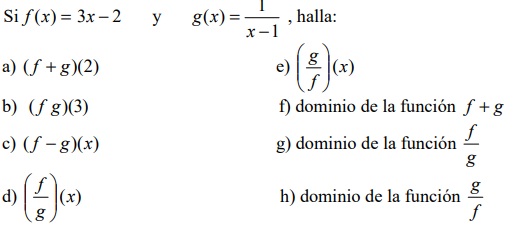
9. Demuestra que una función es la inversa de la otra:
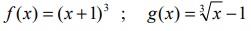
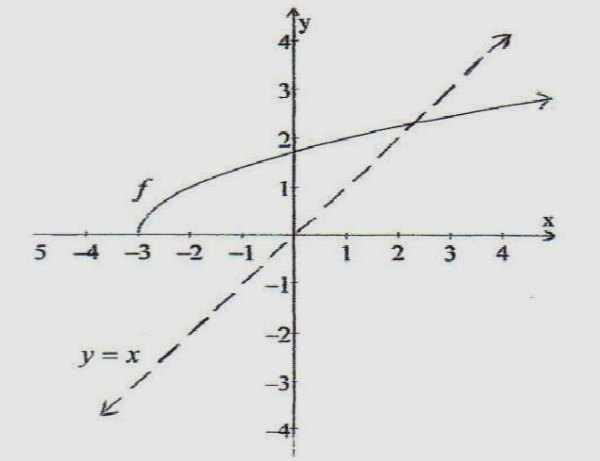
10. La gráfica de la función f aparece a continuación. Traza la gráfica de:
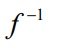
en el mismo sistema cartesiano. Por conveniencia también aparece la gráfica de y = x
11. Desarrolla los ejercicios del siguiente link: https://es.khanacademy.org/math/ap-calculus-ab/ab-diff-analytical-applications-new/ab-5-6a/e/analyze-points-of-inflection-graphical
4. TIPOS DE FUNCIONES
Las funciones algebraicas son:
1. Funciones polinómicas
2. Funciones constantes
3. Funciones polinómicas de primer grado
4. Funciones racionales
5. Funciones radicales
6. Funciones algebraicas a trozos
Las funciones trascendentes son:
1 Funciones exponenciales
2 Funciones logarítmicas
3 Funciones trigonométricas
FUNCIONES ALGEBRAICAS
Las funciones algebraicas pueden ser:
Funciones explícitas
Si se pueden obtener las imágenes de X por simple sustitución como en este ejemplo: f(x)=5x-2
Funciones implícitas
Si no se pueden obtener las imágenes de X por simple sustitución, sino que es necesario efectuar operaciones, como en este ejemplo 5X -Y - 2 = 0
Ademas, de esta clasificación existen 6 tipos de funciones algebraicas
1. FUNCIONES POLINÓMICAS:
Son las funciones que vienen definidas por un polinomio.
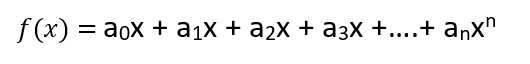
Su dominio es R, es decir, cualquier número real tiene imagen. Ej:
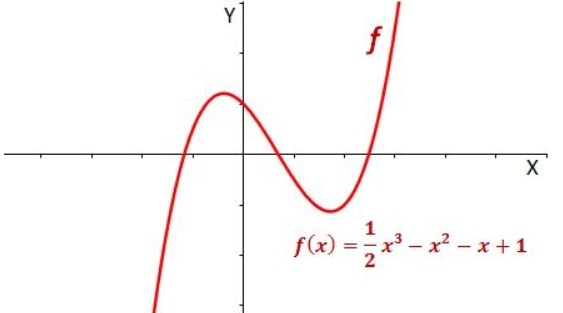
PROPIEDADES DE LA FUNCIONES POLINÓMICAS:
Sean f(x) y g(x) dos funciones polinómicas, entonces:
- La gráfica de una función polinómica corta al eje Y en (0, a0).
- Corta al eje X un número de veces igual o inferior al grado del polinomio n.
- El número de máximos y mínimos relativos de una función polinómica es, como mucho, el grado del polinomio menos 1 (n – 1).
- En las funciones polinómicas no existen asíntotas.
- El número de puntos de inflexión es igual o menor a n – 2.
- Si el grado de todos los términos fuese impar, la gráfica sería simétrica respecto al origen de coordenada (al doblar la hoja sobre el eje Y la figura se sobrepone). Pero si todos los términos tuviesen grado par, la gráfica sería simétrica respecto al eje Y (al doblar la hoja sobre el eje Y y luego sobre la X la figura se sobrepone) .
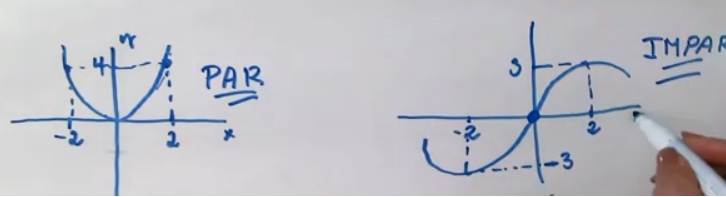
- En la gráfica de una función polinómica, la rama de la derecha será creciente cuando el coeficiente del término de mayor grado, an, sea positivo. Y esa rama será decreciente cuando an sea negativo.
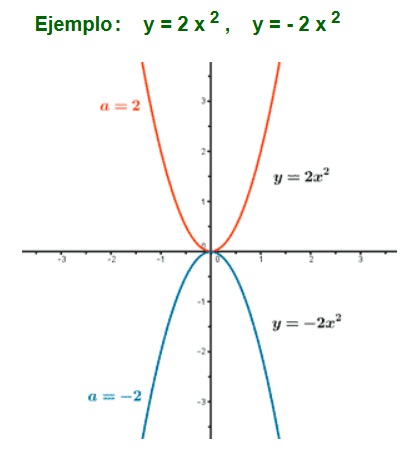
- En la gráfica, la rama de la izquierda será decreciente cuando se cumpla que el grado del polinomio n sea par y el coeficiente del término de mayor grado, an, sea negativo. También será decreciente la rama izquierda cuando n sea impar y, al mismo tiempo, an sea positivo. En el resto de los casos, la rama izquierda será siempre creciente (irá creciendo hacia arriba).
- La suma de dos funciones polinómicas es una función polinómica. Es decir:f(x)+g(x) es polinómica
2. FUNCIONES CONSTANTES:
El criterio viene dado por un número real.
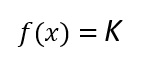
La gráfica es una recta horizontal paralela a al eje de abscisas
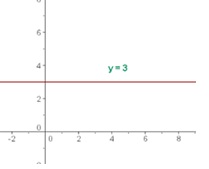
3. FUNCIONES POLINÓMICAS DE PRIMER GRADO
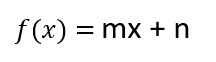
Su gráfica es una recta oblicua, que queda definida por dos puntos de la función.
Son funciones de este tipo las siguientes:
- Función afín: f(x) = mx
- Función lineal: f(x) = x
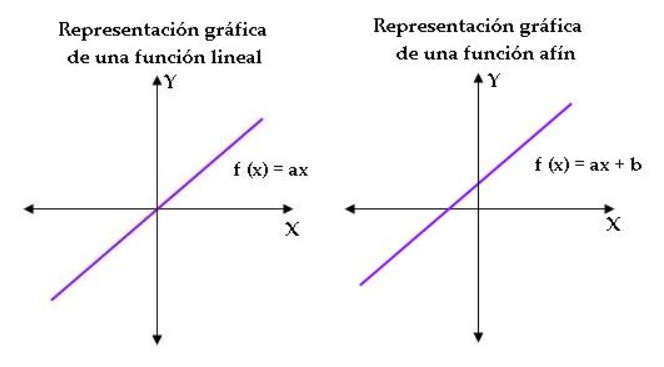
4. FUNCIONES RACIONALES
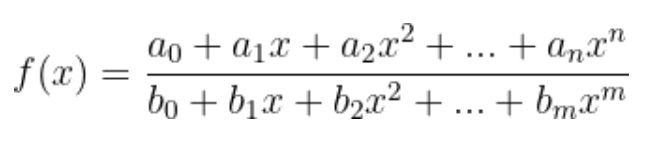
Las funciones racionales pueden tener características que las diferencian de las funciones polinómicas y que vamos a revisar:
- Singularidades: En algunos casos, algunos valores de x son problemáticos. Esto es debido a que las funciones racionales hay un denominador que puede ser 0 y no podemos dividir entre 0. Esos valores de x que hacen 0 el denominador juegan un papel especial. Como no podemos calcular el valor de la función en esos valores decimos que la función no está definida para esos valores de x.
También decimos que esos puntos no pertenecen al dominio de la función. El dominio de una función racional está determinado por las restricciones impuestas por el denominador: dividir entre 0 es imposible.
El dominio es el conjunto de los números reales para los que la función está definida. En el caso de las funciones racionales es el conjunto de todos los números reales que no son ceros del denominador. Por lo tanto, para determinar el dominio de una función racional tenemos que encontrar los ceros reales del denominador.
A estos puntos se les llama singularidades y es interesante ver cómo se comporta la función cerca de esos puntos.
- Continuidad: Las funciones racionales son continuas en su dominio (pero su dominio puede no ser todos los números reales).
- Comportamiento "en el infinito": Es interesante el estudio del comportamiento de la función cuando x se hace más y más grande en valor absoluto (siendo x positivo o negativo). Veremos que en algunos casos la función se aproxima a una recta (horizontal u oblicua). En estos casos diremos que la función tiene una asíntota horizontal u oblicua (según los casos). En todos los casos el comportamiento de una función racional "en el infinito" está determinado por una función polinómica.
Ejemplo1:
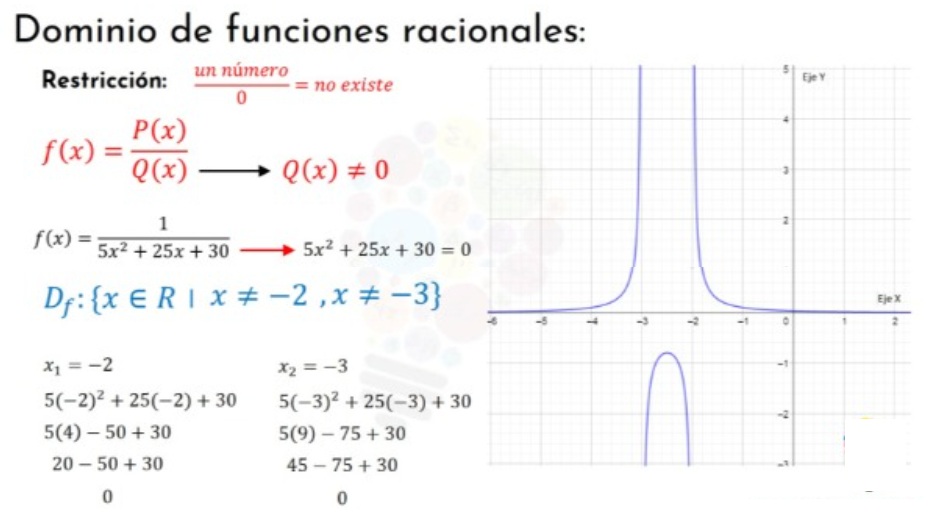
Ejemplo2:
Hallar el dominio, rango, punto de corte con el eje X y con el eje Y de la función y sus asíntotas:
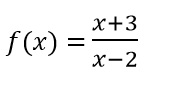
Primero hallamos las singularidades:
Dominio = X - 2 ≠ 0
X ≠ 2
Df : X Ɛ R - {2}
Segundo, verificamos los valores de proximidad tanto por la izquierda como por la derecha a 2
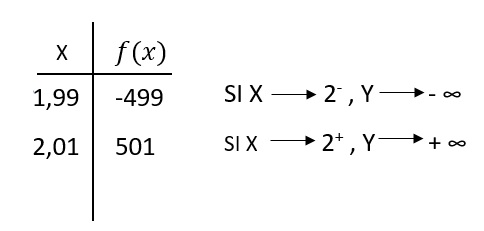
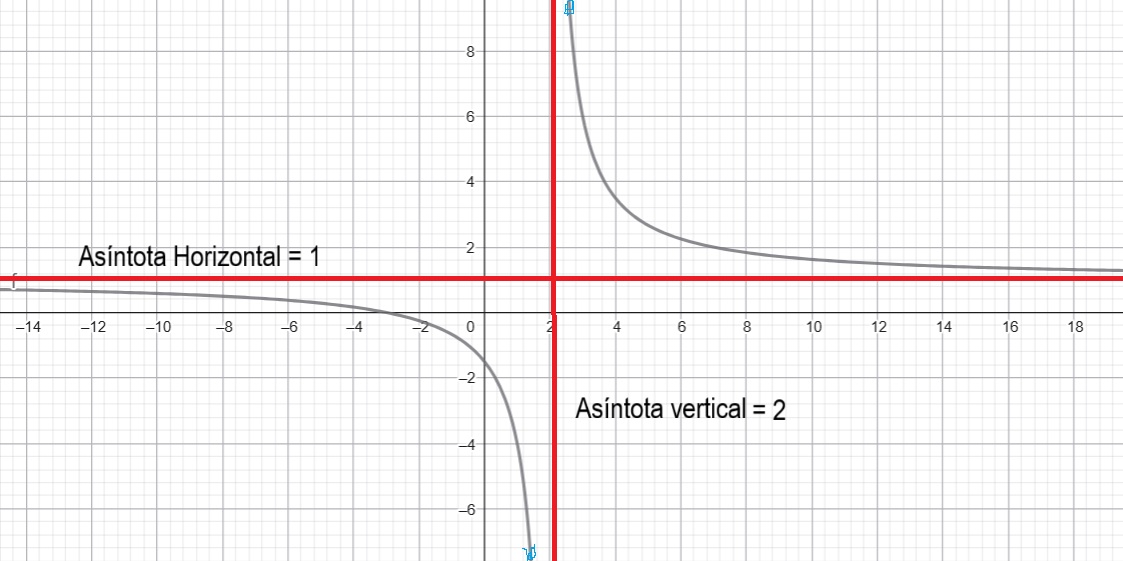
Para hallar los cortes con el eje X hacemos Y o f(x) = 0, pero esto recuerda que el numerador hace referencia al eje Y,
X + 3 = 0; X = -3
Para hallar los cortes con el eje y hacemos X = 0, es decir:
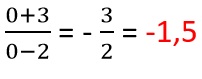
X - 2 = 0; X = 2
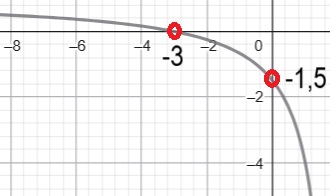
En este punto ya podemos hallar el rango, es decir los valores de Y:
Rf : y Ɛ R - {1}
5. FUNCIONES RADICALES
El criterio viene dado por la variable x bajo el signo radical.
El dominio de una función irracional de índice impar es R.
Ejemplo:
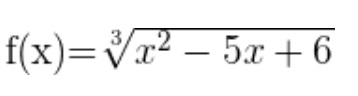
El dominio de una función irracional de índice par está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
Ejemplo 1:
Hallar dominio y rango de la función:
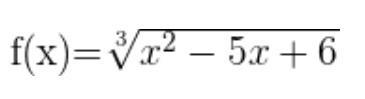
Como el índice radical de f(x) es impar, entonces el dominio de f(x) son todos los números reales .
Rf=X Ɛ R <= -0,63
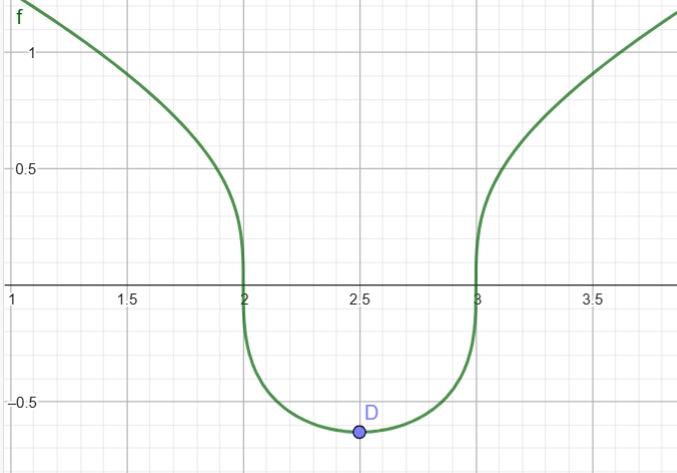
Ejemplo 2: Radical racional
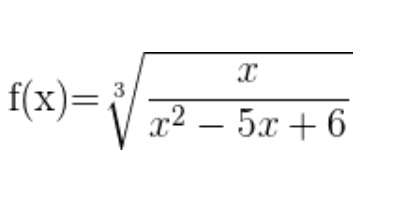
Como el índice radical de f(x) es impar, entonces el dominio de f(x) debería ser todos los números reales R, pero al mismo tiempo posee un denominador que se hace cero cuando x = 2 y 3 . Entonces:
Df = X Ɛ R - {2,3}
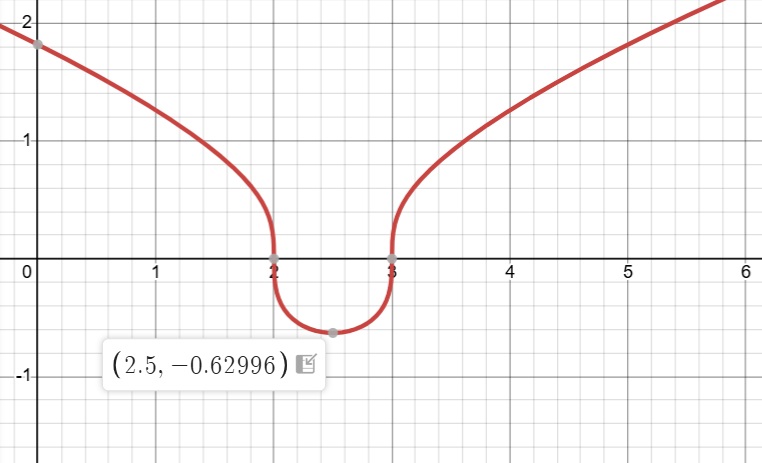
Gráfica de la función cuadrática del denominador
Combinando ambas informaciones del radical su gráfica es la siguiente:
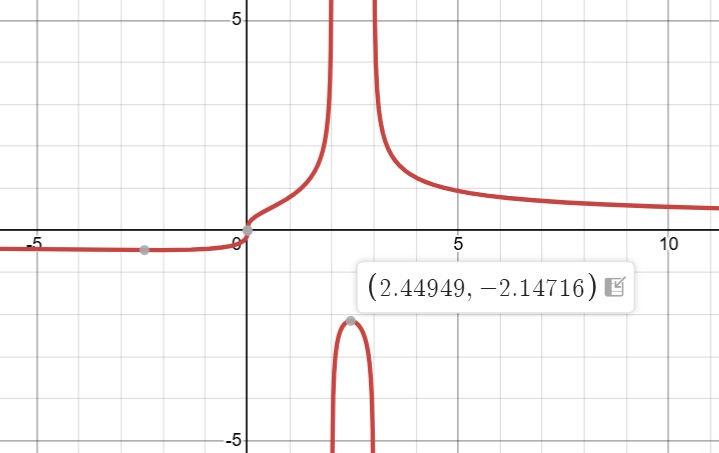
Df = X Ɛ R - {2,3}
Rf = X Ɛ R - {-0,4645=>x>=-2,14716}
Ejemplo3: Función radical de índice par
El dominio está formado por todos los valores que hacen que el radicando sea mayor o igual que cero.
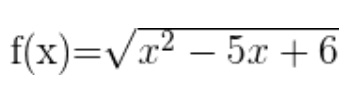
Para calcular el dominio hacemos el radicando mayor o igual que cero
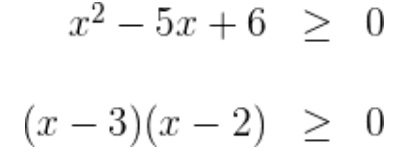
Los valores x=(2,3) dividen la recta real en tres intervalos:
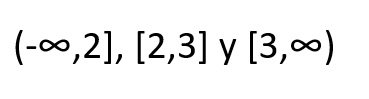
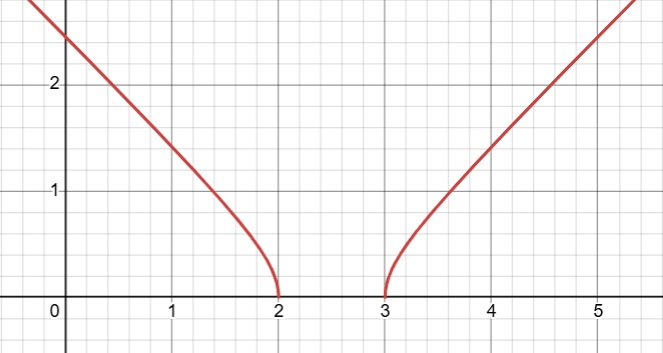
Verificamos cuales de los tres intervalos satisfacen la desigualdad, los que satisfagan conformarán el dominio, quedando:
Df(x) = (-∞, 2] U [3 ,∞)
Para entender mejor el tema, te invito a observar el siguiente video:
6. FUNCIONES ALGEBRAICAS DEFINIDAS A TROZOS
Son funciones definidas por distintos criterios, según los intervalos que se consideren.
Ejemplo1:
Para las siguientes funciones, dibuja su gráfica y determina su dominio y rango.
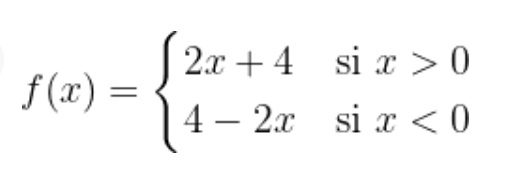
Solución:
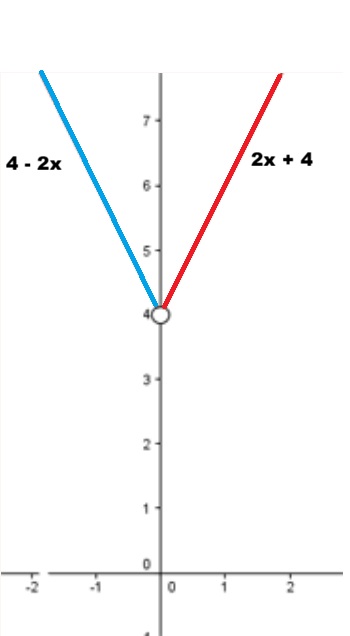
Notemos que en el intervalo (0,∞) es decir, - del lado derecho del plano— tenemos la función 2x + 4
Por otro lado, en el intervalo (-∞ , 0) —lado izquierdo del plano—, tenemos la función 4 - 2x
Por tanto, la gráfica es como se muestra en la siguiente figura:
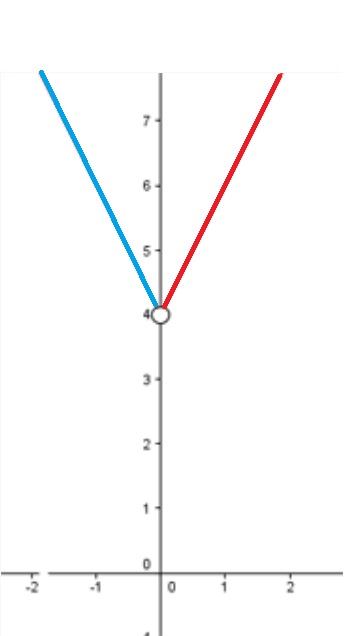
Como mencionamos anteriormente, la función está definida para (0,∞) y para (-∞ , 0). Por lo tanto, el dominio es:
Df(x) = (0,∞) U (-∞ , 0) = R - 0
Por otro lado, de la gráfica podemos ver que el rango es
Rf(x) = (4 , ∞)
Ejemplo 2:
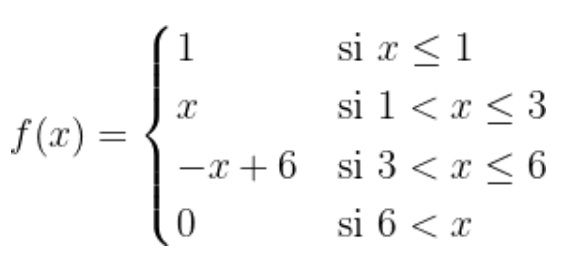
Solución:
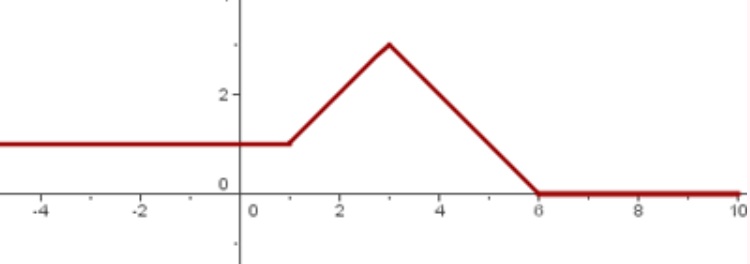
Notemos que la función está definida para cuatro regiones distintas. Primero, para el intervalo
(-∞ , 1) tiene el valor 1. Luego, para el intervalo (1,3) tiene el valor de x y así sucesivamente.
Luego, notemos que el dominio es:
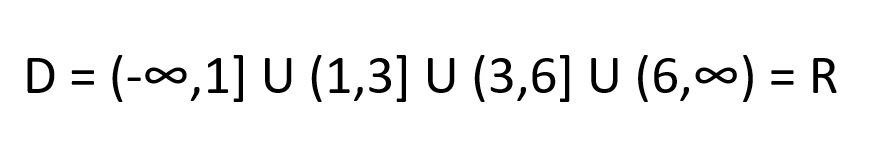
Por otro lado, notemos que el rango es:
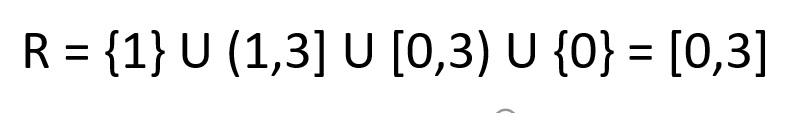
ACTIVIDAD 4.
1. Cual es el dominio de la siguiente funión polinomial?
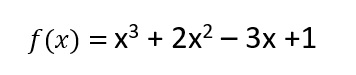
2. Hallar el dominio, rango, punto de corte con el eje X y con el eje Y de la función y sus asíntotas de la función:
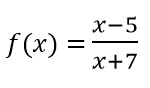
3. Encontrar las siguientes palabras en la sopa de letras:

4. Calcular el dominio y rango y diseñar su gráfica:
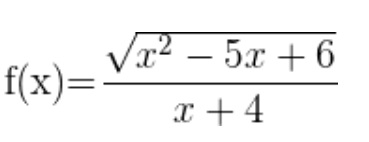
5. Hallar la función definida a trazos:
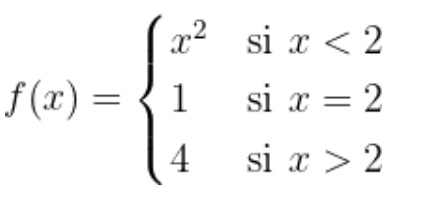
FUNCIONES TRASCENDENTES
1. FUNCIONES EXPONENCIALES
Son aquellas que tienen la forma:
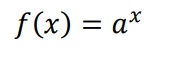
Siendo a un número real distinto de 1
Casos:
- Primer Caso: a > 1 (base mayor a 1)
Ejemplo 1. Bosqueje el grafico de la función:
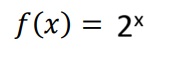
Recomendación: siempre realizar la tabla con 5 valores
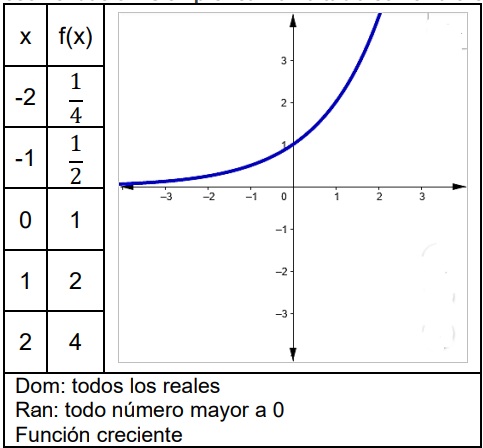
- Segundo Caso: 0 < a < 1 (base, número racional entre 0 y 1)
Ejemplo 2. Bosqueje el gráfico de la función :
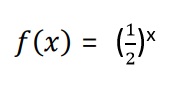
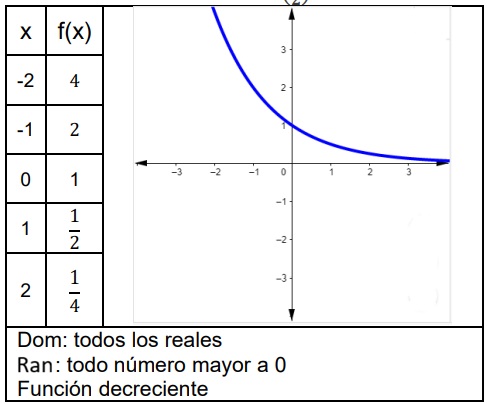
Actividad 5:
Realiza el bosquejo de las siguientes funciones
1. FUNCIONES LOGARÍTMICA
Se define logaritmo como el exponente de una potencia con cierta base, es decir, el número al cual se debe elevar una base dada para obtener un resultado determinado.

Gráfica de una función logarítmica:
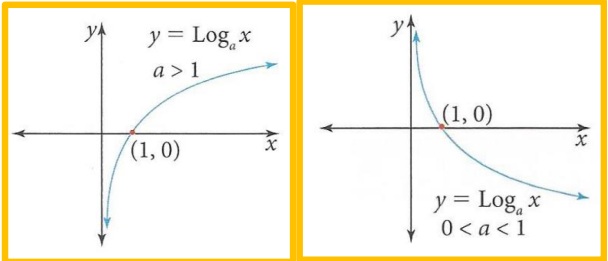
Te invito a realizar el anterior ejercicio en geogebra.
REPRESENTACION GRAFICA DE LA FUNCION LOGARITMICA
Para representar grafica la función logarítmica 𝑦 = log𝑎 𝑥 se realiza lo siguiente:
1. Se determinan los principales puntos cuando x=1 y cuando x=a
2. Se construye una tabla de valores
3. Se ubican los puntos en el plano cartesiano y se unen mediante una línea curva
Cuando a>1 se tiene que:
- La función 𝑦 = log𝑎 𝑥 es creciente
- Cuando el valor de x disminuye 𝑓(𝑥) tiende a −∞
- Cuando el valor de a disminuye la gráfica de la función crece más rápidamente
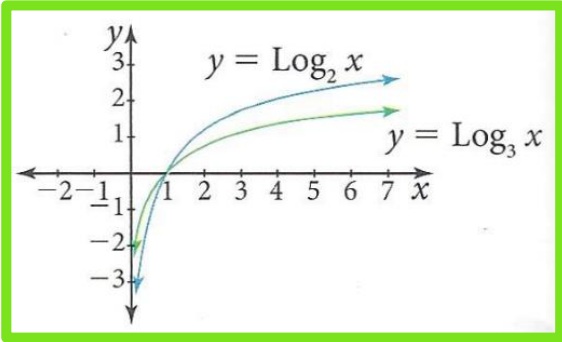
Cuando 0<a<1 se tiene que
- La función 𝑦 = log𝑎 𝑥 es decreciente
- Cuando el valor de x disminuye 𝑓(𝑥) tiende a ∞
- Cuando el valor de a aumenta, la gráfica de la función decrece más rápidamente
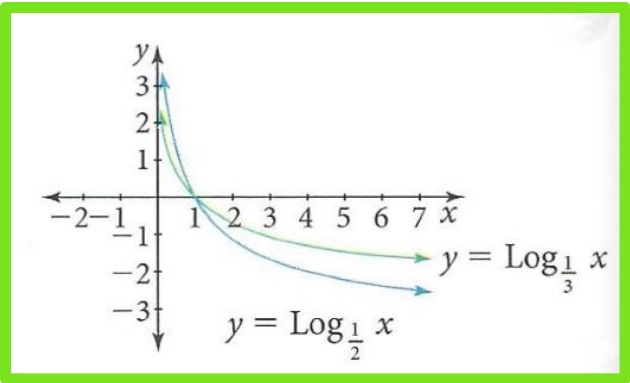
Ejemplo1
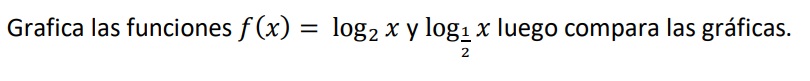
1. Primero se construye la tabla de valores teniendo en cuenta que 𝑥 ∈ ℝ+
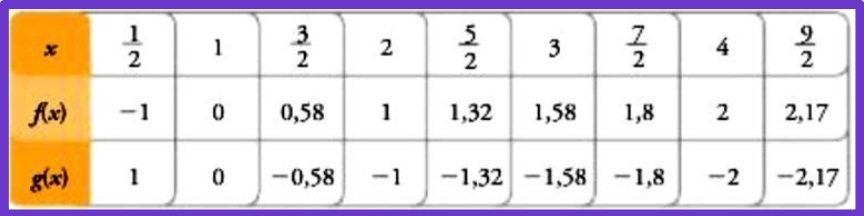
2. Luego se ubican los puntos en el plano cartesiano y se unen mediante una curva. Es importante tener en cuenta que para mayor facilidad en la gráfica se puede utilizar papel milimetrado y utilizar curvígrafo.
3. Al realizar las gráficas en un solo plano cartesiano quedaran de la siguiente forma.
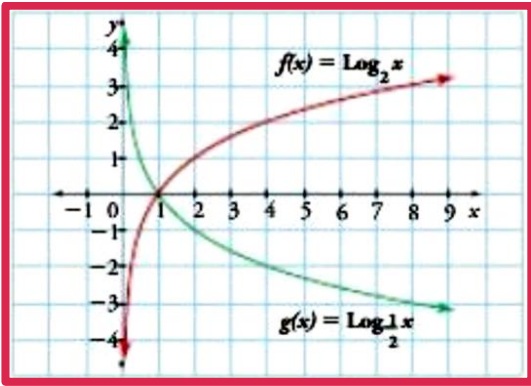
Ejemplo2
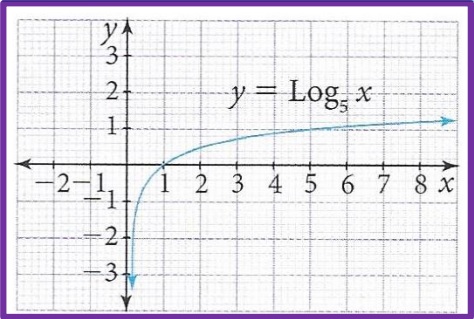
Trace la gráfica de la función 𝑦 = log5 𝑥
1. Primero se determinan los puntos cuando 𝑥 = 1 y 𝑥 = 5
𝑓(1) = log5 1 = 0
𝑓(5) = log5 5 = 1
Por tanto, la gráfica pasa por los puntos (1,0) y (5,1)
2. Luego se construye la tabla de valores teniendo en cuenta que 𝑥 ∈ ℝ+
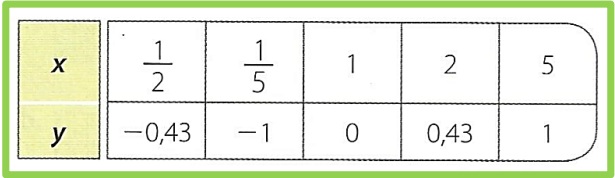
3. Finalmente se ubican los puntos en el plano cartesiano y se unen mediante una línea curva
Ejemplo3
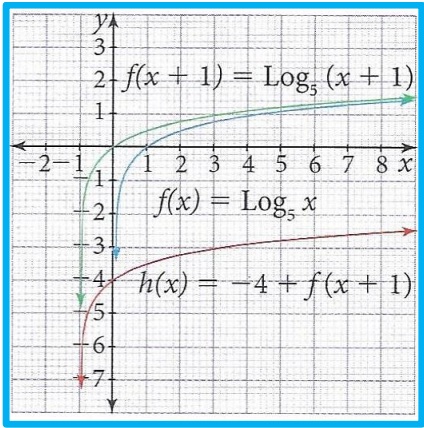
Trace la gráfica de la función ℎ(𝑥) = −4 + log5
(𝑥 + 1); utilizando las propiedades de las funciones .
La función principal es log5 𝑥 por tanto vamos a partir de esta función, como en la función ℎ(𝑥) aparece
log5
(𝑥 + 1) quiere decir que la función se debe trasladar una unidad hacia la izquierda, además se le resta
4, esto quiere decir que se traslada 4 unidades hacia abajo para así obtener la gráfica de ℎ(𝑥)
Para el siguiente ejercicio te invito a observar el siguiente video sobre la difetencia entre logaritmo y logaritmo natural.
Ejemplo4
Halle el dominio y el rango de 𝑔(𝑥) = 4 + 𝐿𝑛(2𝑥 − 3)
El dominio de toda función logarítmica comprende solo valores positivos por tanto el argumento del logaritmo debe ser mayor a cero, entonces tenemos 2𝑥 − 3 > 0 Para hallar los valores de x que definen la función se debe solucionar la desigualdad 2𝑥 − 3 > 0
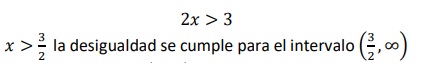
por tanto, el dominio de la función es 𝔻 = (3/2, ∞)
Y el rango de una función logarítmica son todos los números Reales
Si no te quedó claro el tema, te invito a observar el siguiente video:
Actividad 6
1. Relaciona cada una de las siguientes funciones logarítmicas con la gráfica correspondientes:
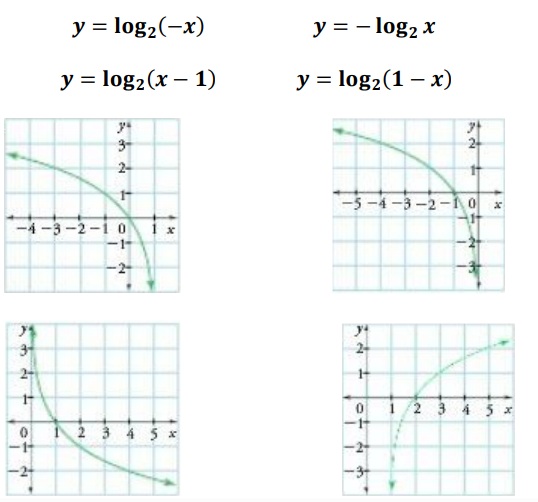
2. Completa la siguiente tabla:

3. En un laboratorio un cultivo de bacterias crece según la función:
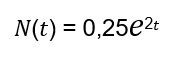
donde t es el tiempo en horas y 𝑒 ≈ 2,7182.
a. Exprese el tiempo en función del número de bacterias
b. Calcula el tiempo necesario para que haya aproximadamente 2025 bacterias.
FUNCIONES TRIGONOMÉTRICAS
Todas las funciones trigonométricas son básicamente las proporciones trigonométricas de cualquier ángulo dado. Por ejemplo, si es que tomamos a las funciones f(x)=sin(x), f(x)=tan(x), etc., estamos considerando a estas proporciones trigonométricas como funciones. El dominio y el rango de estas funciones trigonométricas dependerá en la naturaleza de sus proporciones trigonométricas correspondientes.
A continuación, conoceremos el dominio y el rango de las funciones trigonométricas fundamentales como seno, coseno y tangente. También, veremos el dominio y el radio de las funciones cosecante, secante y tangente.
Dominio y rango de funciones trigonométricas (sin, cos, tan)
SENO
Podemos empezar considerando a la identidad trigonométrica más simple:
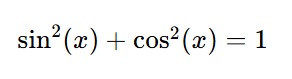
De esta identidad, podemos derivar las siguientes interpretaciones:
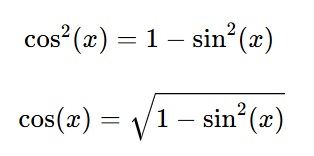
Sabemos que la función coseno está definida para valores reales, por lo que el valor dentro de la raíz cuadrada no puede ser negativo. Entonces, podemos formar la desigualdad:
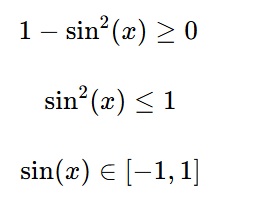
Entonces, ya hemos obtenido el dominio y el rango para la función seno. El dominio es todos los números reales de x ya que no tenemos ninguna restricción en los valores de x. El rango es desde -1 hasta 1, incluyendo a estos valores. Podemos comprobar esto mirando su gráfica:
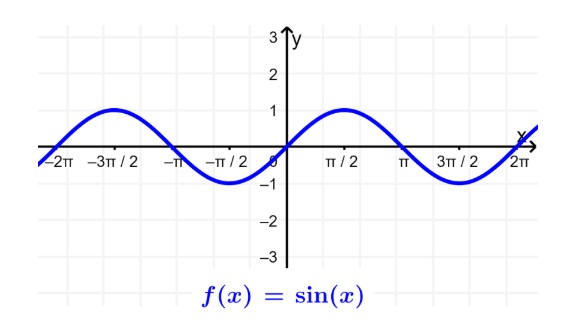
COSENO
De igual forma, usando la misma metodología, tenemos:
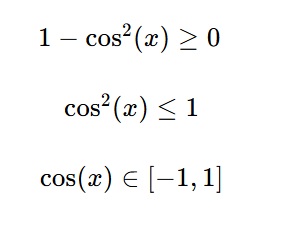
Entonces, el dominio de la función coseno también es todos los números reales de x. El rango de la función coseno es desde -1 hasta 1, incluyendo a estos valores. Podemos verificar esto mirando su gráfica:
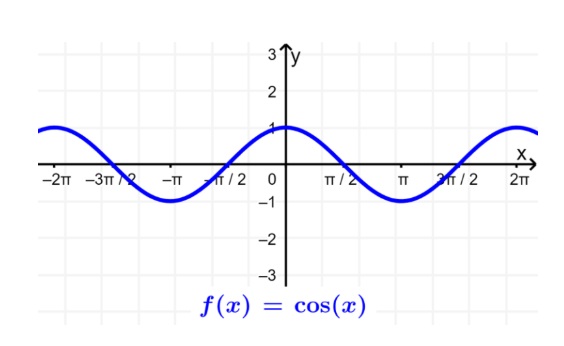
Algo importante que debemos tener en cuenta es que el rango de seno y coseno depende de la amplitud de las funciones. Por ejemplo, si tenemos f(x)=5cos(x), el rango es desde -5 a 5.
TANGENTE
Ahora, miremos la función f(x)=tan(x). Sabemos que tan(x)=sin(x)/cos(x). Esto significa que la función tangente está definida para todos los valores a excepción de aquellos que hacen que cos(x) sea igual a cero, ya que una fracción con denominador igual a cero es indefinida.
Ahora, sabemos que cos(x) es cero para los ángulos:
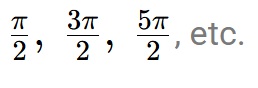
Por lo tanto, el dominio de la función tangente es:
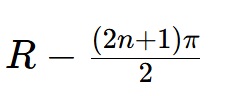
y el rango es todos los números reales. Podemos ver esto en la gráfica:
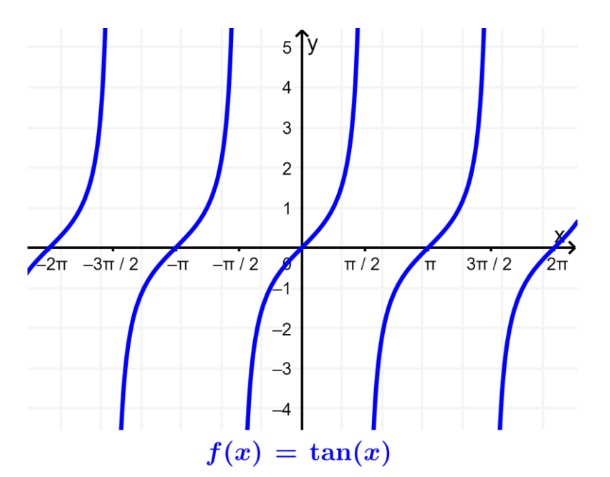
Dominio y rango de las funciones cosec, sec y cot
SECANTE
Sabemos que la secante es la función recíproca del coseno. Entonces, tenemos:
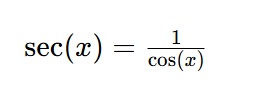
Eso significa que la secante no estará definida para los puntos en donde cos(x)=0. Entonces, el dominio de f(x)=sec(x) será:
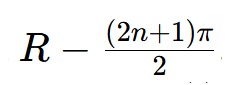
El rango de la secante será R−(−1,1). Dado que cos(x) se ubica entre -1 hasta 1, la secante nunca puede estar en esta región. Podemos mirar su gráfica:
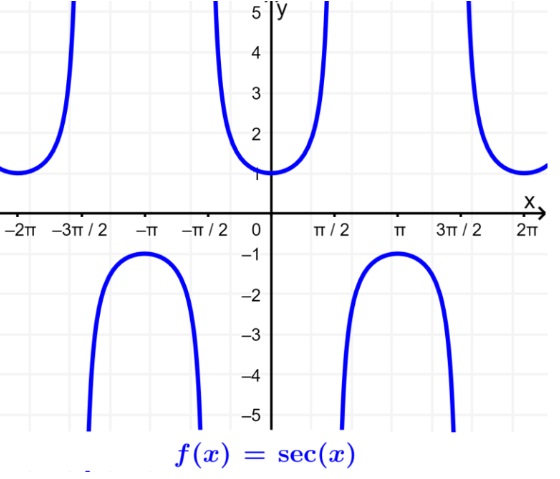
COSECANTE:
La cosecante es la función recíproca del seno. Entonces, tenemos:
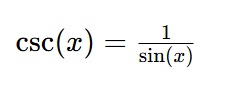
Sabemos que la cosecante no estará definida para los puntos en donde sin(x)=0. Por lo tanto, el dominio de f(x)=csc(x) será R−nπ.
El rango de la cosecante será R−(−1,1). Esto se debe a que sin(x) se ubica entre -1 hasta 1, por lo que la cosecante nunca puede estar en esta región. Podemos comprobarlo con su gráfica:
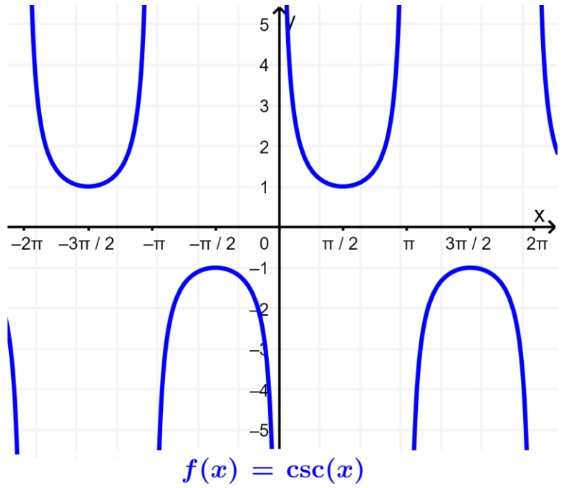
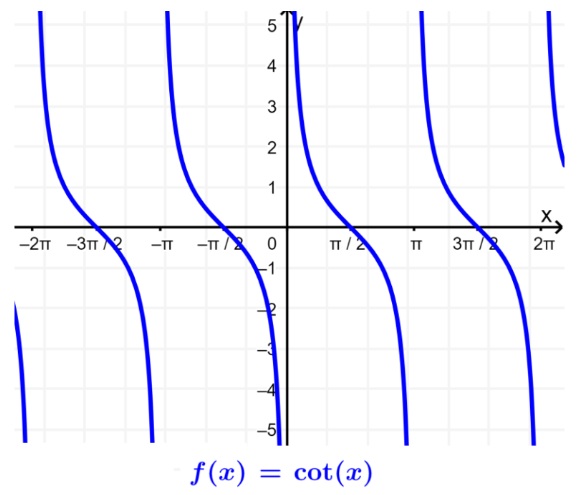
COTANGENTE
La cotangente es la función recíproca de la tangente. Entonces, tenemos:
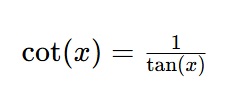
La función cotangente no estará definida para los puntos en donde tan(x)=0. Entonces, el dominio de f(x)=cot(x) será R−nπ.
El rango de la cotangente será R−(−1,1) el conjunto de todos los números reales porque no tenemos ninguna restricción. Podemos mirar su gráfica:
Actividad 7
Calcular el dominio de las funciones trigonométricas
1. f(x)=sen(5x+8)
2. f(x)=cos(8x-4)
3. f(x)=tan(x+1)
4. f(x)=sec(3x2+2)
5. f(x)=cot(3x2+2)
5. OPERACIONES ENTRE FUNCIONES

Actividad 8:
En los siguientes ejercicios se definen las funciones f y g Determine las funciones resultantes
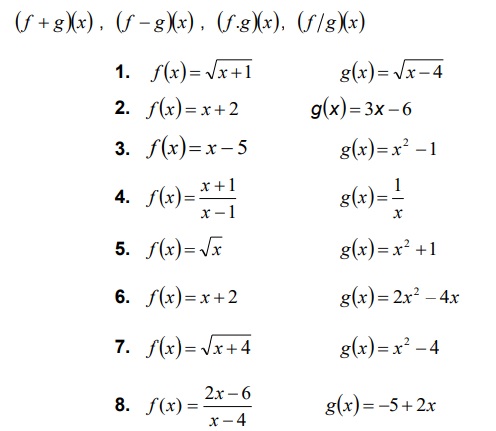
HETEROEVALUACIÓN
La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
GUÍA DE APRENDIZAJE
En caso de no poseer internet, descarga aquí la guía de aprendizaje.
ACUERDOS PEDAGÓGICOS
RÚBRICA
1. Rúbrica rángo y función:
2. Rúbrica propiedades de las funciones: