GRADO 10
TRIGONOMETRÍA - SEGUNDO PERIODO
DBA 4. Comprende y utiliza funciones para modelar fenómenos periódicos y justifica las soluciones.
Estándar Básico de Competencia: Analizo en representaciones gráficas cartesianas los comportamientos de cambio de funciones específicas pertenecientes a familias de funciones polinómicas, racionales, exponenciales y logarítmicas.
CONOCIMIENTOS PREVIOS


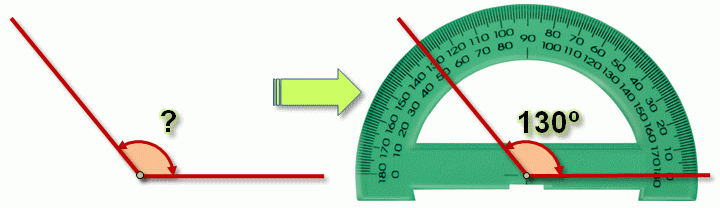
Medida de ángulos con el transportador
El proceso es muy sencillo:
- Colocamos el transportador de manera que el vértice del ángulo coincida con el centro del transportador.
- Hacemos que uno de los lados pase por el punto de 0º del transportador.
- Miramos y anotamos la medida por donde pasa el otro lado. Esta medida se expresa en grados.
Si es necesario prolongamos los lados del ángulo para poder medirlos.
Observa el siguiente video:
EJERCICIOS
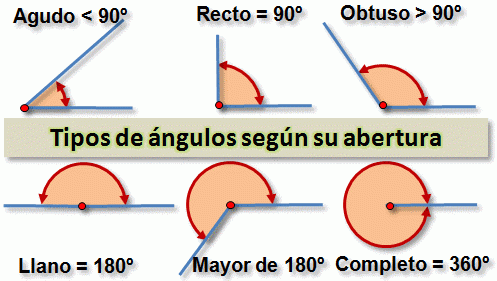
1. Con mis compañeros repaso oralmente las características de los siguientes ángulos. Con toda la información recolectada organizo las definiciones y las consigno en el cuaderno:
a. Agudo b. Recto
c. Obtuso d. Complementario
e. Suplementario f. Llano
g. De una vuelta
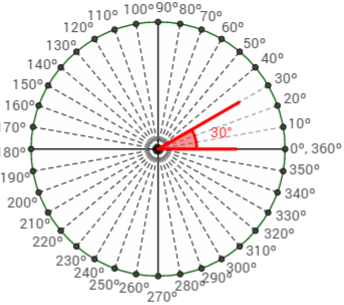
2. En mi cuaderno dibujo los ángulos dados, para facilitar el proceso, ordeno los ángulos de menos a mayor:
a. 53° b. 225° c. 270°
d. 135° e. 300° f. 90°
g. 180° h. 350° i. 25°
3. En mi cuaderno realizo los siguiente ejercicios, puedo comparar mis respuestas con la de mis compañeros:
a. Dibujo 2 ángulos complementarios, escribo las medidas de cada uno.
b. Dibujo 2 ángulos suplementarios, tal que uno de ellos mida 120°
c. Si un ángulo mide 15°, 21° y 40° cuanto mide su complemento?
d. Si un ángulo mide 140°, 17°, 51° cuanto mide su suplementario?
1. ÁNGULOS
1.1. Sistema sexadecimal.
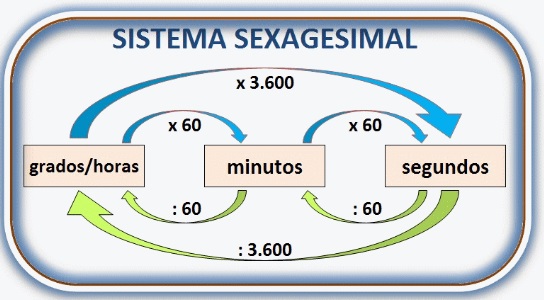
Este sistema lo usamos para medir tiempos (horas, minutos y segundos), ángulos (grados, minutos y segundos) y coordenadas cartesianas para situar una posición.
El sistema sexagesimal es un sistema de numeración posicional que emplea como base el número 60.
El grado sexagesimal, como unidad del sistema de medida de ángulos sexagesimal, está
definido partiendo de que un ángulo recto tiene 90° (90 grados sexagesimales), y sus
divisores, el minuto sexagesimal y el segundo sexagesimal, están definidos del siguiente
modo:
1. ángulo recto = 90° (grados sexagesimales).
2. 1 grado sexagesimal = 60′ (minutos sexagesimales). También 1 Hora = 60'
3. 1 minuto sexagesimal = 60″ (segundos sexagesimales).
Esta notación sexagesimal tiene su origen en Mesopotamia, donde los astrónomos y
matemáticos usaron para sus cálculos frecuentemente números en sistema sexagesimal, lo
cual facilitaba sus cálculos.
Observa en el cuadro siguiente que la abreviatura para minutos y segundos es diferente en ángulos y en la medida del tiempo aunque se denominan igual. Por lo demás tanto las medidas y operaciones con las unidades de ángulos y del tiempo se realizan de la misma manera:
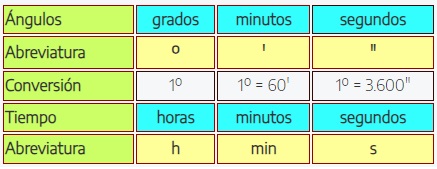
1.1.1. Notación sexadecimal
Podemos expresar una cantidad en grados, minutos y segundos; las partes de grado inferiores al segundo se expresan como parte decimal de segundo.

Ejemplos:
1. 25°34′39″ se lee 25 grados, 34 minutos y 39 segundos.
2. 73°3′23,8″ se lee 73 grados, 3 minutos y 23,8 segundos.
3. 124°45′34,70″
4. -2°34′10″
Nota: Por norma de notación, no se debe dejar espacio entre las cifras
1.1.2. Operación con Ángulos
SUMA DE ANGULOS:
1. Para sumar grados expresados en medidas complejas, primero se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos, y se suman
2. Si al sumar los segundos el resultado es mayor que 60 se divide entre 60, el cociente se añade a los minutos y el resto queda como segundos.
3. Se hace lo mismo con los minutos.
Veamos el siguiente ejemplo:

Ejercicio:
1. Efectúa las siguientes operaciones en tu cuaderno:
a) 15° 22' 30" + 8° 27' 41" b) 50' 43" + 13' 10" c) 1° 44' 11" + 5° 16' 9"
d) 2° 7' + 17° 49' 54" e) 320° 32" 22'' + 23' 2" e) 12° 14' 15" + 55° 26' 18"
RESTA DE ANGULOS:
Para restar se procede igual.
Se escriben las medidas de manera que coincidan en columnas las unidades del mismo orden y se restan.
Si al restar los segundos es menor el minuendo, convertimos un minuto del minuendo en segundos y sumamos 60" al orden de los segundos.
- Se hace lo mismo con los minutos.
Veamos el siguiente ejemplo: 28º 32' 23" - 13º 54' 24" = 14º 37' 59"

Nota: 23" es menor que 24" por tanto, le quitamos 1' a la columna de los minutos (32') y se lo agregamos a los segundos, es decir, 23"+60"=83"
Observa la siguiente página donde restaremos ángulos:
https://edu.gcfglobal.org/es/geometria-basica/resta-de-angulos/1/
Práctica:
Antes de realizar ejercicios en el cuaderno ingresa datos de una resta y observa los resultados en la siguiente página:
Ejercicio:
1. Efectúa las siguientes operaciones en tu cuaderno:
a) 4° 11' 17" − 1° 16' 32" b) 50' 43" − 3' 50" c) 11° 44' 11" − 5° 16' 39"
d) d) 12° 7' 55" − 7° 49' 54" e)
MULTIPLICACIÓN DE ANGULO POR UN NÚMERO:
Para multiplicar un ángulo por un número natural se realizan los siguientes pasos:
Ejemplo: Mulitplicar 27°18"34' Por 4
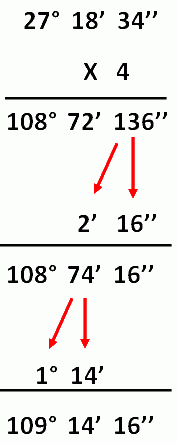
1) Se multiplican los grados, minutos y segundos por el número (4)
2) Si los segundos sobrepasan los 60, se pasan a minutos (136'' = 2' 16'') y los minutos formados se suman con los minutos (72' + 2' = 74').
3) Si los minutos resultantes sobrepasan los 60, se pasan a grados (74' = 1° 14') y los grados formados se suman con los grados (108° + 1° = 109°).
Ejercicio:
Para verificar que entendiste el procedimiento te invito a contestar el ejercicio que se encuentra en el siguiente link:
https://www.ceiploreto.es/sugerencias/ceibal/Operaciones_con_angulos/ejercicio.html
DIVISIÓN DE ANGULO POR UN NÚMERO:

Dividir 37º 48' 25'' entre 5
1er paso:
Se dividen las horas (o grados) entre el número.
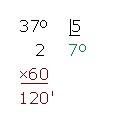
2o paso:
El cociente son los grados y el resto, multiplicando por 60, los minutos.
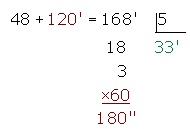
3er paso:
Se añaden estos minutos a los que tenemos y se repite el mismo proceso con los minutos.
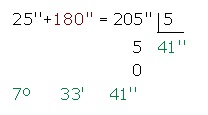
4o paso
Se añaden estos segundos a los que tenemos y se dividen los segundos.
Otras unidades de tiempo que no forman un sistema sexagesimal:
- 1 día = 24 horas.
- 1 semana = 7 días.
- 1 mes = 28, 29, 30 o 31 días.
- 1 trimestre = 3 meses.
- 1 cuatrimestre = 4 meses.
- 1 semestre = 6 meses.
- 1 año = 365 días (366 si es bisiesto).
- 1 lustro o quinquenio = 5 años.
- 1 década = 10 años.
- 1 siglo = 100 años.
- 1 milenio = 1.000 años.
RELACIÓN ENTRE ÁNGULOS
Entre 2 ángulos se pueden establecer distintas relaciones:
Ángulos consecutivos: Son aquellos que tienen en común el vértice y uno de los lados.
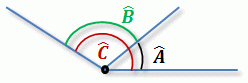
Los ángulos A y B son consecutivos y juntos suman lo mismo que el ángulo C.
Hay dos casos especiales de ángulos consecutivos, según el ángulo que suman entre ambos:
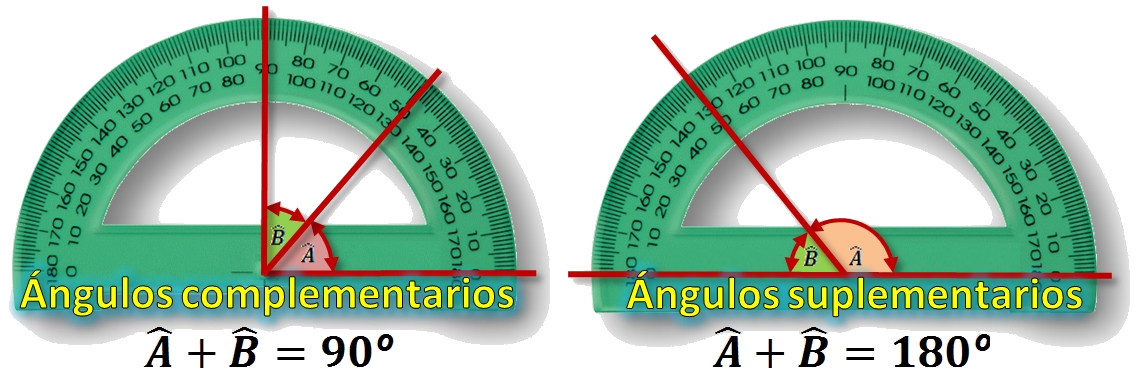
Son dos ángulos consecutivos que suman 90 grados, formando su unión un ángulo recto.
La suma de estos dos ángulos forman un ángulo recto (50º + 40º = 90º).
Ángulos suplementariosSon dos ángulos consecutivos que suman 180 grados, formando su unión un ángulo llano.
La suma de estos dos ángulos forman un ángulo llano (130º + 50º = 180º).
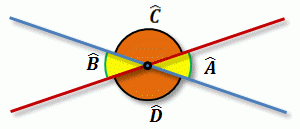
Ángulos opuestos por el vértice: cada lado de un ángulo es prolongación del lado del otro ángulo. Se forman 4 ángulos opuestos que son iguales dos a dos.