Grado 10

ESTADÍSTICA - PERIODO 2

DBA 9. Comprende y explica el carácter relativo de las medidas de tendencias central y de dispersión, junto con algunas de sus propiedades y la necesidad de complementar una medida con otra para obtener mejores lecturas de los datos.

Estándar básico de competencia: Resuelvo y planteo problemas usando conceptos básicos de conteo y probabilidad (combinaciones, permutaciones, espacio muestral, muestreo aleatorio, muestreo con reemplazo).

1. MEDIDAS DE TENDENCIA CENTRAL

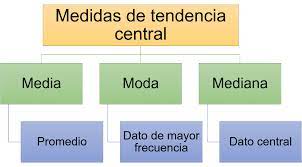
Las medidas de tendencia central son funciones estadísticas que pretenden resumir en un solo valor a un conjunto de valores. Representan un centro en torno al cual se encuentra ubicado el conjunto de los datos.

Las medidas de tendencia central (media, mediana y moda) sirven como puntos de referencia para interpretar las calificaciones que se obtienen en una prueba.

En resumen, el propósito de las medidas de tendencia central es:

Mostrar en qué lugar se ubica la persona promedio o típica del grupo.
Sirve como un método para comparar o interpretar cualquier puntaje en relación con el puntaje central o típico.
Sirve como un método para comparar el puntaje obtenido por una misma persona en dos diferentes ocasiones.
Sirve como un método para comparar los resultados medios obtenidos por dos o más grupos.

Las medidas de tendencia central más comunes son: La media aritmética: comúnmente conocida como media o promedio. Se representa por medio de una letra X con una línea en la parte superior.

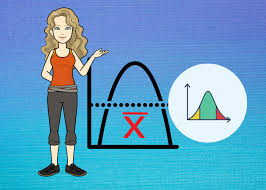
Podemos decir que la fórmula general para estos datos que son no agrupados es:

1.1. Média aritmética

También llamada promedio o simplemente media, se obtiene con la suma de un conjunto de valores dividida entre el número total de sumandos.

Ejemplo: En matemáticas, un alumno tiene las siguientes notas: 4, 7, 7, 2, 5, 3

n = 6 (número total de datos)

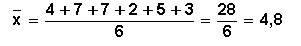
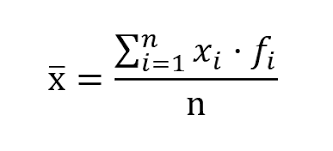
Ejercicio1.

El profesor de la materia de estadística desea conocer el promedio de las notas finales de los 10 alumnos de su clase. Las notas de los alumnos son:

3,2; 3,1; 2,4; 4,0; 3,5; 3,0; 3,5; 3,8; 4,2; 4,0

1.2. Mediana (Me)

La mediana: Es el puntaje que se ubica en el centro de una distribución. Se representa como Md.

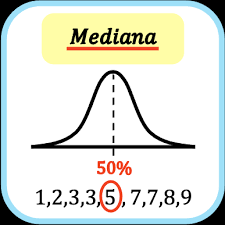
La mediana representa el valor de la variable de posición central en un conjunto de datos ordenados. Si la serie tiene un número par de puntuaciones, la mediana es la media entre las dos puntuaciones centrales

La Mediana no tiene propiedades que le permite intervenir en desarrollos algebraicos como la media aritmética, sin embargo, posee propiedades que ponen en evidencia ciertas cualidades de un conjunto de datos, lo cual no ocurre con la media aritmética que promedia todos los valores y suprime sus individualidades. En cambio, la mediana destaca los valores individuales.

Tiene la ventaja de no estar afectada por las observaciones extremas, ya que no depende de los valores que toma la variable, sino del orden de las mismas

Para el cálculo de la mediana interesa que los valores estén ordenados de menor a mayor.

Su aplicación se ve limitada, ya que solo considera el orden jerárquico de los datos y no alguna propiedad propia de los datos, como en el caso de la media aritmética.

Para reconocer la mediana, es necesario tener ordenados los valores sea de mayor a menor o lo contrario. Usted divide el total de casos (N) entre dos, y el valor resultante corresponde al número del caso que representa la mediana de la distribución.

Según el número de valores que se tengan se pueden presentar dos casos:

Si el número de valores es impar, la Mediana corresponderá al valor central de dicho conjunto de datos.

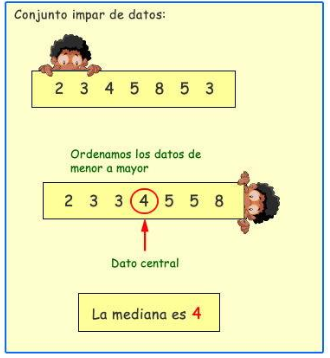
Si el número de valores es par, la Mediana corresponderá al promedio de los dos valores centrales (los valores centrales se suman y se dividen por 2).

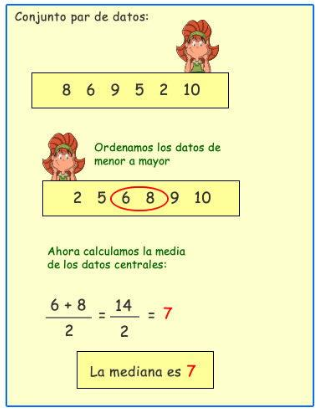
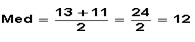
Ejemplo: Se tienen los siguientes datos: 5, 4, 8, 10, 9, 1, 2

Al ordenarlos en forma creciente, es decir de menor a mayor, se tiene: 1, 2, 4, 5, 8, 9, 10 El 5 corresponde a la Med, porque es el valor central en este conjunto de datos impares.

Ejemplo 2: El siguiente conjunto de datos está ordenado en forma decreciente, de mayor a menor, y corresponde a un conjunto de valores pares, por lo tanto, la Med será el promedio de los valores centrales.

21, 19, 18, 15, 13, 11, 10, 9, 5, 3

Para afianzar más tu conocimiento te invito a observar el siguiente video:

Ejercicio 2.

Los jugadores de 2 equipos se pesaron. Los datos de masa corporal se muestran a continuación:
Equipo A: 72,65,66,56,59,63,61,70.
Equipo B: 61,82,76,73,77,70,69,68.

Calcular la mediana de cada equipo.

1.3. Moda (Mo)

La moda de un conjunto de datos es simplemente el número que más se repite o que tiene mayor frecuencia absoluta.

Un conjunto de datos puede no tener moda o tener más de una moda.

Ejemplo:

Una empresa de transporte terrestre selecciona los sitios de Boyacá con mayor demanda de pasajes. Para cada uno registró el número de pasajes vendidos durante una semana.

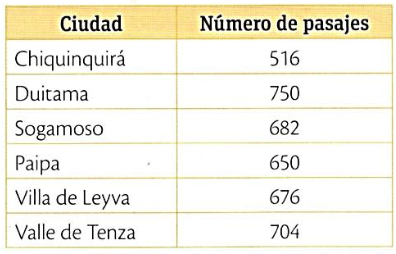
A partir de la información se puede afirmar que la moda de los datos es Duitama, por tener mayor frecuencia.

Ejercicio 3.

La edad (en años) de los primeros 30 visitantes a un parque de atracciones son las siguientes:
12, 13, 15, 16, 14, 13, 12, 13, 15, 18, 19, 12, 13, 14, 12, 17, 18, 14, 15, 14, 13, 12, 14, 12, 13, 14, 14, 14, 15, 15

Crea una tabla con las frecuencias absolutas y relativas (incluyendo las acumuladas). Calcula la moda.

Ejercicio 4. GENERALES

A. Las notas de los alumnos de una clase de Física fueron las siguientes:

7,7,6,10,1,4,5,5,3,9,5,5,8,6

a) Elabora una tabla de frecuencias
b) Calcula la media, moda y mediana

B. El número de talla de calzado de los alumnos de una clase es:

40, 41, 39, 38, 39, 38, 37, 41, 40, 42, 37, 38, 40, 39, 37, 38, 41, 39, 40, 36, 39, 40, 41, 38

Calcula media, moda y mediana