Grado 10 - Estadística - Periodo 3
- Tablas de frecuencia de datos agrupados
- Caracterización de datos y probabilidad.
- Tablas de contingencia.
- Probabilidad y conteo
- Probabilidad y conjuntos
- Probabilidad condicional.

Tablas de frecuencias datos NO agrupados
Usamos este tipo de tablas cuando tenemos variables cualitativas o cuantitativas con pocos valores.
Al ordenar los datos correspondientes a un cierto estudio, es usual agruparlos en clases o categorías, para lo cual, generalmente se utilizan tablas de frecuencias. Esta tabla está compuesta por las siguientes columnas:
- Valor de la variable: son los diferentes valores que toma la variable en estudio.
- Frecuencia Absoluta: Es el número de veces que aparece o se repite un cierto valor en la variable de medición.
- Frecuencia Absoluta acumulada: Representa el número de datos cuyo valor es menor o igual al valor considerado. Se obtiene sumando sucesivamente las frecuencias absolutas.
- Frecuencia relativa: Representa la razón de ocurrencia respecto al total. Se calcula como el cociente entre la frecuencia absoluta y el tamaño total de muestra.
- Frecuencia relativa acumulada: Corresponde a la suma de todas las frecuencias relativas da como resultado 1.
- Frecuencia relativa porcentual: Corresponde a la frecuencia relativa expresada en porcentaje. Se calcula como el producto de la frecuencia relativa multiplicada por 100.
- Frecuencia relativa porcentual acumulada: Corresponde a la suma de todas las frecuencias relativas
porcentuales da como resultado 100%.
EJEMPLO
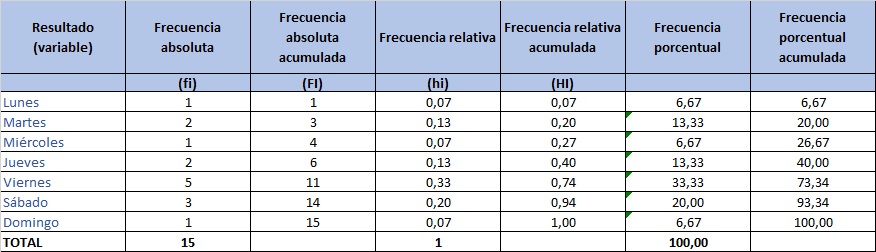
Se realiza una encuesta a jóvenes sobre el día de preferencia para ir al cine, sus respuestas fueron: martes,
jueves, viernes, sábado, sábado, domingo, viernes, jueves, lunes, miércoles, viernes, viernes, sábado,
viernes, martes. Con los resultados obtenidos anteriormente complete la tabla de frecuencia.
Observa el siguiente video:
1. CARACTERIZACIÓN DE DATOS Y PROBABILIDAD
A partir de la caracterización de datos estadísticos presentada en tablas de frecuencias, gráficos estadísticos o tablas de contingencia es posible calcular probabilidades y tomar decisiones.
Ejemplo 1.
Juan es el jefe de compras de la alcaldía de un municipio, él es encargado de realizar las compras para organizar
el kit escolar que se le entregará los estudiantes beneficiados de las escuelas públicas cada año. Dicha compra
debe hacerse por anticipación al inicio del año escolar, entre los elementos del kit están los buzos blancos para
el uniforme de diario. Para el siguiente año se beneficiaran 1250 estudiantes, Juan debe entonces, determinar
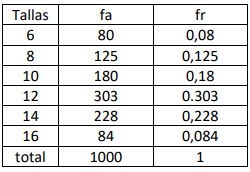
cuántos buzos de cada talla tiene que comprar, para ello cuenta con la relación de tallas correspondientes a los
1000 estudiantes beneficiados en el último año.


Tenga en cuenta que la frecuencia relativa de la distribución corresponde a la probabilidad de cada evento.
Ejemplo 2.
En el mes de octubre se efectuarán las elecciones para elegir el presidente de
la junta de acción comunal de un barrio, un habitante del barrio decide hacer
una encuesta a 120 vecinos habilitados para votar sobre el candidato de su
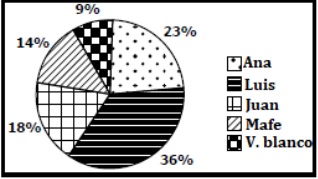
preferencia. El vecino presenta el resultado de su encuesta en un diagrama
circular.
Si se sabe que el vecino ha realizado un muestreo aleatorio entre los 600 habitantes del barrio habilitados para votar, que votación se esperaría para cada candidato el día de las elecciones?
En el diagrama circular se observan los porcentajes obtenidos para cada candidato, el cual corresponde a la probabilidad que tiene cada candidato de ganar, luego se determina la votación esperada para cada candidato entre los 600 vecinos habilitados.
Sea el evento A "El vecino seleccionado se inclina por Ana" 𝑃(𝐴) = 23%=0,23 entonces cantidad esperada de votos para Ana es
𝑃(𝐴) × 600 = 0,23 × 600 = 138. Se espera que 138 de 600 votos sean para Ana.
Sea el evento B "El vecino seleccionado se inclina por Luis"
𝑃(𝐵) = 36%=0,36 entonces cantidad esperada de votos para Luis es 𝑃(𝐵) × 600 = 0,36 × 600 = 216. Se espera que 216 de 600 votos sean para Luis.
Sea el evento C "El vecino seleccionado se inclina por Juan"
𝑃(𝐶) = 18%=0,18 entonces cantidad esperada de votos para Juan es 𝑃(𝐶) × 600 = 0,18 × 600 =108. Se espera que 108 de 600 votos sean para Juan.
Sea el evento D "El vecino seleccionado se inclina por Mafe"
𝑃(𝐷) = 14%=0,14 entonces cantidad esperada de votos para Mafe es 𝑃(𝐷) × 600 = 0,14 × 600 = 84. Se espera que 84 de 600 votos sean para Mafe.
Sea el evento E "El vecino seleccionado se inclina por voto en blanco"
𝑃(𝐸) = 9%=0,09 entonces cantidad esperada de votos para el voto en blanco es 𝑃(𝐸) × 600 = 0,09 × 600 = 54. Se espera que 54 de 600 votos sean para voto en blanco.
Ejemplo 3
35 estudiantes de un grado del colegio lagunilla fueron clasificados de acuerdo con la existencia de conectividad en su hogar y el cumplimiento en el envío de las actividades académicas. Los resultados se registraron en la siguiente tabla de contingencia:
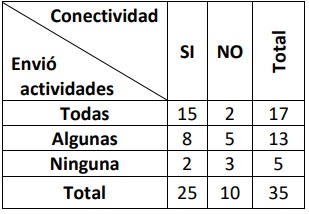
El director de grado decide rifar una Tablet entre sus 35 estudiantes. Cuál es la probabilidad de:
a. El ganador sea un estudiante que no tiene conectividad y no envió actividades. De los 35 estudiantes del grado hay 3 estudiantes que no tiene conectividad y no enviaron actividades. Por lo tanto
𝑃(𝐴) = 3/35 = 0,085 entonces la probabilidad es del 8,5%
b. El ganador sea un estudiante que no tiene conectividad De los 35 estudiantes del grado hay 10 estudiantes que no tiene conectividad. Por lo tanto
𝑃(𝐵) = 10/35 = 0,285 entonces la probabilidad es del 28,5%
c. El ganador sea un estudiante que envió todas las actividades De los 35 estudiantes del grado hay 17 estudiantes que enviaron todas las actividades. Por lo tanto
𝑃(𝐶) =
17/35
= 0,485 entonces la probabilidad es del 48,5%
Te invito a observar el siguiente video donde encontrarás más ejemplos:
ACTIVIDAD1. Resuelva cada uno de los ejercicios en forma ordenada
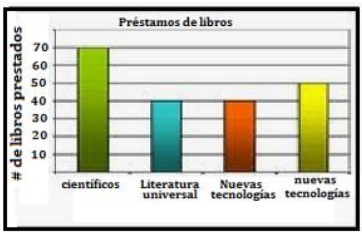
1. La bibliotecóloga de un colegio está proyectando las
compras de 1000 nuevos libros para el siguiente año,
para ello tiene en cuento los registros de préstamo
del último mes, los cuales se muestran en el siguiente
diagrama de barras. ¿Cuántos textos de cada clase se
debería comprar? Justifique el proceso utilizando
probabilidades
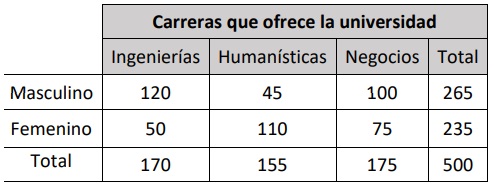
2. Una universidad realizó una reunión de
inducción a 500 jóvenes de grado undécimo,
con la idea de conocer cuál era la inclinación
profesional de los estudiantes y poder
ofrecerles sus servicios educativos. Los
siguientes son los resultados.
La universidad rifará una beca entre los 500
participantes. Hallar la probabilidad de que la
beca sea ganada por:
a. Un hombre que desee estudiar ingeniería
b. Una mujer que desea estudiar una carrera humanística
c. Una mujer
d. Un estudiante que desee estudiar una carrera de negocios
3. Teniendo en cuenta la situación anterior calcule la cantidad esperada de estudiantes en cada carrera para el siguiente semestre si la universidad tiene un cupo para 2500 estudiantes.
4. Proponga una situación de su contexto familiar, social o colegial relacionada con el tema trabajado en la guía
y resuelva
2. TABLA DE FRECUENCIAS DATOS AGRUPADOS
Usamos las tablas de frecuencias con datos agrupados cuando la variable toma un gran número de valores o es una variable continua. Para ello, se agrupan los diferentes valores en intervalos de igual amplitud, a los cuáles llamamos clases.
Pero antes de comenzar te voy a explicar los siguiente conceptos que se utilizan en la tabla de frecuencias:
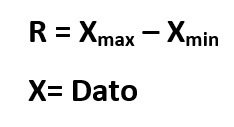
1. Rango: También se llama recorrido o amplitud total. Es a diferencia entre el valor mayor y el menor de los datos.
2. Número de Intervalos (K): Es el número de filas que vamos a calcular para registrar en la tabla. Para hallar este número empleamos la regla de Sturges, cuya fórmula es la siguiente:
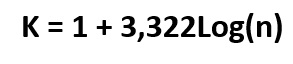
Donde n es el número de datos.
Nota: Si nos da una cifra decimal, aproximamos el dato entero al par más cercano
3. Amplitud (A): Son los rangos de números que vamos a agrupar en cada fila, este dato sale de dividir el rango entre el número de intervalos, es decir:
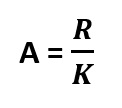
4. Marca de clase (A): Es la mitad de cada intervalo y se saca con el promedio.
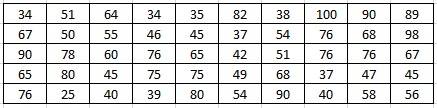
Ejemplo: Realizar la tabla de datos agrupados para los siguientes datos que es el peso que presentan los 40 estudiantes de la Institución Educativa el recuerdo:

Paso1. Sacamos el rango que es el dato mayor menos el dato mayor, que son 53 y 33:

Empleamos la fórmula:
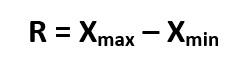
R = 53 -33
R = 20
Paso2. Sacamos el número de intervalos (K), que de acuerdo a la fórmula tenemos un n=40 estudiantes.
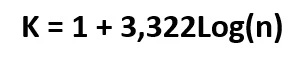
K = 1 + 3,322Log(40)
K = 6,32 * Aproximamos al impar más cercano, es decir 7.
Paso3. Sacamos la Amplitud (A). De acuerdo a la fórmula tenemos:
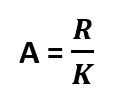
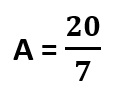
A = 2,85
A = 3, Siempre se aproxima al número siguiente para que quepan los números
Paso4.
a. Creamos una tabla con 7 filas y le agregamos 2 mas, es decir 9, una para los encabezados y otra para las sumatorias.
b. Creamos los intervalos de a 3 comenzando por el menor número, es decir 33:
Marca de clase
[33 - 36) (33+36)/2 = 34,5
[36 - 39) (36+39)/2 = 37,5
[39 - 42) (39+42)/2 = 40,5
[42 - 45) (42+45)/2 = 43,5
[45 - 48) (45+48)/2 = 46,5
[48 - 51) (48+51)/2 = 49,5
[51 - 54) (51+54)/2 = 52,5
Si nos damos cuenta, los números del lado izquierdo tienen intervalos abiertos, es decir, los números se incluyen y en los de la derecha son cerrados, por tanto no se incluyen en la sumatoria.
c. Creamos la frecuencia absoluta. Contamos los datos que están dentro de cada rango
Marca de clase Frecuencia Absoluta (f)
[33 - 36) 34,5 1
[36 - 39) 37,5 9
[39 - 42) 40,5 14
[42 - 45) 43,5 7
[45 - 48) 46,5 4
[48 - 51) 49,5 3
[51 - 54) 52,5 2
Sumatoria 40
d. Creamos la frecuencia absoluta acumulada. El cual suma el primer número de la frecuencia acumulada con el siguiente de la absoluta.
Marca de clase Frecuencia Absoluta Frecuencia abosoluta Frecuencia Relativa
(f) acumulada (F) fi
[33 - 36) 34,5 1 1 0,025
[36 - 39) 37,5 9 10 0,225
[39 - 42) 40,5 14 24 0,35
[42 - 45) 43,5 7 31 0,175
[45 - 48) 46,5 4 35 0,1
[48 - 51) 49,5 3 38 0,075
[51 - 54) 52,5 2 40 0,05
Sumatoria 40 1
e. Hallamos la frecuencia relativa (fi). Dividimos cada frecuencia abosula entre el número de datos, es decir 40.
d. Creamos la frecuencia relativa porcentual o porcentaje. Se saca multiplicando la frecuencia relativa por cien.
Marca de clase Frecuencia Absoluta Frecuencia abosoluta Frecuencia Relativa Porcentaje
(f) acumulada (F) fi %
[33 - 36) 34,5 1 1 0,025 2,5
[36 - 39) 37,5 9 10 0,225 22,5
[39 - 42) 40,5 14 24 0,35 35
[42 - 45) 43,5 7 31 0,175 17,5
[45 - 48) 46,5 4 35 0,1 10
[48 - 51) 49,5 3 38 0,075 7,5
[51 - 54) 52,5 2 40 0,05 5
Sumatoria 40 1 100
Sino entendiste la lectura te invito a observar el siguiente video:
Actividad 2. Realizar la tabla agrupada en intervalos de la velocidad a la que 50 conductores transitan por una avenida.