Grado 6 - Periodo 4
Geometría

TEMAS: SIMETRÍA Y TRANSFORMACIÓNES - FIGURAS 3D
Simetría y transformaciones
- Simetría de figuras geométricas
- Transformaciones (traslación, rotación, reflexión)
- Aplicaciones de las transformaciones
Introducción a la Geometría del Espacio
- Figuras tridimensionales básicas (cubos, prismas, pirámides)
- Reconocimiento y clasificación de figuras 3D
- Superficie y volumen de figuras tridimensionales.
DBA 5 . Propone y desarrolla estrategias de estimación, medición y cálculo de diferentes cantidades (ángulos, longitudes, áreas, volúmenes, etc.) para resolver problemas.
Estándar Básico de Competencia: Resuelvo y fórmula problemas que involucran relaciones y propiedades de semejanza y congruencia usando representaciones visuales.
Conocimientos previos: Perímetro, área y volumen
SIMETRÍA Y TRANSFORMACIONES
1. SIMETRÍA DE FIGURAS GEOMÉTRICAS
Una figura o forma tiene simetría, si se ve igual después de transformarse de alguna manera (por ejemplo, reflexión o rotación).
Está en todas partes a nuestro alrededor, y un concepto intuitivo: las diferentes partes de un objeto se ven iguales de alguna manera. Pero usando transformaciones, podemos dar una definición matemática mucho más precisa de lo que realmente significa la simetría:
1.1. Simetría reflexiva

Una forma tiene simetría de reflexión si se ve igual después de ser reflejada.
Si se ve igual después de reflejarse. La línea de reflexión se llama eje de simetría
Si una forma tiene simetría de reflexión, el eje de simetría es la línea que la divide en dos mitades iguales y divide la forma en dos mitades. Algunas figuras también pueden tener más de un eje de simetría.

Te invito a observar el siguiente video sobre simetría:
1.2. Simetría rotacional
La simetría rotacional (también llamada reflexión, u simetría axial, radial o cilíndrica) está presente cuando una figura se puede girar (menos que 360°) de tal manera que parece que no se rotó (permaneció igual). El centro de rotación es el punto alrededor del cual se gira una figura de tal manera que se mantiene la simetría rotacional.

La primera pregunta es, ¿cuantas veces tenemos que rotar la figura para que conserve su posición inicial?
Para la H, podemos girarlo dos veces, el triángulo puede girarse 3 veces y aun así verse igual y el hexágono se puede girar 6 veces.
¿Y si tuvieras una estrella de seis puntas y giraras esa estrella menos de 360°? Si la estrella rotada se veía exactamente igual que la estrella original, ¿qué diría eso de la estrella?
La segunda pregunta es ¿cuantos grados debemos rotar la figura?
Para la H, se realizaron rotaciones de 180°, el triángulo rotó 120° y el hexágono realizó rotaciones de 60°.
Como se ¿cuantos grados tengo que rotarlo?
Dividimos 360° entre el número de lados que tiene la figura.
Ejemplo:
Determinar si la siguiente figura tiene simetría rotacional. Encuentra el ángulo y cuántas veces se puede girar.

Solución:
El pentágono se puede girar 5 veces. Debido a que hay 5 líneas de simetría rotacional, el ángulo sería:

Te invito a observar el siguiente video sobre simetría axial y central
Actividad 1:
1. Determinar cuántas veces se pueden girar las siguientes figuras hasta su posición inicial y cuantos grados se debe rotar:
- Si una figura tiene 3 líneas de simetría rotacional, se puede girar _______ veces.
- Si una figura se puede rotar 6 veces, tiene _______ líneas de simetría rotacional.
- Si una figura se puede girar n veces, tiene _______ líneas de simetría rotacional.
- Para encontrar el ángulo de rotación, divídalo 360° por el número total de _____________.
- Cada cuadrado tiene un ángulo de rotación de _________.
3. Determinar si cada declaración es verdadera o falsa.
Cada paralelogramo tiene simetría rotacional.
Cada figura que tiene simetría lineal también tiene simetría rotacional.
4. Determinar si las siguientes palabras tienen simetría de rotación.
- OHIO
- MOW
- WOW
- KICK
- pod
TRANSFORMACIONES (traslación, rotación, reflexión)
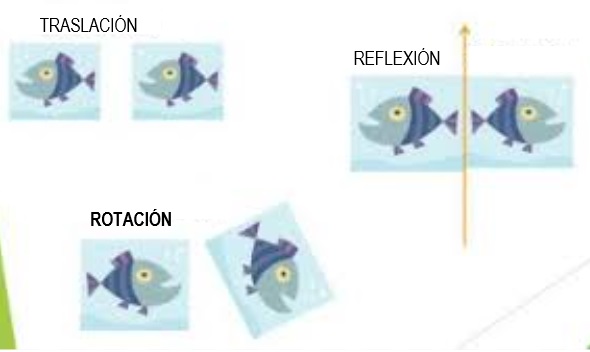
Una transformación es una operación que mueve, voltea o cambia de otra manera una figura para crear una nueva figura.
Transformación Rígida:
Una transformación rígida (también conocida como transformación de isometría o congruencia) es una transformación que no cambia el tamaño o la forma de una figura.
Las transformaciones rígidas son traslaciones, reflexiones y rotaciones. La nueva figura creada por una transformación se llama la imagen. La figura original se llama la preimagen. Si la preimagen es A, entonces la imagen sería A′. Si hay una imagen de A′, eso sería etiquetado A′′ y así sucesivamente.
Traslación:
Una traslación es una transformación que mueve cada punto de una figura a la misma distancia en la misma dirección.
Por ejemplo, esta transformación mueve el paralelogramo hacia la derecha 5 unidades y hasta 3 unidades. Está escrito (x,y)→(x+5,y+3)(x,y)→(x+5,y+3).

Te invito a observar el siguiente video sobre traslación:
Estos son algunos ejemplos gráficos de traslación:
De igual manera te invito a que practiques a través de Geogebra:
Actividad 2:
1. En el mismo link del ejercicio anterior desarrolla la actividad que dice "Ahora te toca a ti" de acuerdo a la dirección del vector:
2. Escribe en tu cuaderno y contesta la pregunta:
Define con tus palabras que entiendes por traslación y especificamente traslación de figuras planas en el plano cartesiano.
ROTACIÓN
La rotación consiste en girar o rotar una figura alrededor de un punto fijo llamado CENTRO DE ROTACION. Para girar una figura se debe conocer el centro de rotación y el sentido (el sentido positivo o a la izquierda o sentido negativo hacia la derecha).
EJEMPLO 1:

EJEMPLO 2:

Te invito a observar el siguiente video sobre rotación:
Actividad 3:
1. Escribe cuál es el centro de rotación, el sentido de rotación y las nuevas coordenadas de rotación de cada figura (desarrollo en el cuaderno):

2. Ubica las coordenadas de la siguiente figura antes y después de la rotación. Colorea cada figura de un tono diferente.

REFLEXIÓN
La reflexión de una figura es una nueva figura que resulta de "voltear" la figura original sobre una línea llamada eje de reflexión. Cada punto de la figura original se corresponde con un único punto en la figura reflejo y viceversa

Eje de Reflexión: Es una línea imaginaria alrededor de la cual una figura puede ser reflejada. Los puntos reflejados siempre están equidistantes del eje de reflexión. Esta linea puede ser horizontal, vertical, diagonal u oblicual

Trabajando la reflexión en un plano cartesiano encontramos que las figuras pueden ser reflejadas como un espejo en el 1, 2, 3 o 4 cuadrante

Comparemos algunos de los vértices. En la figura de ABAJO las coordenadas para el vértice superior izquierdo de la figura original son (-5, 5). Al reflejar la figura sobre el eje y− las coordenadas del vértice correspondiente son (-5, -5).

¿Cuáles son las coordenadas del vértice inferior derecho? Las coordenadas originales son (-1, 1) y luego de reflejarla las coordenadas cambian a (-1, -1). Como puedes apreciar solo las coordenadas de x− cambian. De hecho, las coordenadas de y− se convierten en enteros negativos de las originales Esto indica que se trata de una reflexión vertical (arriba/abajo) o una reflexión sobre el eje de simetría x− .
En una reflexión horizontal (izquierda/derecha) o una reflexión sobre el eje y− las coordenadas de x− cambian a enteros negativos. Veamos el siguiente ejemplo:

Esta es una reflexión sobre el eje x− Compara los puntos. Notas como las coordenadas de y− se mantienen iguales. Las coordenadas de x− se convierten en enteros negativos de las originales. Mira la punta superior del triángulo, por ejemplo. Las coordenadas del punto original son (-4, 6) y las coordenadas del punto nuevo son (4, 6). La coordenada x− cambió de -4 a 4.
Te invito a observar el siguiente video sobre el tema:
Nota: invito a docentes y estudiantes para que lleven a clase un espejito para que observen como se refleja la imagen en los diferentes ejes.
Actividad 4:
Intenta realizar este ejercicio por tu cuenta en el cuaderno.
Dibuja una reflexión de la figura sobre el eje x− en un color diferente.

Introducción a la Geometría del Espacio
Reconocimiento y clasificación de figuras 3D
Observe las siguientes imágenes; en cada una de ellas hay cuerpos geométricos que acostumbramos ver día a día:

Volumen de cuerpos geométricos
CUBO
El volumen de un cubo es la cantidad de espacio que ocupa y su medida es el número de unidades cúbicas que ''cabrían'' en ese espacio. Para calcular el volumen de un cuerpo en el espacio lo comparamos con un cubo cuya arista mide 1 unidad

En las imágenes puede observar cuerpos geométricos de volumen 8 unidades cúbicas, pues están formados por 8 cubos de arista 1 unidad.
Estas 4 figuras se encuentran en 3 dimensiones ya que tienen un ancho (Profundidad), un alto y largo. Observa los números que se encuentran en cada una de sus dimensiones.

Cubo o hexaedro regular es un poliedro limitado por seis caras cuadradas congruentes. Es uno de los denominados sólidos platónicos. Un cubo, además de ser un hexaedro (6 lados), puede ser clasificado también como paralelepípedo recto y rectangular, pues todas sus caras son cuadradas y paralelas dos a dos.
¿Cómo se calcula el volumen de un cubo?
El volumen de un cubo es igual a la medida de su lado al cubo. Es decir:
Volumen = lado x lado x lado =lado3
Es muy importante saber las unidades de medida e indicar que estas están elevadas al cubo.
¿Para qué nos sirve saber el volumen de un cubo?
Es importante porque gracias al volumen podremos saber la capacidad de un recipiente. En este caso, la de un cubo.
Ejemplo:
Si nuestro cubo tiene de lado 5 dm.
Volumen = 5 x 5 x 5 = 53 = 125 dm3
Si hacemos la conversión y sabemos que:
1 litro = 1 dm3
Entonces en nuestro cubo caben 125 litros.

Para reforzar el tema sobre el volumen de un cubo te invito a observar el siguiente video:
Área del cubo
El área del cubo corresponde a la suma de las áreas de todas sus caras. Para calcular el área de un cubo multiplicas el área de una cara por 6, ya que tienes 6 caras cuadradas y todas congruentes entre sí.
Ejemplo 1:
Calcular el área de un cubo cuya arista mide 5 cm

Solución:
1° Calcular el área de una de las caras del cubo.

2° Multiplica el área de una cara por 6, ya que el cubo tiene 6 caras congruentes.
Luego. El área del cubo es 6 X 25 cm2 = 150 cm2
Ejemplo 2:
Determina la medida de las aristas de un cubo cuya área es 96 cm2
1° Calcula el área de cada cara del cubo Al dividir el área del cubo por 6, obtienes el área de una cara.
96 cm2 : 6 = 16 cm2
2° Determina la medida de los lados de una cara del cubo.
Como cada cara del cubo es un cuadrado, los lados miden 4 cm, ya que 4cm X 4cm = 16 cm2 Luego, la arista del cubo mide 4 cm
Te invito a reforzar el tema con el siguiente video:
Actividad 5:
Responde en tu cuaderno:
1. Calcula el área de los siguientes cubos

2. Determina la medida de la arista de cada cubo dada su área (A)

3. Resuelve los siguientes problemas.
a. El área total de la red de un cubo es 54 m2 , ¿cuánto mide su arista?
b. Si el área de una de las caras de un cubo mide 25 m2 , ¿cuál es el área de su red de construcción?
c. La arista de un cubo mide 5,8 cm, ¿cuál es su área?
d. El área de una de las caras de un cubo es de 64 cm2 , ¿cuál es el área del cubo?
e. Con un litro de pintura se pueden pintar 18 m2 . Si una caja de forma cúbica tiene una arista de 1 m, ¿cuántos litros se necesitan para pintar 25 de estas cajas?
4. Hallar el volúmen y área de las siguientes figuras:


PRISMA
Son sólidos geométricos donde dos de sus caras se llaman bases. Sus caras laterales son regulares.

De acuerdo a sus bases existen diferentes tipos de prismas de acuerdo a la figura que forme:

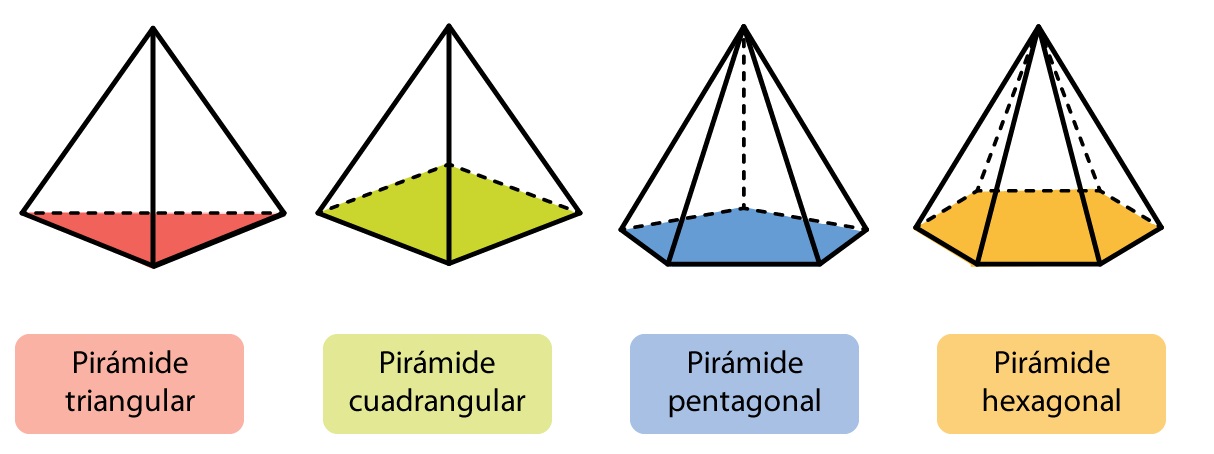
PIRÁMIDE

Es un poliedro, constituido por un polígono simple de base y cuyas caras laterales son triángulos que se juntan en un vértice común, también llamado ápice o cúspide. Los triángulos se denominan caras laterales.
Actividad 6:
1. Responde las preguntas de la siguiente actividad interactiva:
https://wordwall.net/es/resource/8319727/prismas-y-piramides
2. Responde las preguntas de la siguiente actividad interactiva:
https://wordwall.net/es/resource/27752528/prismas-y-piramides
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad: