Grado 6 - Periodo 2
Geometría
Temas:
Polígonos: Elementos de un polígono - Clasificación de polígonos - Polígonos regulares e irregulares
Triángulos: Tipos de triángulos según sus lados y ángulos - Propiedades y clasificación - Perímetro y área de triángulos
DBA 6. Representa y construye formas bidimensionales y tridimensionales con el apoyo en instrumentos de medida apropiados.
Estándar básico de competencia:
- Represento objetos tridimensionales desde diferentes posiciones y vistas.
- Clasifico polígonos en relación con sus propiedades.
Conocimientos previos: Manejo del transportador y el compás
POLÍGONOS

1. ELEMENTOS DE UN POLÍGONO:
Un polígono es una figura geométrica plana cerrada, formada completamente por segmentos de línea que se intersecan en sus extremos, formando vértices. A estos segmentos de línea se les llama lados.
Los polígonos pueden tener cualquier cantidad de lados y ángulos, pero sus lados nunca pueden ser curvos. La manera más fácil de identificar un polígono es viendo si es una figura cerrada sin lados curvos. Si existe alguna curvatura en la figura, no puede ser un polígono.
Si buscamos el origen de la palabra "polígono" esta se forma por dos voces de origen griego:
• "polys": muchos
• "gonía" : ángulos; por lo tanto, es una figura con varios ángulos.
Otra definición también aceptada para este término puede ser "poligonal cerrada".
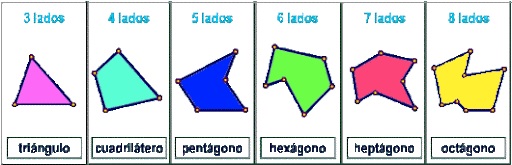
El polígono más pequeño es el triángulo, que tiene tres lados y tres ángulos.

Mientras que el polígono de más lados, puede tener tantos lados como tu imaginación alcance a crear.
El polígono es la frontera que separa al plano en dos regiones:
- Una que está dentro, llamada región interior del polígono
- y una exterior, llamada región exterior del polígono. El plano es la unión de estos tres subconjuntos.
Un polígono está formado por elementos básicos:
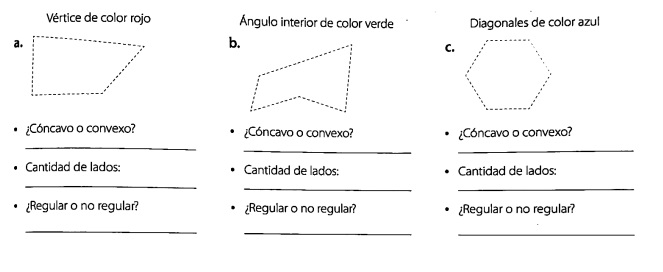
1. Vértice : es el punto donde se intersecan dos segmentos contiguos. Se designan con una letra mayúscula A, B, C, D…
2. Lados: es cada uno de los segmentos de recta que forman el polígono. Se designa con dos letras mayúsculas ubicadas en sus extremos, o con una letra minúscula en correspondencia con el vértice opuesto: AB = d, BC = e , CD = a, DE = b, EA = c
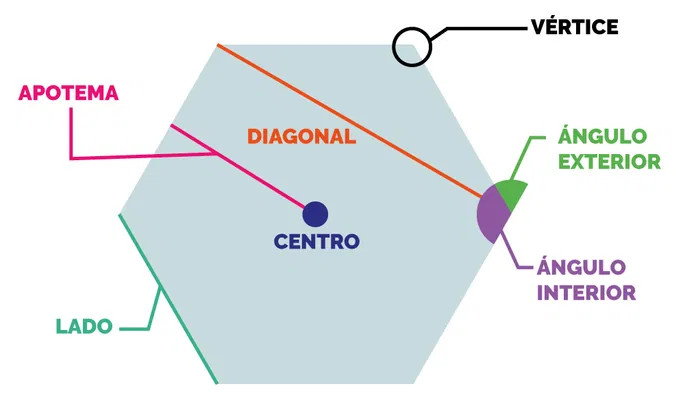
3. Ángulo interior: es el ángulo formado por dos lados del polígono. El ángulo interior se designa con una letra griega o con las tres letras mayúsculas de los vértices que correspondan.
4. Angulo exterior: es el ángulo formado por un lado y la prolongación de otro contiguo hacia la región exterior. Generalmente se designa con la letra griega del ángulo interior adyacente acompañada de un subíndice
5. Diagonal: es el trazo que une dos vértices no consecutivos del polígono. Se designa con las dos letras mayúsculas correspondientes a los vértices que se unen, o por una letra d con subíndice: AC =d 1, AD=d2.
6. Apotema de un polígono regular: La apotema de un polígono regular es el segmento perpendicular a un lado desde el centro del polígono. Es básica para conocer el área del polígono ya que es la altura de cada uno de los triángulos formados por cada dos radios y el lado.
2. CLASIFICACIÓN DE POLÍGONOS:
2.1. CANTIDAD DE LADOS:
Los polígonos pueden ser clasificados utilizando distintos criterios, uno de ellos es contando la cantidad de lados que este posea.

2.2. TIPO DE ÁNGULO
Otra clasificación que se puede hacer de los polígonos es según el tipo de ángulos que los componen.
- Polígonos convexos
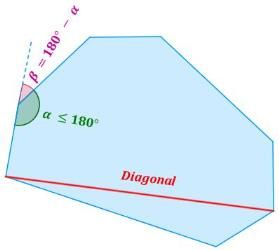
Todos sus ángulos internos son menores (o iguales) a 180°. (La suma de los ángulos internos de un polígono convexo se halla con la fórmula de los ángulos internos de un polígono). Todas sus diagonales son internas al polígono en todos sus puntos.
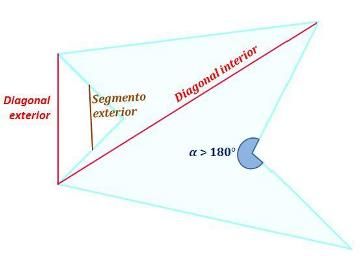
- Polígonos cóncavos es un polígono con uno o más ángulos interiores de más de 180º.
2.3. LONGITUD DE SUS SEGMENTOS (LADOS)
"polígonos regulares" todos sus ángulos y lados son iguales y

"polígonos irregulares". No cumple con al menos una de las características anteriores.
Te invito a observar el siguiente video de acuerdo a la clasificación de los polígonos de acuerdo a sus ángulos y lados
Actividad 1.
1. Identifica cada elemento en los polígonos y márcalos con el color indicado. Luego, completa lo solicitado
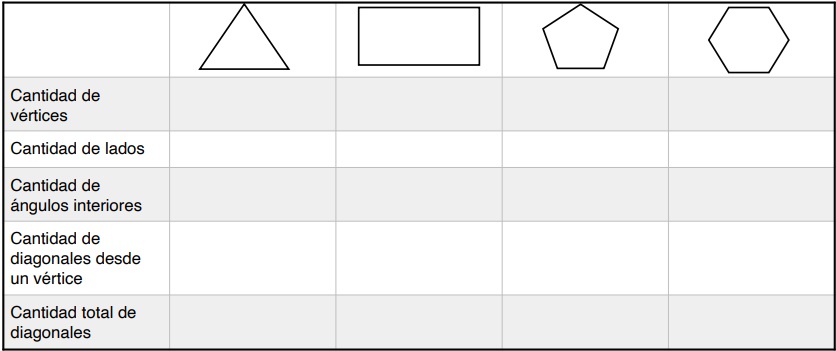
2. Interpreta la información de la tabla. Luego, complétala y responde.
TRIÁNGULOS
Un triángulo se define como un polígono, es decir, una figura geométrica plana compuesta por tres lados, tres ángulos y tres vértices. Entre los tres ángulos, suman 180º. Los vértices son los puntos comunes que hay a cada par de lados.
1. TIPOS DE TRIÁNGULOS SEGÚN SUS LADOS Y ÁNGULOS
1.1. SEGÚN SUS LADOS
Según sus lados podemos distinguir tres tipos de triángulos:
Triángulo equilátero: tiene sus tres lados iguales, todos miden lo mismo.
El triángulo isósceles: tiene dos lados iguales y uno distinto.
El escaleno: tiene los tres lados diferentes, es decir, de distinta longitud.
Puedes comprobarlo en la siguiente imagen.

1.2. SEGÚN SUS ÁNGULOS
Existen tres tipos de triángulos según sus ángulos:
Triángulo rectángulo: en él dos de sus lados forman un ángulo recto, o lo que es lo mismo, tiene un ángulo de 90º.
Triángulo acutángulo: cuando todos sus ángulos miden menos de 90º, es decir, son ángulos agudos.
El triángulo obtusángulo: cuando dos de sus lados forman un ángulo obtuso, o lo que es lo mismo, cuando tiene un ángulo de más de 90º.
A continuación puedes verlo en la imagen.

Analiza con mucha atención la siguiente tabla donde se resumen las características de los triángulos

Te invito a observar el siguiente video para reforzar el tema:
Actividad 2:
1. Identifica los siguientes triángulos, a partir de las características que se describen


2. Responde las preguntas del siguiente enlace:
PROPIEDADES DE LOS TRIÁNGULOS
Los triángulos son el polígono con el número más bajo de lados y ángulos, motivo por el cual se consideran como figuras bastante básicas, pero en realidad tienen numerosas propiedades.
Aquí te dejamos un repaso a las principales propiedades de los triángulos:
En primer lugar, los triángulos siempre tienen
tres ángulos interiores que, si los sumamos, siempre da 180º.

2. Es el único polígono que no posee diagonales.

3. Todos los polígonos que no son triángulos se pueden subdividir en este primer tipo. Es decir, un pentágono se puede subdividir en triángulos, también un hexágono puede subdividirse en triángulos, etc. La manera más sencilla de hacerlo es trazando las diagonales del polígono en cuestión.

4. Por lo menos dos de los tres ángulos de un triángulo son agudos siempre.

Gracias a la trigonometría, podemos aplicar las propiedades de los triángulos al estudio de los demás polígonos porque, como ya hemos dicho, cualquier polígono puede dividirse en triángulos.
Es importante recordar que hay distintos tipos de triángulos, por lo que las propiedades pueden ser específicas.
Por ejemplo, el triángulo equilátero tiene los tres lados de la misma longitud y los tres ángulos de la misma amplitud (60º). Por otro lado, el triángulo rectángulo tiene una propiedad muy especial que es que puede aplicarse el Teorema de Pitágoras, que relaciona sus tres lados (hipotenusa al cuadrado es igual a la suma de cada uno de los catetos al cuadrado).
En esta gráfica resumimos las propiedades:

PERÍMETRO Y ÁREA DE TRIÁNGULOS
1. Perímetro
El perímetro de un triángulo es igual a la suma de sus tres lados.

2. Área
El área de un triángulo es igual a base por altura partido por 2 .
La altura es la recta perpendicular trazada desde un vértice al lado opuesto (o su prolongación).

El área de un triángulo equilátero, como en todo triángulo, será un medio de la base (a) por su altura. El triángulo equilátero tiene los tres lados iguales. En este caso, el área viene definida por la siguiente fórmula:


¿Cómo se obtiene?
El área de un triángulo equilátero se obtiene como el producto de la base (el lado a) por la altura (h) dividido por dos (Nota: ¿por qué el área de un triángulo es un medio del producto de la base por la altura?).
Veamos cual es la altura del triángulo equilátero.
Ésta se puede calcular a partir del teorema de Pitágoras. Los lados a, a/2 y h forman un triángulo rectángulo. Los lados a/2 y h son los catetos y a la hipotenusa.

Aplicando el teorema de Pitágoras:

Obtenemos que la altura (h) del triángulo equilátero es:

Ahora, aplicando que el área es un medio del producto de la base (a) por la altura (h):

Y llegamos a que la fórmula del área del triángulo equilátero es:

Siendo a el lado del triángulo
Ejemplo1 triángulo equilátero:
Sea un triángulo equilátero con todos los lados iguales de longitud a=5 cm.

¿Cuál es su área?
Según la fórmula anterior, quedaría de la siguiente manera:

Ejemplo2 triángulo isósceles:
Hallar el área del siguiente triángulo:

Ejemplo3 triángulo rectángulo
Calcular el área del triángulo rectángulo cuyos catetos miden 3 y 4 cm:

Puedes ver la tabla de fórmulas del área del triángulo. Dependiendo del tipo de triángulo puedes necesitar un elemento (triángulo equilátero), dos (base y altura) o tres (siempre que no sean los tres ángulos.

Actividad 3.
Contesta en tu cuaderno:
1. Calcula el o los ángulos que faltan en los siguientes triángulos (tienes que dibujarlo con un transportador):
- Un triángulo con un ángulo de 65º y otro de 15º.
- Un triángulo rectángulo con un ángulo de 20º.
- Un triángulo equilátero.
2. ¿Es posible que un triángulo sea equilátero y a la vez rectángulo? Justifica tu respuesta.
3. ¿Cuántas diagonales tiene un triángulo
4. Halla y selecciona el resultado correcto de los siguientes ejercicios:


HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION: Onceava Semana del Periodo
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
ACÁ PUEDES DESCARGAR LA GUÍA
ACUERDOS PEDAGÓGICOS
RÚBRICA
Rúbrica para polígonos:
Rúbrica para triángulos:






