GEOMETRÍA
Grado 6 - Periodo 1

LOGRO. Comprender algunos conceptos y procedimientos de la geometría básica aplicaciones para interpretar y transmitir diversas información del entorno
DBA4. Utiliza y explica diferentes estrategias (desarrollo de la forma o plantillas) e instrumentos (regla, compás o software) para la construcción de figuras planas y cuerpos.
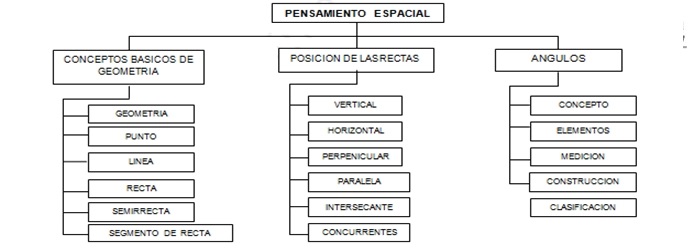
TEMAS (Pensamiento Espacial)
CURIOSIDADES MATEMÁTICAS
Las 10:08 y las 10:10 en los relojes

¿Te has fijado alguna vez en que casi todos los relojes que aparecen en los anuncios marcan las 10:10 o las 10:08? Si nunca lo has hecho, puedes comprobarlo por ti mimo, busca cualquier anuncio.
¿A qué se deben estas horas tan parecidas? Pues en definitiva a diversos efectos psicológicos y estéticos muy estudiados:

- Las manillas forman un "tick" o "check", que significa "aceptable" u "ok". También puede identificarse la posición de las manillas como una sonrisa.
- La posición de las agujas no tapa ni el logo del fabricante ni el calendario, ubicado normalmente a las 9 (cuando está a la izquierda) o a las 3 (cuando se sitúa a la derecha).
- La gente se suele levantar a las 10 de la mañana cuando no tiene que ir a trabajar porque es fin de semana o festivo. En el caso del reloj Casio de la derecha de la imagen podemos ver que el día está fijado como "SUN" (domingo) y que el calendario marca el 30 de junio, para muchos, el comienzo de las vacaciones. Este mensaje subliminal crea una sensación agradable en el posible comprador.
- Si hay segundo , éste suele señalar los 25 ó 35 segundos . Si marcara los 30 segundos dividiría la circunferencia en tres partes iguales, dando una sensación rígida y puramente matemática. Así consigue romperla.
- Y estos sólo son algunos de los motivos de por qué los publicistas eligen fotografiar los relojes a las 10:08 ya las 10:10. No te parece genial, ¿que las matemáticas se utilizan en todo?
HISTORIA DE LA GEOMETRÍA
La geometría es una de las ciencias más antiguas. Inicialmente, constituía un cuerpo de conocimientos prácticos en relación con las longitudes, áreas y volúmenes. En el antiguo Egipto estaba muy desarrollado, según los textos de Heródoto , Estrabón y Diodoro Sículo . Euclides , en el siglo III a.C.

Euclides dedicó gran parte de sus libros a la geometría (¡a los griegos les encantaba!). Su obra sobre esta disciplina perduró casi intacta hasta el siglo XIX y lo que se hizo después ya pertenece a las matemáticas avanzadas, las que se estudian en la universidad. Así que prácticamente todo lo que estudiamos hoy en el colegio de geometría se escribió ¡hace más de dos mil años! Es por eso que la geometría plana y del espacio se suele llamar Geometría Euclídea.
Te invito a observar el siguiente video para reforzar el tema:
GEOMETRIA
1. CONCEPTOS
La geometría como palabra tiene dos raíces griegas: GEO = tierra y metrón = medida; o mar, significa "medida de la tierra".

2. PUNTO, LÍNEAS Y RECTAS
2.1. Punto.
Un punto se define como una ubicación en cualquier espacio y se representa como "." No tiene dimensión, longitud, área, volumen, ni otro ángulo dimensional. Marca el comienzo para dibujar cualquier figura o forma y suele rotularse con letras mayúsculas.
2.2. Línea
Cualquier línea está compuesta por puntos, que es la unidad gráfica mínima.
Una serie de puntos que se sitúan uno junto al otro dan lugar a un trazo continuo, al que llamamos línea.
2.3. Línea recta
Es una sucesión de infinitos puntos (no tiene principio ni fin, es decir, no tiene límites) en la que los puntos están trazados en una misma dirección. Cuando los puntos siguen siempre la misma dirección, forman una línea recta.
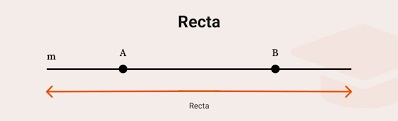
(Para que sea una verdadera línea recta no podría terminar nunca, tendría que ser infinita, por la izquierda y por la derecha.)
Las líneas rectas son infinitas, por lo que nunca podremos pintar una línea recta completa, solo un trocito, el resto tendremos que imaginarlo.
2.4. Segmento de recta:
Es la partición por la izquierda y derecha de una recta. Para nombrar cualquier segmento de recta, utilizamos letras mayusculas, por ejemplo:

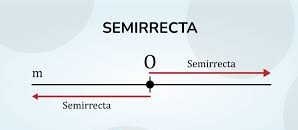
2.5. Semirecta:
Cuando se hace una sola partición a una recta se forman dos semirrectas
2.6. Línea curva
Es una sucesión de infinitos puntos que cambian continuamente de dirección.
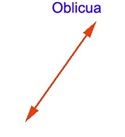
2.7. Línea oblicua
Oblicuo es un adjetivo que refiere a inclinado.
Una línea o recta oblicua es aquella que, al intersecar otra recta, crea un ángulo que no mide 90º (es decir, no se trata de un ángulo recto). Los ángulos creados por las rectas oblicuas, por otra parte, no son iguales (no miden lo mismo).
2.8. Línea quebrada
Es una línea que sin ser recta está formada por varios segmentos de recta. De esta manera, el extremo de cada segmento es el inicio del siguiente, con excepción del último.
Si la línea quebrada se cierra coincidiendo el origen con el final se forma un polígono.

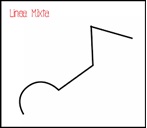
2.9. Línea mixta:
Son aquellas que combinan tanto líneas rectas como curvas en una misma composición. Estas l líneas pueden ser utilizadas para crear contrastes interesantes y agregar dinamismo a una obra.
2.10. Línea ondulada:
Describe una dirección cambiante, esta última cambia mediante arcos de circunferencias que se entrelazan mediante tangencias.

CLASIFICACIÓN POR LA POSICIÓN QUE TIENEN EN EL ESPACIO
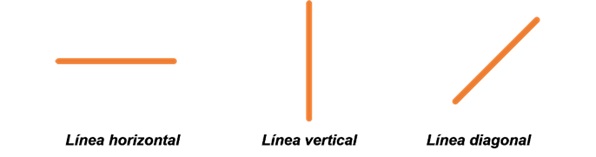
1. Línea vertical: : sigue la dirección de arriba abajo.
2. Línea horizontal:: coincide con el horizontal.
3. Línea diagonal:: es cualquier recta que no es ni vertical ni horizontal.
RELACIÓN QUE GUARDAN ENTRE SÍ
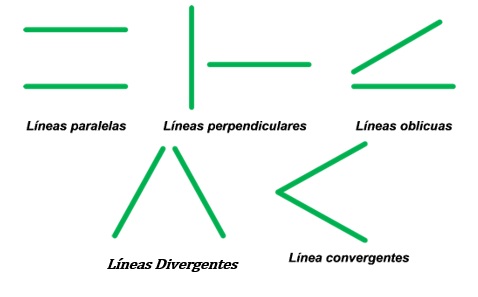
1. Líneas paralelas :: siguen la misma dirección y aunque se prologuen, nunca llegan a intersectarse.
2. Líneas perpendiculares :: forman un ángulo recto entre sí.
3. Líneas oblicuas:: son aquellas que no son paralelas ni perpendiculares.
4. Líneas convergentes:: son aquellas líneas oblicuas que en un determinado punto se unen entre sí.
5. Líneas divergentes: : son aquellas líneas oblicuas que inician en un mismo punto y en algún punto de su trayecto se desvían separándose entre sí.
LÍNEAS DE ACUERDO A SU INICIO Y SU FIN
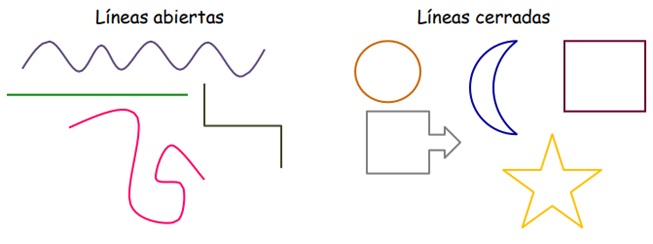
1. Líneas abiertas :: Termina en un lugar diferente a donde inició
2. Líneas Cerradas :: Tiene su inicio y
fin en un solo punto
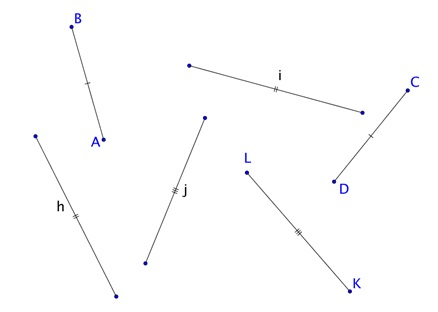
CONGRUENCIA DE SEGMENTOS
Cuando dos segmentos tienen la misma longitud se dicen que son congruentes. Se usa el símbolo:


NOTA: Para representar que dos
segmentos no son congruentes se usa el mismo símbolo, pero tachado:
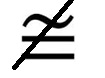
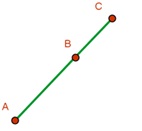
SEGMENTOS CONSECUTIVOS: Cuando dos segmentos comparten únicamente un punto extremo, se denominan segmentos consecutivos
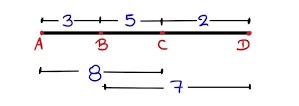
SEGMENTOS COLINEALES: Si los segmentos pertenecen a una misma recta (están sobre ella), se dicen que son segmentos colineales
SEGMENTOS NO COLINEALES: si no está sobre la misma recta, se dicen no colineales.
Practica en el siguiente link: https://edu.gcfglobal.org/es/geometria-basica/segmentos/1/
PUNTOS COLINEALES
Imagina tres puntos en un plano, si existe una recta que los contiene, se dice que son puntos colineales. Cuando hay más de tres puntos este concepto también se aplica. Es decir, uno o más puntos pueden ser o no colineales.
En el siguiente interactivo puedes observar los puntos A, B y C.
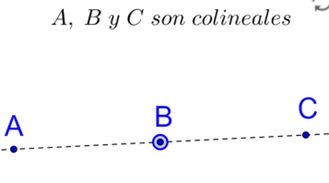
Cámbialos de posición para establecer si son o no puntos colineales. Cuando estén alineados podrás apreciar la recta que los contiene:
Practica en el siguiente link: https://edu.gcfglobal.org/es/geometria-basica/posicion-relativa-de-puntos/1/
ACTIVIDAD 1:
- Realiza el ejercicio interactivo en la siguiente página y enséñale los resultados a tu docente: https://www.liveworksheets.com/es/w/es/matematicas/1851556
- Realiza el ejercicio interactivo en la siguiente página y enséñale los resultados a tu docente: https://www.liveworksheets.com/es/w/es/matematicas/127141
ANGULOS
Un ángulo es la región del plano comprendida entre dos semirrectas con origen común.
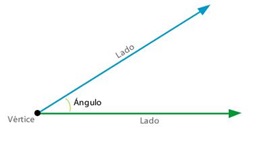
- A las semirrectas se las llama lados del ángulo.
- El origen común es el vértice
CLASIFICACION
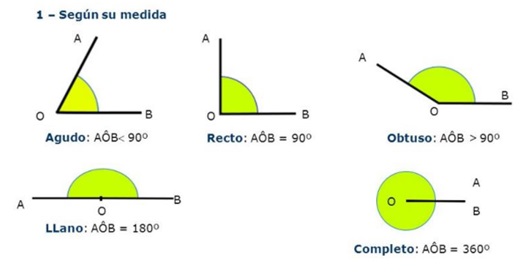
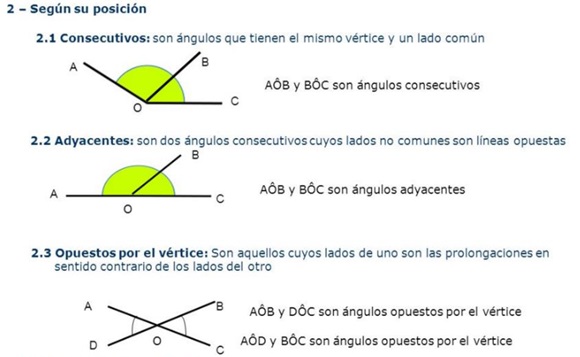
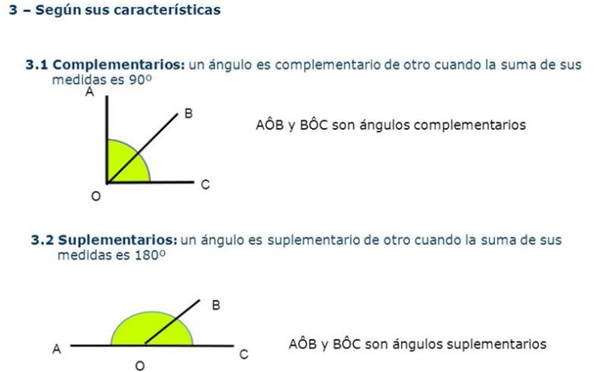
Te invito a observar el siguiente video sobre el manejo del transportador y la medición de ángulos
ACTIVIDAD 2:
1. Medir cada de los siguientes ángulos y clasificarlos en agudos u obtusos.
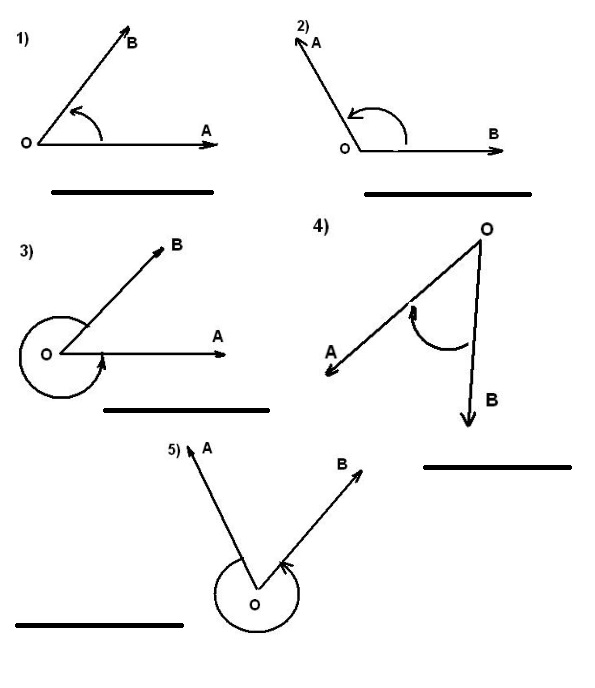
2. La medida del ángulo que se forma entre el minutero y el horario de un
reloj a las 3:00 horas es:
A. 60°
B. 90°
C. 120°
D. 180°
3. Un ángulo es la abertura formada por dos…
A. Líneas rectas
B. Ángulos
C. Semirrectas
D. Triángulos
4. Un ángulo llano mide:
A. 0°
B. 90°
C. 180°
D. 360°
5. El instrumento utilizado para medir ángulos es:
A. El metro
B. El transportador
C. El compás
D. La escuadra
6. Si el doble la medida de un ángulo equivale a un ángulo recto, la medida del ángulo es:
A. 30°
B. 45°
C. 90°
D. 180°
7. Los ángulos están formados por
A. Un vértice y dos lados
B. Dos vértices y dos lados
C. Un vértice y tres lados
D. Tres vértices y dos lados
8. Los ángulos cuya medida se encuentra entre 0° y de 90º se llaman:
A. Ángulos planos
B. Ángulos rectos
C. Ángulos agudos
D. Ángulos nulos
9. Los ángulos cuya medida se encuentra entre 90° y de 180º se llaman:
A. Ángulos planos
B. Ángulos rectos
C. Ángulos agudos
D. Ángulos obtusos
10. ¿Cuántos ángulos determinan dos semirrectas con origen común?
A. Uno
B. Dos
C. Tres
D. Cuatro
11. En el sistema sexagesimal:
A. Todos los ángulos miden 60°
B. Hay sesenta ángulos diferentes.
C. La circunferencia se divide en 180 grados.
D. El ángulo recto mide 90°.
12. Si estas mirando al sur y giras un ángulo llano. Donde miras después del giro.
A. Oriente
B. Occidente
C. Norte
D. Sur
13. Dos ángulos son: complementarios si suman 90° y suplementario si suman 180°.
A. 40° y 50° son complementarios.
B. 40° y 50° son rectos.
C. 40° y 50° son suplementarios.
D. 40° y 50° son obtusos.
14. 150° y 30° son ángulos:
A. Suplementarios
B. Agudos
C. Rectos
D. Complementarios
15. Si un ángulo mide 60°, su complementario y su suplementario son respectivamente:
A. 30° y 90°
B. 30° y 60°
C. 30° y 120°
D. 90° y 120°
16. La región del plano limitada por tres o más segmentos concatenados se denomina:
A. Ángulo
B. Vértice
C. Lado
D. Polígono
17. Los segmentos que forman un polígono se llaman:
A. Vértices
B. Polígonos
C. Ángulos
D. Lados
Responda las preguntas 18 al 21 de
acuerdo a la gráfica.
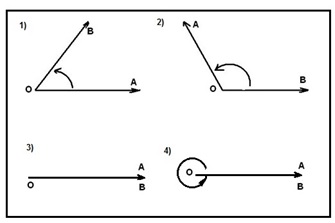
18. El ángulo de la figura 1 es:
A. Plano
B. Recto
C. Agudo
D. Nulo
19. El ángulo de la figura 2 es:
A. Obtuso
B. Recto
C. Agudo
D. Nulo
20. El ángulo de la figura 3 es:
A. Plano
B. Recto
C. Agudo
D. Nulo
21. El ángulo de la figura 4 es:
A. Plano
B. Recto
C. Agudo
D. Nulo
LA GEOMETRÍA Y LA EDUCACIÓN VÍAL
Actividad 3:
Leer y desarrollar los ejercicios de la siguiente guía:
HETEROEVALUACIÓN:
La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad: