Grado 10 - Trigonometría
Tercer Periodo
CONOCIMIENTOS PREVIOS: ÁNGULOS
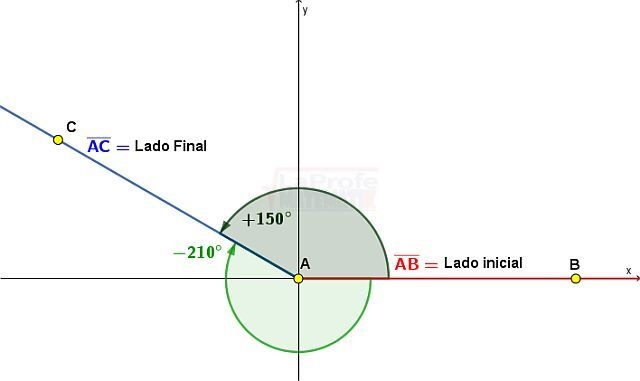
Recuerda: Si se parte del lado inicial y se gira en sentido contrario al movimiento de las manecillas
del reloj hasta llegar al lado final, se dice que la medida del ángulo es de signo positivo,
pero si el giro es el mismo sentido del movimiento de las manecillas del reloj, se
determina que la medida del ángulo es negativa.

Cuando en dos ángulos coinciden su lado inicial y el lado terminal se les denomina
coterminales, así como lo muestra la figura:
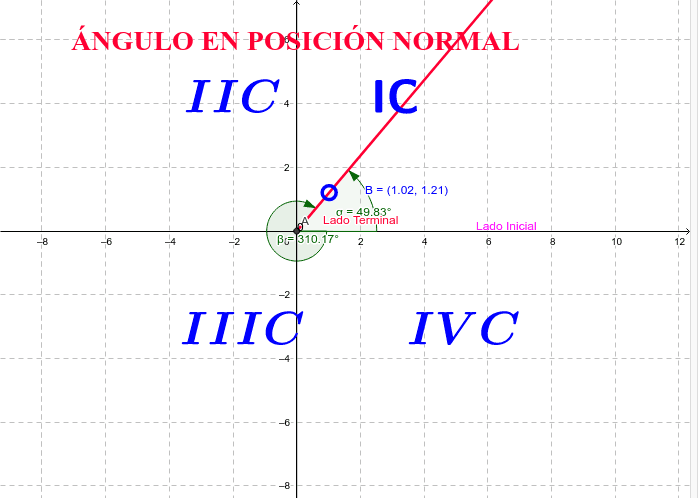
Cuando el ángulo se encuentra en un sistema de coordenadas y además el vértice
coincide con el origen del sistema y el lado inicial coincide con el semieje positivo de x,
se dice que el ángulo esta en posición normar o estándar.
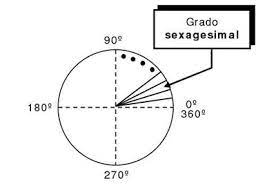
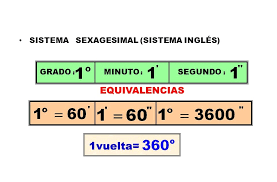
Recordemos que un ángulo es la porción de plano limitada por dos semirrectas que
tienen un origen común. Las unidades que más frecuentemente se utilizan para medir
ángulos son el grado y el radián.



Radianes:

El radián es independiente del radio de la circunferencia:
1. Si el radio de la circunferencia es 2 cm, el arco correspondiente al radián mide 2 cm.
2. Si el radio de otra circunferencia concéntrica es 4 cm, el arco correspondiente al radián medirá 4 cm.
Los sectores son semejantes y, por tanto, el ángulo central igual.
El ángulo completo, 360º, abarca toda la circunferencia, luego su media es 2Pi radianes,
que es precisamente la medida de la circunferencia cuando se toma como unidad el
radio. Por tanto, para pasar de grados a radianes, o al revés, basta con recordar que
360° grados = 2Pi radianes, y con una sencilla regla de tres es suficiente:

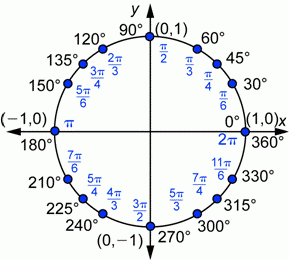
Ejemplo1: Veamos el manejo de la fórmula para convertir 243° a radianes:
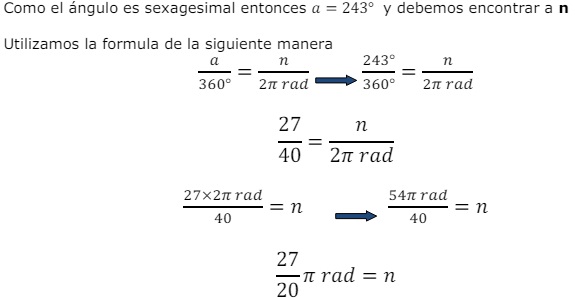
Ejemplo2:
Ejercicios 1:
De acuerdo a la fórmula de conversión, desarrolla los ejercicios que se encuentran en el siguiente enlace: https://www.liveworksheets.com/w/es/matematicas/714331
Cópialos en tu cuaderno y preséntalos al docente.
Función Seno - Coseno
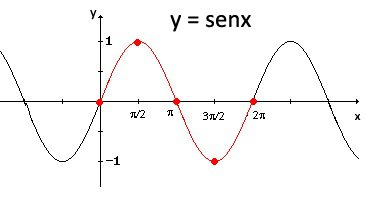
La función seno es una función periódica que es muy importante en trigonometría.
La forma más simple de entender la función seno es usar la unidad círculo. Para una medida de ángulo dado θ , dibuje una unidad círculo en el plano coordenado y dibuje el ángulo centrado al origen, con un lado en el eje positivo de las X . La coordenada en Y del punto donde el otro lado del ángulo intersecta al círculo es sin θ , y la coordenada en x es cos θ .
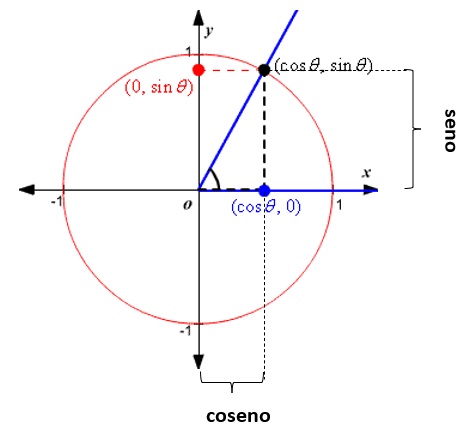
Ejemplo: Para que entiendas lo que acabo de decir voy a darte el siguiente ejemplo:
Hallar el seno y coseno de 30°
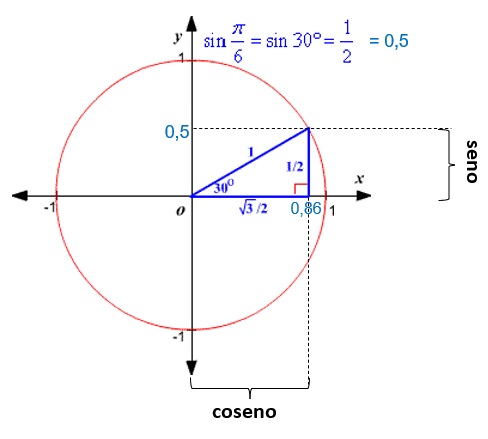
Nos damos cuenta que el seno de 30° es 0,8 que se ubica sobre el eje de las Y y el coseno de 30 es 0,86 que se ubica sobre el eje de las X, el radio es unitario es decir igual a 1.
Nota: las funciones trigonométricas se trabajan en radianes ya que sus resultados son datos de los números reales y no en grados, se toma acá en grados para una mayor comprensión de los ejercicios.
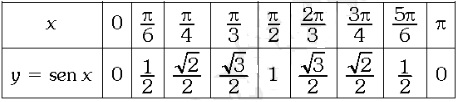
El dominio de la función y=sen X, son todos los números reales. En la siguiente tabla listamos algunos pares ordenados de dicha función. Nótese que los valores del dominio (x) están expresado en radianes y son ángulos especiales del I y II cuadrante de tal forma que los valores correspondientes de la imagen (y) son fáciles de calcular:
Ejercicio2: La mitad del grado va a dibujar la función seno en papel milimetrado, para realizar el ejercicio debes tener los siguientes elementos: Papel milimetrado, regla, transportador, curvígrafo, lápiz y borrador. La otra mitad del salón dibuja la función coseno, debe ser comparado en pareja el resultado y luego entregado al docente para su respectiva nota.
Para su elaboración vamos a observar el siguiente video:
Acá te doy una pequeña ayuda:
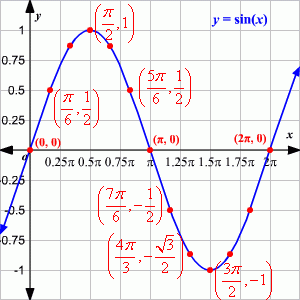
ELEMENTOS DE ANALISIS:
1. DOMINIO: el dominio es el conjunto de valores que puede tomar la variable (x) en el caso de la función F(x) = seno (x), es el conjunto de valores que toma el ángulo, es decir, el conjunto de números reales (R), ya que al ángulo se le puede dar cualquier valor real.

2. CODOMINIO: Son los valores de sen (x) que están en el intervalo [-1,1]

3. PUNTOS MAXIMOS: el punto máximo es la cresta más alta de una función, en el seno se encuentra en (π/2, 1)
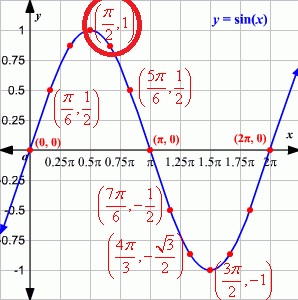
4. PUNTOS MINIMOS: el punto mínimo es la cresta más baja de una función, en el ejemplo del seno se encuentra en (3π/2, -1)
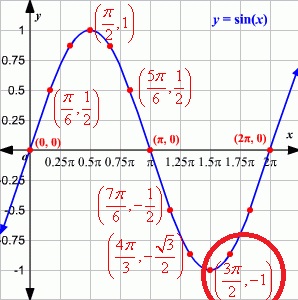
5. CEROS DE LA FUNCION: Se encuentran cuando en la función da 0, es decir cuando toca el eje x, para el ejemplo seno(x) = 0 da cero en: x=0, y=π,2π
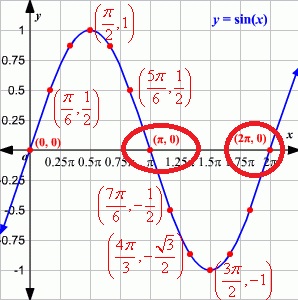
6. MONOTONIA: Intervalos donde crece o decrece la función; para nuestro ejemplo (función seno) es creciente en los intervalos [0, π/2] y [3/2π, 2π] Decrece en el intervalo [π/2, 3π/2].
7. SIMETRIA: La función f(x) = sen (x) es impar significa que sen (-x) = -sen (x). Es decir que su grafica no se altera luego de una rotación de π rad = 180°.
Ej: sen (-30)=-0.5 -sen(30)=-0.5
Es una función simétrica respecto del origen, esto significa que se refleja a lado del origen, como consecuencia por ser impar.
8. PERIODO: Es el valor de X a partir del cual se repiten los valores de f(x), en el caso de seno (x) el periodo es 2π es decir 360°.
9. CONTINUIDAD: Se refiere a que todos los valores del domino tienen una imagen en el codominio, por lo tanto, la gráfica no presenta rupturas ni huecos, es decir, es una línea continua.
10. AMPLITUD: es la distancia vertical entre el eje x y el punto máximo de la función (y), en el
caso de f(x) = sen (x) la amplitud es 1. Para determinar la amplitud de cualquier función se halla con la fórmula A = (valor máximo – valor mínimo) / 2
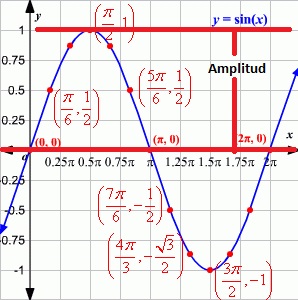
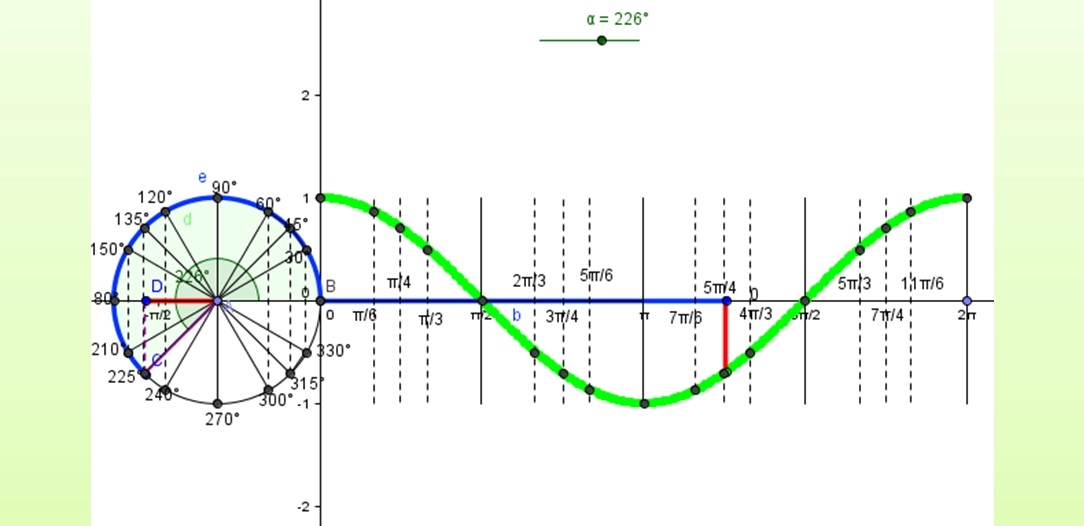
Ejercicio 3: Observe la gráfica que construyo usted o sus compañeros y complete los siguientes enunciados respecto de la función f(x) = Cos x
a. DOMINIO:
b. CODOMINIO:
c. PUNTOS MAXIMOS:
d. PUNTOS MINIMOS:
e. CEROS DE LA FUNCION:
f. MONOTONIA:
g. SIMETRÍA
h. PERIODO:
i. CONTINUIDAD:
j. AMPLITUD:
Función Tangente - Cotangente
Función Tangente:
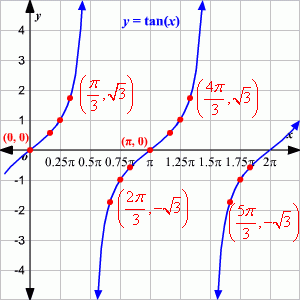
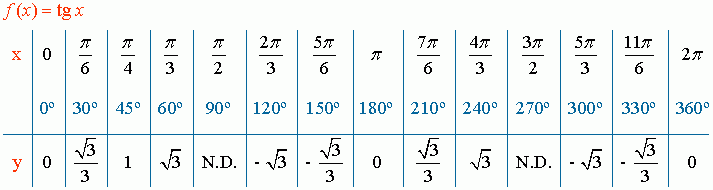
ANALISIS DE LA GRAFICA:
1. DOMINIO: Números reales menos los múltiplos impares de π/2 es decir, R – { (2n+1) π/2
2. CODOMINIO: Los números reales R
3. La función F(x) = tg x no tiene valores máximos ni mínimos, es decir no es acotada.
4. Los ceros de la función tg (x) se presentan en 0,π,2π.
5. La función tg(x) es una función periódica y su periodo es π, ya que después de se repiten sus valores.
6. La función tg (x) es una función impar pues se cumple tg(-X) = -tg(X)
7. Es una función discontinua ya que no está definida ND en π/2,3π/2
8. Presenta asíntotas verticales en todos los múltiplos de π/2 (Una asíntota es una recta que pasa por el punto donde se rompe la gráfica)
9. MONOTONIA: la función tg(X) es estrictamente creciente en todo su dominio.
Función cotangente:
Ejercicio 4:
1. Bajo las mismas consideraciones, utilizando los mismos ángulos de la tabla anterior, realice la tabla para y = Ctg (X) .
2. A partir de la tabla anterior construya la gráfica de Y = Ctg (X)
3. Analice la gráfica siguiendo el orden utilizado en la gráfica de tg(X)
4. Utilice las gráficas de las funciones tangente y cotangente para hallar los valores que hacen verdaderas las siguientes igualdades
a. tg (X) = 1 entonces X =_____________
b. tg(X) = 0 entonces X =_____________
c. tg(X) = √3 entonces X =_____________
d. Ctg(X) =-1 entonces X =_____________
e. Ctg(X) = 1 entonces X =_____________
f. Ctg(X)= 3/√3 entonces X =_____________
g. Tg(X) = ND entonces X =_____________
h. Ctg(X) =ND entonces X =_____________
5. Determine los signos de la función F(X) = Ctg (X) en los cuatro cuadrantes.
6. ¿Qué sucede con la gráfica de la función tangente cuando el valor de coseno es cero?
7. ¿Qué sucede con la gráfica de la función Cotangente cuando el valor de seno es cero?
8. ¿Qué sucede con la gráfica de la función tangente cuando el valor de seno es cero?
9. ¿Qué sucede con la gráfica de la función Cotangente cuando el valor de coseno es cero?
10. ¿Por qué la función cotangente tiene periodo π, si las funciones seno y coseno tienen
periodo 2π?
Función Secante - Cosecante
Función secante:
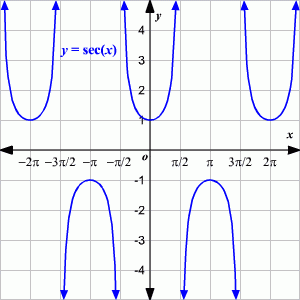
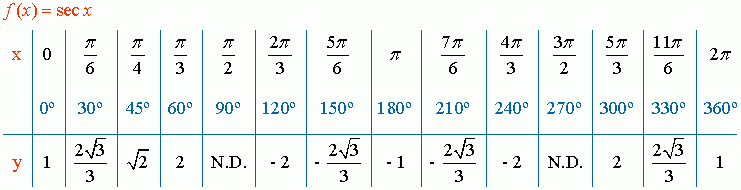
Ejercicio 5:
1. Construya la tabla, la gráfica y efectué el análisis de la función F(X) = Sec (X)
2. A partir de la gráfica de la función cosecante en el intervalo (-π, π), halle los valores de X que hacen verdaderas las siguientes igualdades.
a. Cesc X = 1 entonces X = _____________
b. Csc X = -1 entonces X = _____________
c. Csc X = √2 entonces X = _____________
d. Csc X = ND entonces X = _____________
e. Csc X < 0 entonces X = _____________
3. A partir de la gráfica de la función Secante en el intervalo (-π, π), halle los valores de X que hacen verdaderas las siguientes igualdades.
a. Sec X = 1 entonces X = _____________
b. Sec X = -1 entonces X = _____________
c. Sec X = √2 entonces X = _____________
d. Sec X = ND entonces X = _____________
e. Sec X < 0 entonces X = _____________
4. Determine si cada una de las siguientes afirmaciones es verdadera (V) o falsa (F). Justifique su respuesta.
a. Dominio de F(X) = Csc X es R
b. Dominio de Y= Sec (X) es R
c. La ecuación Sec (X) = 0 no tiene solución
d. La ecuación Csc (X) = 0 no tiene solución
e. La ecuación CSc (X) = 1 no tiene solución
f. El signo de la función F(X) = Sec X depende del signo de la función seno en cada cuadrante
Función cosecante:
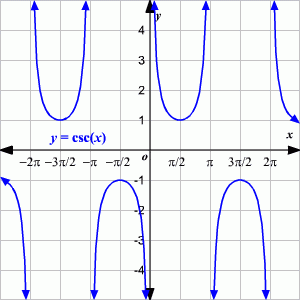
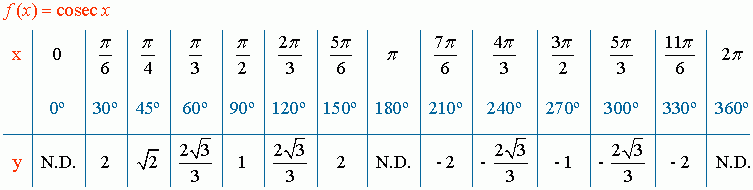
Ejercicio 6:
COMPLETE EL ANALISIS:
1. DOMINIO: R – {nπ}
2. CODOMINO: ____________
3. MONOTONIA_____________________
4. CEROS DE LA FUNCION_____________
5. PERIODO________________________
6. La función F(X) = Csc(X) es impar porque__________________
7. La función F(X) = Csc(X) no es acotada porque_____________
8. Las asíntotas de la función están en X= 0, π,2π…porque__________________
Identidades trigonométricas fundamentales
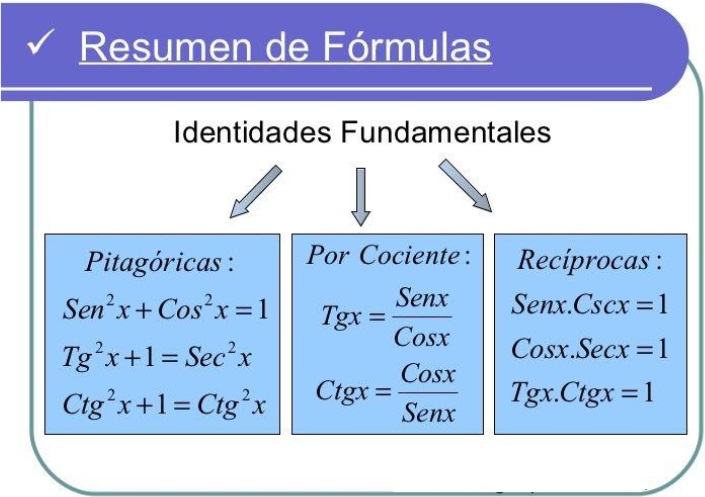
Conocimientos previos:

UNA IDENTIDAD ES UNA IGUALDAD QUE SE CUMPLE PARA TODOS LOS VALORES DE LA VARIABLE O INCOGNITA
Ahora se estudian las identidades trigonométricas que son transformaciones de expresiones
trigonométricas, a este proceso se llama demostración de una identidad.
Demostrar una identidad significa transformar uno de los miembros de la igualdad hasta
encontrar el otro, por medio de procesos sencillos como las operaciones básicas, factorización o
simple sustitución de identidades básicas
1. Identidad fundamental:
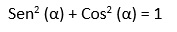
A partir del teorema de Pitágoras en el círculo
unitario podemos demostrar esta identidad.
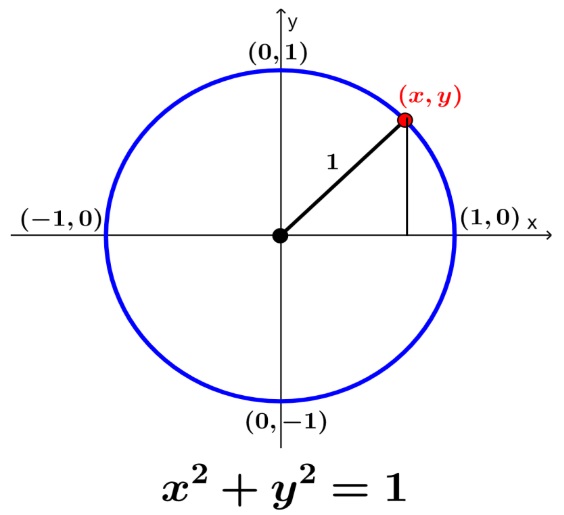
Recuerda que por el teorema de Pitágoras el cuadrado de la hipotenusa es igual a la suma del cuadrado de sus otros 2 catetos, esto ya se vio en periodos pasados, te invito a recordarlo a través del siguiente video:
x = COS α; y = Sen α, de acuerdo a lo visto en el capítulo de la función seno y coseno, entonces:
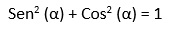
2. Identidades trigonométricas auxiliares:
Adicionalmente a las identidades fundamentales, se establecen una serie de relaciones
adicionales que se demuestran a partir de la primera. Van a destacar las siguientes relaciones:
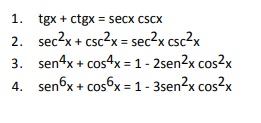
PASOS PARA DEMOSTRAR UNA IDENTIDAD
Aunque no existe una regla exacta que permita demostrar todas las identidades, hay algunas recomendaciones que siguiéndolas muy seguramente obtendrá un resultado positivo.
1. Inicie la demostración transformando el lado de la igualdad o miembro que permite mas operaciones, puede ser que parezca el más complejo.
2. Si es posible siempre busque expresar en términos de seno y coseno.
3. Utilizar formulas e identidades fundamentales, así como operaciones y factorizaciones básicas.
4. Tenga en cuenta la utilización de signos de agrupación si los hay.
5. Utilice los procesos correctos para efectuar operaciones con fracciones si es
necesario.
Ejemplos:

Ejercicio 7:
1. Simplifique cada una de las siguientes expresiones:

2. Escriba en términos de seno y coseno las siguientes expresiones:

3. Efectúe las operaciones indicadas;

4. Verifique con la demostración si las siguientes igualdades son identidades.
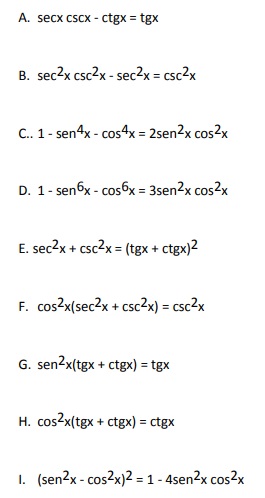
ECUACIONES TRIGONOMÉTRICAS
UNA ECUACION TRIGONOMETRICA ES UNA IGUALDAD QUE INVOLUCRA COMO VARIABLE UNA FUNCION TRIGONOMETRICA. Significa que la solución de la ecuación debe ser el valor del ángulo que hace verdadera dicha igualdad.
Teniendo en cuenta que las funciones trigonométricas son periódicas, la solución es el conjunto de
valores que satisfacen la igualdad inicial.
EJEMPLO1:
Resolver la ecuación Sen (x) +1 = 0
Iniciamos haciendo el despeje de la ecuación como normalmente se hace
Sen (x) = -1 y luego buscamos el valor del ángulo X para el cual el valor
de Sen(X) es -1, si miramos la gráfica o la tabla vemos que el ángulo X = 270° satisface la
ecuación:
Sen (270°) = -1
Ejercicio 8:
1. Resuelve las siguientes ecuaciones:
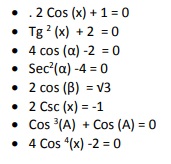
COORDENADAS POLARES
Antes de continuar con la explicación del tema te invito a observar el siguiente video:
Son un sistema de coordenadas bidimensional en el que cada punto del plano se determina por una distancia (r) y un ángulo (θ). Este sistema es ampliamente utilizado en física y trigonometría.

De manera más precisa, como sistema de referencia se toma: (a) un punto O del plano, al que se llama origen o polo; y (b) una recta dirigida (o rayo, o segmento OL) que pasa por O, llamada eje polar (equivalente al eje x del sistema cartesiano). Con este sistema de referencia y una unidad de medida métrica (para poder asignar distancias entre cada par de puntos del plano), todo punto P del plano corresponde a un par ordenado (r, θ) donde r es la distancia de P al origen y θ es el ángulo formado entre el eje polar y la recta dirigida OP que va de O a P.
El valor θ crece en sentido antihorario y decrece en sentido horario. La distancia r (r ≥ 0) se conoce como la «coordenada radial» o «radio vector», mientras que el ángulo es la «coordenada angular» o «ángulo polar».
En el caso del origen, O, el valor de r es cero, pero el valor de θ es indefinido. En ocasiones se adopta la convención de representar el origen por (0,0°).
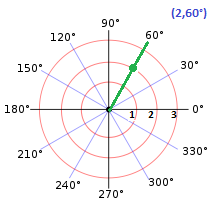
Ejemplo1:
Halla la coordenada polar (2,60°). En este caso nos vamos ayudar por círculos de uno en uno y grados de 30 en 30. Su resultado es el siguiente:
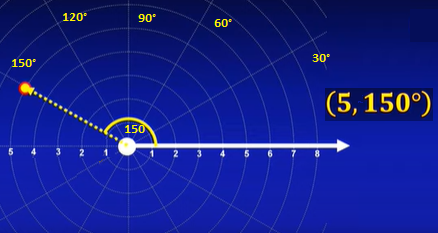
Ejemplo2:
Halla la coordenada polar (5,150°).
Ten en cuenta que la distancia r no es negativa, el que puede ser negativo es el radio:
Ejemplo3:
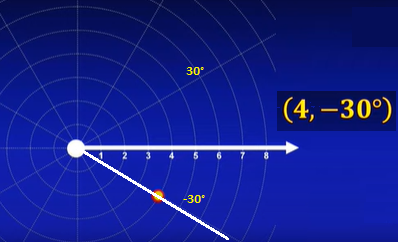
Halla la coordenada polar (4,-30°).
Recuerda que los ángulos negativos son los que van en la dirección de las manecillas del reloj, es decir hacia la derecha.
Ejemplo4:
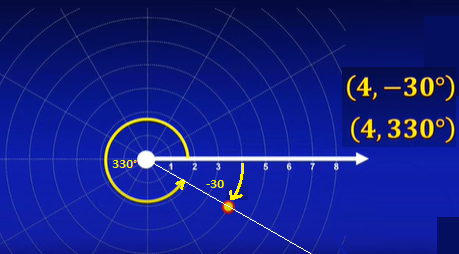
Halla la coordenada polar (4,330°).
Un mismo punto tiene infinitas coordenadas polares, en este ejempo es igual el punto (4,-30°) y (4,330°). Recuerda el tema "ángulos coterminales"
Nota: La única forma en que r sea negativa en una coordenada polar es cuando ya se ha determinado un ÁNGULO y el punto dado es contrario al rayo o r.
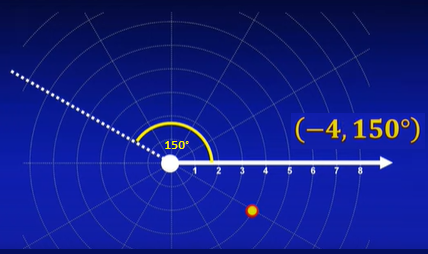
Ejemplo5:
Halla la coordenada polar (-4,150°).
Ejercicio 9:
Dibujar en papel milimetrado o en el cuaderno las siguientes coordenadas polares:
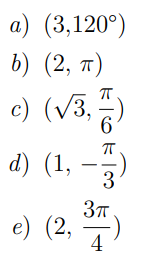
HETEROEVALUACIÓN: La valoración del trabajo desarrollado en la presente guía se realizará de la siguiente forma:
• Saber Hacer (50%):
a. Elaboración y entrega de las actividades propuestas.
b. Ejercicios de Prueba.
• Saber (25%):
a. Prueba Bimestral
• Ser - Convivir (25%):
a. Normas de Convivencia.
b. Responsabilidad y Cumplimiento en la entrega de trabajos.
c. Seguimiento a las instrucciones dadas por el docente.
d. Autoevaluación y Coevaluación.
AUTOEVALUACIÓN Y COEVALUACION:
Transcribir a hojas de block cuadriculado las siguientes tablas, marcar con una X en la casilla de la valoración correspondiente a los siguientes criterios y luego totalizar cada columna. Se debe realizar con la máxima sinceridad:
GUÍA DE APRENDIZAJE
En caso de no poseer internet, te invito a descargar la guía en el siguiente enlace:


